신경망(Neural Networks)

신경망은 torch.nn 패키지를 사용하여 생성할 수 있습니다.

지금까지 autograd 를 살펴봤는데요, nn 은 모델을 정의하고 미분하는데 autograd 를 사용합니다. nn.Module 은 계층(layer)과 output 을 반환하는 forward(input) 메서드를 포함하고 있습니다.

숫자 이미지를 분류하는 신경망을 예제로 살펴보겠습니다:

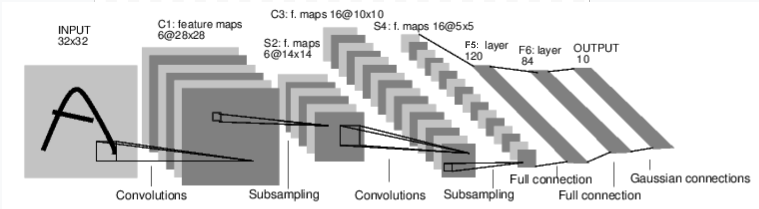
convnet

이는 간단한 순전파 네트워크(Feed-forward network)입니다. 입력(input)을 받아 여러 계층에 차례로 전달한 후, 최종 출력(output)을 제공합니다.

신경망의 일반적인 학습 과정은 다음과 같습니다:

• 학습 가능한 매개변수(또는 가중치(weight))를 갖는 신경망을 정의합니다.

• 데이터셋(dataset) 입력을 반복합니다.

• 입력을 신경망에서 전파(process)합니다.

• 손실(loss; 출력이 정답으로부터 얼마나 떨어져 있는지)을 계산합니다.

• 변화도(gradient)를 신경망의 매개변수들에 역으로 전파합니다.

• 신경망의 가중치를 갱신합니다. 일반적으로 다음과 같은 간단한 규칙을 사용합니다: 새로운 가중치(weight) = 가중치(weight) - 학습률(learning rate) * 변화도(gradient)

신경망 정의하기

이제 신경망을 정의해보겠습니다:

import torch
import torch.nn as nn
import torch.nn.functional as F


class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 입력 이미지 채널 1개, 출력 채널 6개, 5x5의 정사각 컨볼루션 행렬
        # 컨볼루션 커널 정의
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 아핀(affine) 연산: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)  # 5*5은 이미지 차원에 해당
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, input):
        # 합성곱(Convolution) 레이어 c1: 입력 이미지 채널 1, 출력 채널 6,
        # 5x5 정사각 합성곱, 활성 함수로 RELU 사용 및 (N, 6, 28, 28)의 크기를
        # 갖는 Tensor를 출력 (N은 배치 크기)
        c1 = F.relu(self.conv1(input))
        # 서브샘플링(Subsampling) 레이어 s2: 2x2 격자, 순전히 기능적인 레이어로,
        # 이 레이어는 어떠한 매개변수도 가지지 않고 (N, 6, 14, 14) Tensor를 출력
        s2 = F.max_pool2d(c1, (2, 2))
        # 합성곱(Convolution) 레이어 c3: 입력 채널 6, 출력 채널 16,
        # 5x5 정사각 합성곱, 활성 함수로 RELU 사용 및 (N, 16, 10, 10)의 크기를
        # 갖는 Tensor를 출력
        c3 = F.relu(self.conv2(s2))
        # 서브샘플링(Subsampling) 레이어 s4: 2x2 격자, 순전히 기능적인 레이어로,
        # 이 레이어는 어떠한 매개변수도 가지지 않고 (N, 16, 5, 5) Tensor를 출력
        s4 = F.max_pool2d(c3, 2)
        # 평탄화(flatten) 연산: 순전히 기능적으로 동작하며, (N, 400) Tensor를 출력
        s4 = torch.flatten(s4, 1)
        # 완전히 연결된 레이어 f5: (N, 400) Tensor를 입력으로 받아서
        # (N, 120) Tensor를 출력하며, 활성 함수로 RELU 사용
        f5 = F.relu(self.fc1(s4))
        # 완전히 연결된 레이어 f6: (N, 120) Tensor를 입력으로 받아서
        # (N, 84) Tensor를 출력하며, 활성 함수로 RELU 사용
        f6 = F.relu(self.fc2(f5))
        # 가우시안 레이어 출력: (N, 84) Tensor를 입력으로 받아서
        # (N, 10) Tensor를 출력
        output = self.fc3(f6)
        return output

    def forward(self, x):
        # (2, 2) 크기 윈도우에 대해 맥스 풀링(max pooling)
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 크기가 제곱수라면, 하나의 숫자만을 특정(specify)
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = torch.flatten(x, 1) # 배치 차원을 제외한 모든 차원을 하나로 평탄화(flatten)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

forward 함수만 정의하고 나면, (변화도를 계산하는) backward 함수는 autograd 를 사용하여 자동으로 정의됩니다. forward 함수에서는 어떠한 Tensor 연산을 사용해도 됩니다.

모델의 학습 가능한 매개변수들은 net.parameters() 에 의해 반환됩니다.

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1의 .weight

10
torch.Size([6, 1, 5, 5])

임의의 32x32 입력값을 넣어보겠습니다.

Note: 이 신경망(LeNet)의 예상되는 입력 크기는 32x32입니다. 이 신경망에 MNIST 데이터셋을 사용하기 위해서는, 데이터셋의 이미지 크기를 32x32로 변경해야 합니다.

input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

tensor([[ 0.1453, -0.0590, -0.0065,  0.0905,  0.0146, -0.0805, -0.1211, -0.0394,
         -0.0181, -0.0136]], grad_fn=<AddmmBackward0>)

모든 매개변수의 변화도 버퍼(gradient buffer)를 0으로 설정하고, 무작위 값으로 역전파를 합니다:

net.zero_grad()
out.backward(torch.randn(1, 10))

참고

torch.nn 은 미니배치(mini-batch)만 지원합니다. torch.nn 패키지 전체는 하나의 샘플이 아닌, 샘플들의 미니배치만을 입력으로 받습니다.

예를 들어, nnConv2D 는 nSamples x nChannels x Height x Width 의 4차원 Tensor를 입력으로 합니다.

만약 하나의 샘플만 있다면, input.unsqueeze(0) 을 사용해서 가상의 차원을 추가합니다.

계속 진행하기 전에, 지금까지 살펴봤던 것들을 다시 한번 요약해보겠습니다.

요약:

• torch.Tensor - backward() 같은 autograd 연산을 지원하는 다차원 배열 입니다. 또한 tensor에 대한 변화도를 갖고 있습니다.

• nn.Module - 신경망 모듈. 매개변수를 캡슐화(encapsulation)하는 간편한 방법 으로, GPU로 이동, 내보내기(exporting), 불러오기(loading) 등의 작업을 위한 헬퍼(helper)를 제공합니다.

• nn.Parameter - Tensor의 한 종류로, Module 에 속성으로 할당될 때 자동으로 매개변수로 등록 됩니다.

• autograd.Function - autograd 연산의 순방향과 역방향 정의 를 구현합니다. 모든 Tensor 연산은 하나 이상의 Function 노드를 생성하며, 각 노드는 Tensor 를 생성하고 이력(history)을 인코딩 하는 함수들과 연결하고 있습니다.

지금까지 우리가 다룬 내용은 다음과 같습니다:

• 신경망을 정의하는 것

• 입력을 처리하고 backward 를 호출하는 것

더 살펴볼 내용들은 다음과 같습니다:

• 손실을 계산하는 것

• 신경망의 가중치를 갱신하는 것

손실 함수 (Loss Function)

손실 함수는 (output, target)을 한 쌍(pair)의 입력으로 받아, 출력(output)이 정답(target)으로부터 얼마나 멀리 떨어져 있는지 추정하는 값을 계산합니다.

nn 패키지에는 여러가지의 손실 함수들 이 존재합니다. 간단한 손실 함수로는 출력과 대상간의 평균제곱오차(mean-squared error)를 계산하는 nn.MSEloss 가 있습니다.

예를 들면:

output = net(input)
target = torch.randn(10)  # 예시를 위한 임의의 정답
target = target.view(1, -1)  # 출력과 같은 shape로 만듦
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

tensor(1.3619, grad_fn=<MseLossBackward0>)

이제 .grad_fn 속성을 사용하여 loss 를 역방향에서 따라가다 보면, 이러한 모습의 연산 그래프를 볼 수 있습니다:

input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
      -> flatten -> linear -> relu -> linear -> relu -> linear
      -> MSELoss
      -> loss

따라서 loss.backward() 를 실행할 때, 전체 그래프는 신경망의 매개변수에 대해 미분되며, 그래프 내의 requires_grad=True 인 모든 Tensor는 변화도가 누적된 .grad Tensor를 갖게 됩니다.

설명을 위해, 역전파의 몇 단계를 따라가 보겠습니다:

print(loss.grad_fn)  # MSELoss
print(loss.grad_fn.next_functions[0][0])  # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0])  # ReLU

<MseLossBackward0 object at 0x778a9eac3d30>
<AddmmBackward0 object at 0x778a9eac2ce0>
<AccumulateGrad object at 0x778a9eac1c00>

역전파(Backprop)

오차(error)를 역전파하기 위해서는 loss.backward() 만 해주면 됩니다. 기존에 계산된 변화도의 값을 누적 시키고 싶지 않다면 기존에 계산된 변화도를 0으로 만드는 작업이 필요합니다.

이제 loss.backward() 를 호출하여 역전파 전과 후에 conv1의 bias 변수의 변화도를 살펴보겠습니다.

net.zero_grad()     # 모든 매개변수의 변화도 버퍼를 0으로 만듦

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
None
conv1.bias.grad after backward
tensor([ 0.0081, -0.0080, -0.0039,  0.0150,  0.0003, -0.0105])

지금까지 손실 함수를 어떻게 사용하는지를 살펴봤습니다.

더 읽어보기:

신경망 패키지(nn package)에는 심층 신경망(deep neural network)을 구성하는 다양한 모듈과 손실 함수가 포함되어 있습니다. 전체 목록은 이 문서 에 있습니다.

이제 더 살펴볼 내용은 다음과 같습니다:

• 신경망의 가중치를 갱신하는 것

가중치 갱신

실제로 많이 사용되는 가장 단순한 갱신 규칙은 확률적 경사하강법(SGD; Stochastic Gradient Descent)입니다:

# 새로운 가중치 = 가중치 - 학습률 * 변화도
weight = weight - learning_rate * gradient

간단한 Python 코드로 이를 구현해볼 수 있습니다:

learning_rate = 0.01
for f in net.parameters():
    f.data.sub_(f.grad.data * learning_rate)

신경망을 구성할 때 SGD, Nesterov-SGD, Adam, RMSProp 등과 같은 다양한 갱신 규칙을 사용하고 싶을 수 있습니다. 이를 위해서 torch.optim 라는 작은 패키지에 이러한 방법들을 모두 구현해두었습니다. 사용법은 매우 간단합니다:

import torch.optim as optim

# Optimizer를 생성합니다.
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 학습 과정(training loop)은 다음과 같습니다:
optimizer.zero_grad()   # 변화도 버퍼를 0으로
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # 업데이트 진행

참고

optimizer.zero_grad() 를 사용하여 수동으로 변화도 버퍼를 0으로 설정하는 것에 유의하세요. 이는 역전파(Backprop) 섹션에서 설명한 것처럼 변화도가 누적되기 때문입니다.