torch.autograd 에 대한 간단한 소개

torch.autograd 는 신경망 학습을 지원하는 PyTorch의 자동 미분 엔진입니다. 이 단원에서는 autograd가 신경망 학습을 어떻게 돕는지에 대한 개념적 이해를 할 수 있습니다.

배경(Background)

신경망(NN; Neural Network)은 어떤 입력 데이터에 대해 실행되는 중첩(nested)된 함수들의 모음(collection)입니다. 이 함수들은 PyTorch에서 Tensor로 저장되는, (가중치(weight)와 편향(bias)로 구성된) 매개변수들로 정의됩니다.

신경망을 학습하는 것은 2단계로 이루어집니다:

순전파(Forward Propagation): 순전파 단계에서, 신경망은 정답을 맞추기 위해 최선의 추측(best guess)을 합니다. 이렇게 추측을 하기 위해서 입력 데이터를 각 함수들에서 실행합니다.

역전파(Backward Propagation): 역전파 단계에서, 신경망은 추측한 값에서 발생한 오류(error)에 비례하여(proportionate) 매개변수들을 적절히 조절(adjust)합니다. 출력(output)로부터 역방향으로 이동하면서 오류에 대한 함수들의 매개변수들의 미분값( 변화도(gradient) )을 수집하고, 경사하강법(gradient descent)을 사용하여 매개변수들을 최적화 합니다. 역전파에 대한 자세한 설명은 3Blue1Brown의 비디오 를 참고하세요.

PyTorch에서 사용법

학습 단계를 하나만 살펴보겠습니다. 여기에서는 torchvision 에서 미리 학습된 resnet18 모델을 불러옵니다. 3채널짜리 높이와 넓이가 64인 이미지 하나를 표현하는 무작위의 데이터 텐서를 생성하고, 이에 상응하는 label(정답) 을 무작위 값으로 초기화합니다. 미리 학습된 모델의 정답(label)은 (1, 1000)의 모양(shape)을 갖습니다.

참고

이 튜토리얼은 (텐서를 CUDA로 이동하더라도) GPU에서는 동작하지 않으며 CPU에서만 동작합니다.

import torch
from torchvision.models import resnet18, ResNet18_Weights
model = resnet18(weights=ResNet18_Weights.DEFAULT)
data = torch.rand(1, 3, 64, 64)
labels = torch.rand(1, 1000)

다음으로, 입력(input) 데이터를 모델의 각 층(layer)에 통과시켜 예측값(prediction)을 생성해보겠습니다. 이것이 순전파 단계 입니다.

prediction = model(data) # 순전파 단계(forward pass)

모델의 예측값과 그에 해당하는 정답(label)을 사용하여 오차(error, 손실(loss) )를 계산합니다. 다음 단계는 신경망을 통해 이 에러를 역전파하는 것입니다. 오차 텐서(error tensor)에 .backward() 를 호출하면 역전파가 시작됩니다. 그 다음 Autograd가 매개변수(parameter)의 .grad 속성(attribute)에, 모델의 각 매개변수에 대한 변화도(gradient)를 계산하고 저장합니다.

loss = (prediction - labels).sum()
loss.backward() # 역전파 단계(backward pass)

다음으로, 옵티마이저(optimizer)를 불러옵니다. 이 예제에서는 학습률(learning rate) 0.1과 모멘텀(momentum) 0.9를 갖는 SGD입니다. 옵티마이저(optimizer)에 모델의 모든 매개변수를 등록합니다.

optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

마지막으로 .step 을 호출하여 경사하강법(gradient descent)을 시작합니다. 옵티마이저는 .grad 에 저장된 변화도에 따라 각 매개변수를 조정(adjust)합니다.

optim.step() # 경사하강법(gradient descent)

지금까지 신경망 학습에 필요한 모든 것을 알아보았습니다. 아래는 autograd의 동작에 대한 세부적인 내용을 설명하므로, 건너뛰어도 됩니다.

---

Autograd에서 미분(differentiation)

autograd 가 어떻게 변화도(gradient)를 수집하는지 살펴보겠습니다. requires_grad=True 를 갖는 2개의 텐서(tensor) a 와 b 를 만듭니다. requires_grad=True 는 autograd 에 모든 연산(operation)들을 추적해야 한다고 알려줍니다.

import torch

a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)

이제 a 와 b 로부터 새로운 텐서 Q 를 만듭니다 We create another tensor Q from a and b.

\[Q = 3a^3 - b^2 \]

Q = 3*a**3 - b**2

이제 a 와 b 가 모두 신경망(NN)의 매개변수이고, Q 가 오차(error)라고 가정해보겠습니다. 신경망을 학습할 때, 아래와 같이 매개변수들에 대한 오차의 변화도(gradient)를 구해야 합니다. 즉,

\[\frac{\partial Q}{\partial a} = 9a^2 \]

\[\frac{\partial Q}{\partial b} = -2b \]

Q 에 대해서 .backward() 를 호출할 때, autograd는 이러한 변화도들을 계산하고 이를 각 텐서의 .grad 속성(attribute)에 저장합니다.

Q 는 벡터(vector)이므로 Q.backward() 에 gradient 인자(argument)를 명시적으로 전달해야 합니다. gradient 는 Q 와 같은 모양(shape)의 텐서로, Q 자기 자신에 대한 변화도(gradient)를 나타냅니다. 즉

\[\frac{dQ}{dQ} = 1 \]

동일하게, Q.sum().backward() 와 같이 Q 를 스칼라(scalar) 값으로 집계(aggregate)한 뒤 암시적으로 .backward() 를 호출할 수도 있습니다.

external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

이제 변화도는 a.grad 와 b.grad 에 저장됩니다.

# 수집된 변화도가 올바른지 확인합니다.
print(9*a**2 == a.grad)
print(-2*b == b.grad)

tensor([True, True])
tensor([True, True])

선택적으로 읽기(Optional Reading) - autograd 를 사용한 벡터 미적분(calculus)

수학적으로, 벡터 함수 \(\vec{y}=f(\vec{x})\) 에서 \(\vec{x}\) 에 대한 \(\vec{y}\) 의 변화도는 야코비안 행렬(Jacobian Matrix) \(J\): 입니다:

\[J = \left(\begin{array}{cc} \frac{\partial \bf{y}}{\partial x_{1}} & ... & \frac{\partial \bf{y}}{\partial x_{n}} \end{array}\right) = \left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

일반적으로, torch.autograd 는 벡터-야코비안 곱을 계산하는 엔진입니다. 이는, 주어진 어떤 벡터 \(\vec{v}\) 에 대해 \(J^{T}\cdot \vec{v}\) 을 연산합니다.

만약 \(\vec{v}\) 가 스칼라 함수 \(l=g\left(\vec{y}\right)\) 의 변화도(gradient)인 경우:

\[\vec{v} = \left(\begin{array}{ccc}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)^{T}\]

이며, 연쇄 법칙(chain rule)에 따라, 벡터-야코비안 곱은 \(\vec{x}\) 에 대한 \(l\) 의 변화도(gradient)가 됩니다:

\[J^{T}\cdot \vec{v}=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{1}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{1}}{\partial x_{n}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\left(\begin{array}{c} \frac{\partial l}{\partial y_{1}}\\ \vdots\\ \frac{\partial l}{\partial y_{m}} \end{array}\right)=\left(\begin{array}{c} \frac{\partial l}{\partial x_{1}}\\ \vdots\\ \frac{\partial l}{\partial x_{n}} \end{array}\right)\]

위 예제에서 벡터-야코비안 곱의 이러한 특성을 사용했습니다; external_grad 가 \(\vec{v}\) 를 뜻합니다.

연산 그래프(Computational Graph)

개념적으로, autograd는 데이터(텐서)의 및 실행된 모든 연산들(및 연산 결과가 새로운 텐서인 경우도 포함하여)의 기록을 Function 객체로 구성된 방향성 비순환 그래프(DAG; Directed Acyclic Graph)에 저장(keep)합니다. 이 방향성 비순환 그래프(DAG)의 잎(leave)은 입력 텐서이고, 뿌리(root)는 결과 텐서입니다. 이 그래프를 뿌리에서부터 잎까지 추적하면 연쇄 법칙(chain rule)에 따라 변화도를 자동으로 계산할 수 있습니다.

순전파 단계에서, autograd는 다음 두 가지 작업을 동시에 수행합니다:

• 요청된 연산을 수행하여 결과 텐서를 계산하고,

• DAG에 연산의 변화도 기능(gradient function) 를 유지(maintain)합니다.

역전파 단계는 DAG 뿌리(root)에서 .backward() 가 호출될 때 시작됩니다. autograd 는 이 때:

• 각 .grad_fn 으로부터 변화도를 계산하고,

• 각 텐서의 .grad 속성에 계산 결과를 쌓고(accumulate),

• 연쇄 법칙을 사용하여, 모든 잎(leaf) 텐서들까지 전파(propagate)합니다.

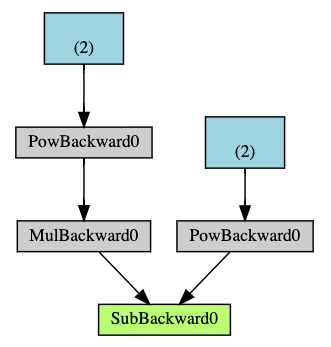
다음은 지금까지 살펴본 예제의 DAG를 시각적으로 표현한 것입니다. 그래프에서 화살표는 순전파 단계의 방향을 나타냅니다. 노드(node)들은 순전파 단계에서의 각 연산들에 대한 역전파 함수들을 나타냅니다. 파란색 잎(leaf) 노드는 잎 텐서 a 와 b 를 나타냅니다.

참고

PyTorch에서 DAG들은 동적(dynamic)입니다. 주목해야 할 중요한 점은 그래프가 처음부터(from scratch) 다시 생성된다는 것입니다; 매번 .backward() 가 호출되고 나면, autograd는 새로운 그래프를 채우기(populate) 시작합니다. 이러한 점 덕분에 모델에서 흐름 제어(control flow) 구문들을 사용할 수 있게 되는 것입니다; 매번 반복(iteration)할 때마다 필요하면 모양(shape)이나 크기(size), 연산(operation)을 바꿀 수 있습니다.

DAG에서 제외하기

torch.autograd 는 requires_grad 플래그(flag)가 True 로 설정된 모든 텐서에 대한 연산들을 추적합니다. 따라서 변화도가 필요하지 않은 텐서들에 대해서는 이 속성을 False 로 설정하여 DAG 변화도 계산에서 제외합니다.

입력 텐서 중 단 하나라도 requres_grad=True 를 갖는 경우, 연산의 결과 텐서도 변화도를 갖게 됩니다.

x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)

a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients?: {b.requires_grad}")

Does `a` require gradients? : False
Does `b` require gradients?: True

신경망에서, 변화도를 계산하지 않는 매개변수를 일반적으로 고정된 매개변수(frozen parameter) 이라고 부릅니다. 이러한 매개변수의 변화도가 필요하지 않다는 것을 미리 알고 있으면, 신경망 모델의 일부를 《고정(freeze)》하는 것이 유용합니다. (이렇게 하면 autograd 연산량을 줄임으로써 성능 상의 이득을 제공합니다.)

미세조정(finetuning)을 하는 과정에서, 새로운 정답(label)을 예측할 수 있도록 모델의 대부분을 고정한 뒤 일반적으로 분류 계층(classifier layer)만 변경합니다. 이를 설명하기 위해 간단한 예제를 살펴보겠습니다. 이전과 마찬가지로 이미 학습된 resnet18 모델을 불러온 뒤 모든 매개변수를 고정합니다.

from torch import nn, optim

model = resnet18(weights=ResNet18_Weights.DEFAULT)

# 신경망의 모든 매개변수를 고정합니다
for param in model.parameters():
    param.requires_grad = False

10개의 정답(label)을 갖는 새로운 데이터셋으로 모델을 미세조정하는 상황을 가정해보겠습니다. resnet에서 분류기(classifier)는 마지막 선형 계층(linear layer)인 model.fc 입니다. 이를 새로운 분류기로 동작할 (고정되지 않은) 새로운 선형 계층으로 간단히 대체하겠습니다.

model.fc = nn.Linear(512, 10)

이제 model.fc 를 제외한 모델의 모든 매개변수들이 고정되었습니다. 변화도를 계산하는 유일한 매개변수는 model.fc 의 가중치(weight)와 편향(bias)뿐입니다.

# 분류기만 최적화합니다.
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)

옵티마이저(optimizer)에 모든 매개변수를 등록하더라도, 변화도를 계산(하고 경사하강법으로 갱신)할 수 있는 매개변수들은 분류기의 가중치와 편향뿐입니다.

컨텍스트 매니저(context manager)에 torch.no_grad() 로도 똑같이 제외하는 기능을 사용할 수 있습니다.

---

더 읽어보기:

• In-place operations & Multithreaded Autograd

• Example implementation of reverse-mode autodiff