챗봇 튜토리얼

Author: Matthew Inkawhich

번역: 김진현

이 튜토리얼에서는 순환(recurrent) 시퀀스 투 시퀀스(sequence-to-sequence) 모델의 재미있고 흥미로운 사용 예를 살펴보려 합니다. 간단한 챗봇을 학습해 볼 텐데, 사용할 데이터는 영화 대본으로 구성된 Cornell Movie-Dialogs(코넬 대학교의 영화 속 대화 말뭉치 데이터 입니다.

대화형 모델은 많은 사람들이 관심을 갖는 인공지능 분야의 연구 주제입니다. 고객 서비스와 관련된 활용, 온라인 헬프데스크 등 여러 상황에서 챗봇을 활용할 수 있습니다. 많은 챗봇이 검색 기반(retrieval-based) 모델을 사용하는데, 이는 특정한 형식을 갖춘 질문에 대해 미리 정해진 반응을 출력하는 방식입니다. 분야를 특정 회사의 IT 헬프데스크처럼 한정한다면 이러한 모델을 사용해도 충분합니다. 그러나 이런 모델은 좀 더 일반적인 상황에 활용할 수 있을 만큼 강력하진 않습니다. 기계를 학습시켜서 사람과 여러 주제에 대해 의미 있는 대화를 하게끔 하는 것은 아직 해결되지 않은 연구 주제입니다. 그러나 최근에 딥러닝이 유행하면서 여러 가지의 강력한 생성 모델이 등장했습니다. 그러한 모델의 한 예인 구글의 신경 대화 모델(Neural Conversational Model) 은 다중 도메인 대화 생성 모델(multi-domain generative conversational models) 분야에 있어서 큰 진전을 이루었습니다. 우리는 이 튜토리얼을 통해 이러한 모델을 PyTorch로 구현해보려 합니다.

> hello? (안녕하세요?)
Bot: hello . (안녕하세요.)
> where am I? (여긴 어디죠?)
Bot: you re in a hospital . (병원입니다.)
> who are you? (당신은 누구시죠?)
Bot: i m a lawyer . (변호사입니다.)
> how are you doing? (어떻게 지내세요?)
Bot: i m fine . (잘 지냅니다.)
> are you my friend? (당신은 제 친구인가요?)
Bot: no . (아뇨.)
> you're under arrest (당신을 체포하겠습니다)
Bot: i m trying to help you ! (난 당신을 도우려 하는 겁니다!)
> i'm just kidding (농담이었어요)
Bot: i m sorry . (미안하네요.)
> where are you from? (어디서 오셨어요?)
Bot: san francisco . (샌프란시스코요.)
> it's time for me to leave (전 이제 가봐야겠네요)
Bot: i know . (알겠습니다.)
> goodbye (안녕히 계세요)
Bot: goodbye . (안녕히 가세요.)

이 튜토리얼의 핵심 내용

• 코넬 대학교의 영화 속 대화 말뭉치 데이터셋 을 읽어오고 전처리합니다

• Luong의 어텐션(attention) 메커니즘 을 이용하여 sequence-to-sequence 모델을 구현합니다

• 미니배치를 이용하여 인코더와 디코더를 함께 학습합니다

• 탐욕적 탐색 기법(greedy-search)을 사용하는 디코더 모듈을 구현합니다

• 학습한 챗봇과 대화를 나눠 봅니다

감사의 글

이 튜토리얼은 다음 자료의 도움을 받아 작성하였습니다.

1. Yuan-Kuei Wu의 pytorch-chatbot 구현체: https://github.com/ywk991112/pytorch-chatbot

2. Sean Robertson의 practical-pytorch seq2seq-translation 예제: https://github.com/spro/practical-pytorch/tree/master/seq2seq-translation

3. FloydHub의 코넬 대학교의 영화 말뭉치 데이터 전처리 코드: https://github.com/floydhub/textutil-preprocess-cornell-movie-corpus

준비 단계

시작에 앞서, 여기 에서 ZIP 파일 형태의 데이터를 내려받고, 현재 디렉토리 아래에 data/ 라는 디렉토리를 만들어서 내려받은 데이터를 옮겨두시기 바랍니다.

그 다음에는, 몇 가지 필요한 도구들을 import 하겠습니다.

import torch
from torch.jit import script, trace
import torch.nn as nn
from torch import optim
import torch.nn.functional as F
import csv
import random
import re
import os
import unicodedata
import codecs
from io import open
import itertools
import math
import json


USE_CUDA = torch.cuda.is_available()
device = torch.device("cuda" if USE_CUDA else "cpu")

데이터 읽기 & 전처리하기

다음 단계는 데이터 파일의 형식을 재조정한 후, 우리가 작업하기 편한 구조로 읽어들이는 것입니다.

코넬 대학교의 영화 속 대화 말뭉치 데이터셋 은 영화 속 등장 인물의 대화가 풍부하게 포함된 데이터셋입니다.

• 영화 속 등장 인물 10,292 쌍이 대화를 220,579번 주고받습니다

• 영화 617개의 등장 인물 9,035명이 나옵니다

• 총 발화(utterance) 수는 304,713번입니다

이 데이터셋은 규모도 크고 내용도 다양하며, 격식체와 비격식체, 여러 시간대, 여러 감정 상태 등이 두루 포함되어 있습니다. 우리의 바람은 이러한 다양성으로 인해 모델이 견고해지는, 즉 모델이 여러 종류의 입력 및 질의에 잘 대응할 수 있게 되는 것입니다.

우선은 원본 데이터 파일을 몇 줄 살펴보면서 형식이 어떻게 되어있는지 살펴 보겠습니다.

corpus_name = "movie-corpus"
corpus = os.path.join("data", corpus_name)

def printLines(file, n=10):
    with open(file, 'rb') as datafile:
        lines = datafile.readlines()
    for line in lines[:n]:
        print(line)

printLines(os.path.join(corpus, "utterances.jsonl"))

b'{"id": "L1045", "conversation_id": "L1044", "text": "They do not!", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "not", "tag": "RB", "dep": "neg", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L1044", "timestamp": null, "vectors": []}\n'
b'{"id": "L1044", "conversation_id": "L1044", "text": "They do to!", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "They", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "to", "tag": "TO", "dep": "dobj", "up": 1, "dn": []}, {"tok": "!", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L985", "conversation_id": "L984", "text": "I hope so.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "hope", "tag": "VBP", "dep": "ROOT", "dn": [0, 2, 3]}, {"tok": "so", "tag": "RB", "dep": "advmod", "up": 1, "dn": []}, {"tok": ".", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": "L984", "timestamp": null, "vectors": []}\n'
b'{"id": "L984", "conversation_id": "L984", "text": "She okay?", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 1, "toks": [{"tok": "She", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "okay", "tag": "RB", "dep": "ROOT", "dn": [0, 2]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L925", "conversation_id": "L924", "text": "Let\'s go.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Let", "tag": "VB", "dep": "ROOT", "dn": [2, 3]}, {"tok": "\'s", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "go", "tag": "VB", "dep": "ccomp", "up": 0, "dn": [1]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L924", "timestamp": null, "vectors": []}\n'
b'{"id": "L924", "conversation_id": "L924", "text": "Wow", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Wow", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L872", "conversation_id": "L870", "text": "Okay -- you\'re gonna need to learn how to lie.", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 4, "toks": [{"tok": "Okay", "tag": "UH", "dep": "intj", "up": 4, "dn": []}, {"tok": "--", "tag": ":", "dep": "punct", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "\'re", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "gon", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 2, 3, 6, 12]}, {"tok": "na", "tag": "TO", "dep": "aux", "up": 6, "dn": []}, {"tok": "need", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 8]}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 8, "dn": []}, {"tok": "learn", "tag": "VB", "dep": "xcomp", "up": 6, "dn": [7, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 11, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 11, "dn": []}, {"tok": "lie", "tag": "VB", "dep": "xcomp", "up": 8, "dn": [9, 10]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": "L871", "timestamp": null, "vectors": []}\n'
b'{"id": "L871", "conversation_id": "L870", "text": "No", "speaker": "u2", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "No", "tag": "UH", "dep": "ROOT", "dn": []}]}]}, "reply-to": "L870", "timestamp": null, "vectors": []}\n'
b'{"id": "L870", "conversation_id": "L870", "text": "I\'m kidding.  You know how sometimes you just become this \\"persona\\"?  And you don\'t know how to quit?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 2, "toks": [{"tok": "I", "tag": "PRP", "dep": "nsubj", "up": 2, "dn": []}, {"tok": "\'m", "tag": "VBP", "dep": "aux", "up": 2, "dn": []}, {"tok": "kidding", "tag": "VBG", "dep": "ROOT", "dn": [0, 1, 3]}, {"tok": ".", "tag": ".", "dep": "punct", "up": 2, "dn": [4]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 3, "dn": []}]}, {"rt": 1, "toks": [{"tok": "You", "tag": "PRP", "dep": "nsubj", "up": 1, "dn": []}, {"tok": "know", "tag": "VBP", "dep": "ROOT", "dn": [0, 6, 11]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 3, "dn": []}, {"tok": "sometimes", "tag": "RB", "dep": "advmod", "up": 6, "dn": [2]}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 6, "dn": []}, {"tok": "just", "tag": "RB", "dep": "advmod", "up": 6, "dn": []}, {"tok": "become", "tag": "VBP", "dep": "ccomp", "up": 1, "dn": [3, 4, 5, 9]}, {"tok": "this", "tag": "DT", "dep": "det", "up": 9, "dn": []}, {"tok": "\\"", "tag": "``", "dep": "punct", "up": 9, "dn": []}, {"tok": "persona", "tag": "NN", "dep": "attr", "up": 6, "dn": [7, 8, 10]}, {"tok": "\\"", "tag": "\'\'", "dep": "punct", "up": 9, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 1, "dn": [12]}, {"tok": " ", "tag": "_SP", "dep": "", "up": 11, "dn": []}]}, {"rt": 4, "toks": [{"tok": "And", "tag": "CC", "dep": "cc", "up": 4, "dn": []}, {"tok": "you", "tag": "PRP", "dep": "nsubj", "up": 4, "dn": []}, {"tok": "do", "tag": "VBP", "dep": "aux", "up": 4, "dn": []}, {"tok": "n\'t", "tag": "RB", "dep": "neg", "up": 4, "dn": []}, {"tok": "know", "tag": "VB", "dep": "ROOT", "dn": [0, 1, 2, 3, 7, 8]}, {"tok": "how", "tag": "WRB", "dep": "advmod", "up": 7, "dn": []}, {"tok": "to", "tag": "TO", "dep": "aux", "up": 7, "dn": []}, {"tok": "quit", "tag": "VB", "dep": "xcomp", "up": 4, "dn": [5, 6]}, {"tok": "?", "tag": ".", "dep": "punct", "up": 4, "dn": []}]}]}, "reply-to": null, "timestamp": null, "vectors": []}\n'
b'{"id": "L869", "conversation_id": "L866", "text": "Like my fear of wearing pastels?", "speaker": "u0", "meta": {"movie_id": "m0", "parsed": [{"rt": 0, "toks": [{"tok": "Like", "tag": "IN", "dep": "ROOT", "dn": [2, 6]}, {"tok": "my", "tag": "PRP$", "dep": "poss", "up": 2, "dn": []}, {"tok": "fear", "tag": "NN", "dep": "pobj", "up": 0, "dn": [1, 3]}, {"tok": "of", "tag": "IN", "dep": "prep", "up": 2, "dn": [4]}, {"tok": "wearing", "tag": "VBG", "dep": "pcomp", "up": 3, "dn": [5]}, {"tok": "pastels", "tag": "NNS", "dep": "dobj", "up": 4, "dn": []}, {"tok": "?", "tag": ".", "dep": "punct", "up": 0, "dn": []}]}]}, "reply-to": "L868", "timestamp": null, "vectors": []}\n'

원하는 형식의 데이터 파일로 만들기

편의를 위해 데이터의 형식을 원하는 형태로 만들려고 합니다. 각 줄에 질의 문장 과 응답 문장 의 쌍이 탭으로 구분되어 있게끔 하는 것입니다.

다음의 함수를 통해 utterances.jsonl 원본 데이터 파일을 파싱하려 합니다.

• loadLines 는 파일에 포함된 대사를 변환하여 항목(대사 ID lineID, 인물 ID characterID, 영화 ID movieID, 인물 character, 대사 내용 text)에 대한 사전 형태로 변환합니다

• loadConversations 는 loadLines 를 통해 읽어들인 대사( lines )의 항목( fields )를 movie_conversations.txt 에 나와 있는 내용에 맞춰 대화 형태로 묶습니다

• extractSentencePairs 는 대화( conversations )에서 문장 쌍을 추출합니다

# 파일에 포함된 각 줄을 쪼개서 대사(line)와 대화(conversation)를 생성합니다.
def loadLinesAndConversations(fileName):
    lines = {}
    conversations = {}
    with open(fileName, 'r', encoding='iso-8859-1') as f:
        for line in f:
            lineJson = json.loads(line)
            # 필드를 추출하여 line 객체를 구성합니다
            lineObj = {}
            lineObj["lineID"] = lineJson["id"]
            lineObj["characterID"] = lineJson["speaker"]
            lineObj["text"] = lineJson["text"]
            lines[lineObj['lineID']] = lineObj

            # 필드를 추출하여 conversation 객체를 구성합니다
            if lineJson["conversation_id"] not in conversations:
                convObj = {}
                convObj["conversationID"] = lineJson["conversation_id"]
                convObj["movieID"] = lineJson["meta"]["movie_id"]
                convObj["lines"] = [lineObj]
            else:
                convObj = conversations[lineJson["conversation_id"]]
                convObj["lines"].insert(0, lineObj)
            conversations[convObj["conversationID"]] = convObj

    return lines, conversations

# conversation들에서 문장 쌍을 추출합니다
def extractSentencePairs(conversations):
    qa_pairs = []
    for conversation in conversations.values():
        # 대화를 이루는 각 대사에 대해 반복문을 수행합니다
        # 대화의 마지막 대사는 (그에 대한 응답이 없으므로) 무시합니다
        for i in range(len(conversation["lines"]) - 1):
            inputLine = conversation["lines"][i]["text"].strip()
            targetLine = conversation["lines"][i+1]["text"].strip()
            # 잘못된 샘플은 제거합니다(리스트가 하나라도 비어 있는 경우)
            if inputLine and targetLine:
                qa_pairs.append([inputLine, targetLine])
    return qa_pairs

이제 이 함수들을 호출하여 새로운 파일인 formatted_movie_lines.txt 를 만듭니다.

# 새 파일에 대한 경로를 정의합니다
datafile = os.path.join(corpus, "formatted_movie_lines.txt")

delimiter = '\t'
# 구분자에 대해 unescape 함수를 호출합니다
delimiter = str(codecs.decode(delimiter, "unicode_escape"))

# 대사 사전(lines dict)과 대화 사전(conversations dict)을 초기화합니다
lines = {}
conversations = {}
# 대사와 대화를 불러옵니다
print("\nProcessing corpus into lines and conversations...")
lines, conversations = loadLinesAndConversations(os.path.join(corpus, "utterances.jsonl"))

# 결과를 새로운 csv 파일로 저장합니다
print("\nWriting newly formatted file...")
with open(datafile, 'w', encoding='utf-8') as outputfile:
    writer = csv.writer(outputfile, delimiter=delimiter, lineterminator='\n')
    for pair in extractSentencePairs(conversations):
        writer.writerow(pair)

# 몇 줄을 예제 삼아 출력해 봅니다
print("\nSample lines from file:")
printLines(datafile)

Processing corpus into lines and conversations...

Writing newly formatted file...

Sample lines from file:
b'They do to!\tThey do not!\n'
b'She okay?\tI hope so.\n'
b"Wow\tLet's go.\n"
b'"I\'m kidding.  You know how sometimes you just become this ""persona""?  And you don\'t know how to quit?"\tNo\n'
b"No\tOkay -- you're gonna need to learn how to lie.\n"
b"I figured you'd get to the good stuff eventually.\tWhat good stuff?\n"
b'What good stuff?\t"The ""real you""."\n'
b'"The ""real you""."\tLike my fear of wearing pastels?\n'
b'do you listen to this crap?\tWhat crap?\n'
b"What crap?\tMe.  This endless ...blonde babble. I'm like, boring myself.\n"

데이터 읽고 정리하기

다음에 해야 할 일은 어휘집을 만들고, 질의/응답 문장 쌍을 메모리로 읽어들이는 것입니다.

우리가 다루는 대상은 일련의 단어 들이며, 따라서 이들을 이산 공간 상의 수치(discrete numerical space)로 자연스럽게 대응시키기 어렵다는 점에 유의하시기 바랍니다. 따라서 우리는 데이터셋 안에 들어 있는 단어를 인덱스 값으로 변환하는 매핑을 따로 만들어야 합니다.

이를 위해 우리는 Voc 라는 클래스를 만들어 단어에서 인덱스로의 매핑, 인덱스에서 단어로의 역 매핑, 각 단어의 등장 횟수, 전체 단어 수 등을 관리하려 합니다. 이 클래스는 어휘집에 새로운 단어를 추가하는 메서드( addWord), 문장에 등장하는 모든 단어를 추가하는 메서드( addSentence), 그리고 자주 등장하지 않는 단어를 정리하는 메서드( trim)를 제공합니다. 단어를 정리하는 내용에 대해서는 뒤에서 좀 더 자세히 살펴보겠습니다.

# 기본 단어 토큰 값
PAD_token = 0  # 짧은 문장을 채울(패딩, PADding) 때 사용할 제로 토큰
SOS_token = 1  # 문장의 시작(SOS, Start Of Sentence)을 나타내는 토큰
EOS_token = 2  # 문장의 끝(EOS, End Of Sentence)을 나태는 토큰

class Voc:
    def __init__(self, name):
        self.name = name
        self.trimmed = False
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3  # SOS, EOS, PAD를 센 것

    def addSentence(self, sentence):
        for word in sentence.split(' '):
            self.addWord(word)

    def addWord(self, word):
        if word not in self.word2index:
            self.word2index[word] = self.num_words
            self.word2count[word] = 1
            self.index2word[self.num_words] = word
            self.num_words += 1
        else:
            self.word2count[word] += 1

    # 등장 횟수가 기준 이하인 단어를 정리합니다
    def trim(self, min_count):
        if self.trimmed:
            return
        self.trimmed = True

        keep_words = []

        for k, v in self.word2count.items():
            if v >= min_count:
                keep_words.append(k)

        print('keep_words {} / {} = {:.4f}'.format(
            len(keep_words), len(self.word2index), len(keep_words) / len(self.word2index)
        ))

        # 사전을 다시 초기화합니다
        self.word2index = {}
        self.word2count = {}
        self.index2word = {PAD_token: "PAD", SOS_token: "SOS", EOS_token: "EOS"}
        self.num_words = 3 # 기본 토큰을 센 것

        for word in keep_words:
            self.addWord(word)

이제 어휘집과 질의/응답 문장 쌍을 재구성하려 합니다. 그러한 데이터를 사용하려면 그 전에 약간의 전처리 작업을 수행해야 합니다.

우선, unicodeToAscii 를 이용하여 유니코드 문자열을 아스키로 변환해야 합니다. 다음에는 모든 글자를 소문자로 변환하고, 알파벳도 아니고 기본적인 문장 부호도 아닌 글자는 제거합니다(정규화, normalizeString). 마지막으로는 학습할 때의 편의성을 위해서, 길이가 일정 기준을 초과하는, 즉 MAX_LENGTH 보다 긴 문장을 제거합니다( filterPairs).

MAX_LENGTH = 10  # 고려할 문장의 최대 길이

# 유니코드 문자열을 아스키로 변환합니다
# https://stackoverflow.com/a/518232/2809427 참고
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
    )

# 소문자로 만들고, 공백을 넣고, 알파벳 외의 글자를 제거합니다
def normalizeString(s):
    s = unicodeToAscii(s.lower().strip())
    s = re.sub(r"([.!?])", r" \1", s)
    s = re.sub(r"[^a-zA-Z.!?]+", r" ", s)
    s = re.sub(r"\s+", r" ", s).strip()
    return s

# 질의/응답 쌍을 읽어서 voc 객체를 반환합니다
def readVocs(datafile, corpus_name):
    print("Reading lines...")
    # 파일을 읽고, 쪼개어 lines에 저장합니다
    lines = open(datafile, encoding='utf-8').\
        read().strip().split('\n')
    # 각 줄을 쪼개어 pairs에 저장하고 정규화합니다
    pairs = [[normalizeString(s) for s in l.split('\t')] for l in lines]
    voc = Voc(corpus_name)
    return voc, pairs

# 문장의 쌍 'p'에 포함된 두 문장이 모두 MAX_LENGTH라는 기준보다 짧은지를 반환합니다
def filterPair(p):
    # EOS 토큰을 위해 입력 시퀀스의 마지막 단어를 보존해야 합니다
    return len(p[0].split(' ')) < MAX_LENGTH and len(p[1].split(' ')) < MAX_LENGTH

# 조건식 ``filterPair`` 에 따라 pairs를 필터링합니다
def filterPairs(pairs):
    return [pair for pair in pairs if filterPair(pair)]

# 앞에서 정의한 함수를 이용하여 만든 voc 객체와 리스트 pairs를 반환합니다
def loadPrepareData(corpus, corpus_name, datafile, save_dir):
    print("Start preparing training data ...")
    voc, pairs = readVocs(datafile, corpus_name)
    print("Read {!s} sentence pairs".format(len(pairs)))
    pairs = filterPairs(pairs)
    print("Trimmed to {!s} sentence pairs".format(len(pairs)))
    print("Counting words...")
    for pair in pairs:
        voc.addSentence(pair[0])
        voc.addSentence(pair[1])
    print("Counted words:", voc.num_words)
    return voc, pairs


# voc와 pairs를 읽고 재구성합니다
save_dir = os.path.join("data", "save")
voc, pairs = loadPrepareData(corpus, corpus_name, datafile, save_dir)
# 검증을 위해 pairs의 일부 내용을 출력해 봅니다
print("\npairs:")
for pair in pairs[:10]:
    print(pair)

Start preparing training data ...
Reading lines...
Read 221282 sentence pairs
Trimmed to 64313 sentence pairs
Counting words...
Counted words: 18082

pairs:
['they do to !', 'they do not !']
['she okay ?', 'i hope so .']
['wow', 'let s go .']
['what good stuff ?', 'the real you .']
['the real you .', 'like my fear of wearing pastels ?']
['do you listen to this crap ?', 'what crap ?']
['well no . . .', 'then that s all you had to say .']
['then that s all you had to say .', 'but']
['but', 'you always been this selfish ?']
['have fun tonight ?', 'tons']

학습 단계가 빨리 수렴하도록 하는 또 다른 전략은 자주 쓰이지 않는 단어를 어휘집에서 제거하는 것입니다. 피처 공간의 크기를 줄이면 모델이 학습을 통해 근사하려는 함수의 난이도를 낮추는 효과도 있습니다. 우리는 이를 두 단계로 나눠 진행하려 합니다.

1. voc.trim 함수를 이용하여 MIN_COUNT 라는 기준 이하의 단어를 제거합니다.

2. 제거하기로 한 단어를 포함하는 경우를 pairs에서 제외합니다.

MIN_COUNT = 3    # 제외할 단어의 기준이 되는 등장 횟수

def trimRareWords(voc, pairs, MIN_COUNT):
    # MIN_COUNT 미만으로 사용된 단어는 voc에서 제외합니다
    voc.trim(MIN_COUNT)
    # 제외할 단어가 포함된 경우를 pairs에서도 제외합니다
    keep_pairs = []
    for pair in pairs:
        input_sentence = pair[0]
        output_sentence = pair[1]
        keep_input = True
        keep_output = True
        # 입력 문장을 검사합니다
        for word in input_sentence.split(' '):
            if word not in voc.word2index:
                keep_input = False
                break
        # 출력 문장을 검사합니다
        for word in output_sentence.split(' '):
            if word not in voc.word2index:
                keep_output = False
                break

        # 입출력 문장에 제외하기로 한 단어를 포함하지 않는 경우만을 남겨둡니다
        if keep_input and keep_output:
            keep_pairs.append(pair)

    print("Trimmed from {} pairs to {}, {:.4f} of total".format(len(pairs), len(keep_pairs), len(keep_pairs) / len(pairs)))
    return keep_pairs


# voc와 pairs를 정돈합니다
pairs = trimRareWords(voc, pairs, MIN_COUNT)

keep_words 7833 / 18079 = 0.4333
Trimmed from 64313 pairs to 53131, 0.8261 of total

모델을 위한 데이터 준비하기

상당한 노력을 기울여 데이터를 전처리하고, 잘 정리하여 어휘집 객체와 문장 쌍의 리스트 형태로 만들어두긴 했지만, 결국 우리가 만들 모델에서 사용하는 입력은 수치 값으로 이루어진 torch 텐서입니다. 처리한 데이터를 모델에 맞는 형태로 준비하는 방법의 하나가 seq2seq 변환 튜토리얼 에 나와 있습니다. 이 튜토리얼에서는 배치 크기로 1을 사용하며, 이는 즉 문장에 등장하는 단어를 어휘집에서의 인덱스로 변환하여 모델에 제공하기만 하면 된다는 의미입니다.

그래도 여러분이 학습 속도나 GPU 병렬 처리 용량을 향상하고 싶다면 미니배치를 이용하여 학습해야 할 것입니다.

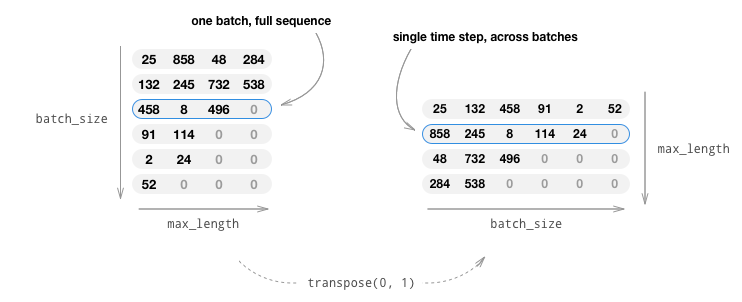
미니배치를 사용한다는 것은 배치에 포함된 문장 길이가 달라질 수 있다는 점에 유의해야 한다는 것을 뜻합니다. 같은 배치 안에서 크기가 다른 문장을 처리하기 위해서는 배치용 입력 텐서의 모양을 (max_length, batch_size) 로 맞춰야 합니다. 이때 max_length 보다 짧은 문장에 대해서는 EOS_token 뒤에 제로 토큰을 덧붙이면 됩니다.

영어로 된 문장을 텐서로 변환하기 위해 단순히 그에 대응하는 인덱스를 사용하고(indexesFromSentence) 제로 토큰을 패딩한다고 해봅시다. 그러면 텐서의 모양이 (batch_size, max_length) 이 되고, 첫 번째 차원에 대해 인덱싱을 수행하면 모든 시간대별 문장이 전부 반환될 것입니다. 그러나 우리는 배치를 시간에 따라, 그리고 배치에 포함된 모든 문장에 대해 인덱싱할 수도 있어야 합니다. 따라서 우리는 입력 배치의 모양을 뒤집어서 (max_length, batch_size) 형태로 만들 것입니다. 그러고 난 후에 첫 번째 차원에 대해 인덱싱하면 배치에 포함된 모든 문장을 시간에 대해 인덱싱한 결과를 반환하게 됩니다. 우리는 이 뒤집기 작업을 zeroPadding 함수를 이용하여 묵시적으로 수행할 것입니다.

inputVar 함수는 문장을 텐서로 변환하는, 그리고 궁극적으로는 제로 패딩하여 올바른 모양으로 맞춘 텐서를 만드는 작업을 수행합니다. 이 함수는 각 배치에 포함된 시퀀스의 길이(lengths)로 구성된 텐서도 같이 반환합니다. 그리고 우리는 이를 나중에 디코더로 넘겨줄 것입니다.

outputVar 함수는 inputVar 와 비슷한 작업을 수행하지만, lengths 텐서를 반환하는 대신에 이진 마스크로 구성된 텐서와 목표 문장의 최대 길이를 같이 반환합니다. 이진 마스크 텐서는 출력에 해당하는 목표 텐서와 그 모양이 같지만, 패딩 토큰( PAD_token )에 해당하는 경우에는 값이 0이며 나머지 경우의 값은 1입니다.

batch2TrainData 는 단순히 여러 쌍을 입력으로 받아서, 앞서 설명한 함수를 이용하여 입력 및 목표 텐서를 구하여 반환합니다.

def indexesFromSentence(voc, sentence):
    return [voc.word2index[word] for word in sentence.split(' ')] + [EOS_token]


def zeroPadding(l, fillvalue=PAD_token):
    return list(itertools.zip_longest(*l, fillvalue=fillvalue))

def binaryMatrix(l, value=PAD_token):
    m = []
    for i, seq in enumerate(l):
        m.append([])
        for token in seq:
            if token == PAD_token:
                m[i].append(0)
            else:
                m[i].append(1)
    return m

# 입력 시퀀스 텐서에 패딩한 결과와 lengths를 반환합니다
def inputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    padVar = torch.LongTensor(padList)
    return padVar, lengths

# 패딩한 목표 시퀀스 텐서, 패딩 마스크, 그리고 최대 목표 길이를 반환합니다
def outputVar(l, voc):
    indexes_batch = [indexesFromSentence(voc, sentence) for sentence in l]
    max_target_len = max([len(indexes) for indexes in indexes_batch])
    padList = zeroPadding(indexes_batch)
    mask = binaryMatrix(padList)
    mask = torch.BoolTensor(mask)
    padVar = torch.LongTensor(padList)
    return padVar, mask, max_target_len

# 입력 배치를 이루는 쌍에 대한 모든 아이템을 반환합니다
def batch2TrainData(voc, pair_batch):
    pair_batch.sort(key=lambda x: len(x[0].split(" ")), reverse=True)
    input_batch, output_batch = [], []
    for pair in pair_batch:
        input_batch.append(pair[0])
        output_batch.append(pair[1])
    inp, lengths = inputVar(input_batch, voc)
    output, mask, max_target_len = outputVar(output_batch, voc)
    return inp, lengths, output, mask, max_target_len


# 검증용 예시
small_batch_size = 5
batches = batch2TrainData(voc, [random.choice(pairs) for _ in range(small_batch_size)])
input_variable, lengths, target_variable, mask, max_target_len = batches

print("input_variable:", input_variable)
print("lengths:", lengths)
print("target_variable:", target_variable)
print("mask:", mask)
print("max_target_len:", max_target_len)

input_variable: tensor([[  86,   24,  140,  829,   62],
        [   6,  355, 1362,  206,  566],
        [  36,  735,   14,   72, 1919],
        [  17,  140,  140, 2160,   85],
        [  62,   28,  158,   14,   14],
        [1012,  461,  140,    2,    2],
        [3223,   10,   14,    0,    0],
        [1012,    2,    2,    0,    0],
        [   6,    0,    0,    0,    0],
        [   2,    0,    0,    0,    0]])
lengths: tensor([10,  8,  8,  6,  6])
target_variable: tensor([[  18,   11,  101,   93,  277],
        [ 483,  113,   19,  311,   72],
        [   5,  241,   10,   72,   10],
        [  22,  706,    2,   19,    2],
        [2010,   14,    0,   24,    0],
        [1556,    2,    0,  136,    0],
        [  14,    0,    0,    5,    0],
        [   2,    0,    0,   48,    0],
        [   0,    0,    0,   14,    0],
        [   0,    0,    0,    2,    0]])
mask: tensor([[ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True,  True,  True,  True],
        [ True,  True, False,  True, False],
        [ True,  True, False,  True, False],
        [ True, False, False,  True, False],
        [ True, False, False,  True, False],
        [False, False, False,  True, False],
        [False, False, False,  True, False]])
max_target_len: 10

모델 정의하기

Seq2Seq 모델

우리 챗봇의 두뇌에 해당하는 모델은 sequence-to-sequence (seq2seq) 모델입니다. seq2seq 모델의 목표는 가변 길이 시퀀스를 입력으로 받고, 크기가 고정된 모델을 이용하여, 가변 길이 시퀀스를 출력으로 반환하는 것입니다.

Sutskever 등 은 두 개의 독립된 순환 신경망을 같이 이용하여 이러한 목적을 달성할 수 있음을 발견했습니다. RNN 하나는 인코더 로, 가변 길이 입력 시퀀스를 고정된 길이의 문맥 벡터(context vector)로 인코딩합니다. 이론상 문맥 벡터(RNN의 마지막 은닉 레이어)는 봇에게 입력으로 주어지는 질의 문장에 대한 의미론적 정보를 담고 있을 것입니다. 두 번째 RNN은 디코더 입니다. 디코더는 단어 하나와 문맥 벡터를 입력으로 받고, 시퀀스의 다음 단어가 무엇일지를 추론하여 반환하며, 다음 단계에서 사용할 은닉 상태도 같이 반환합니다.

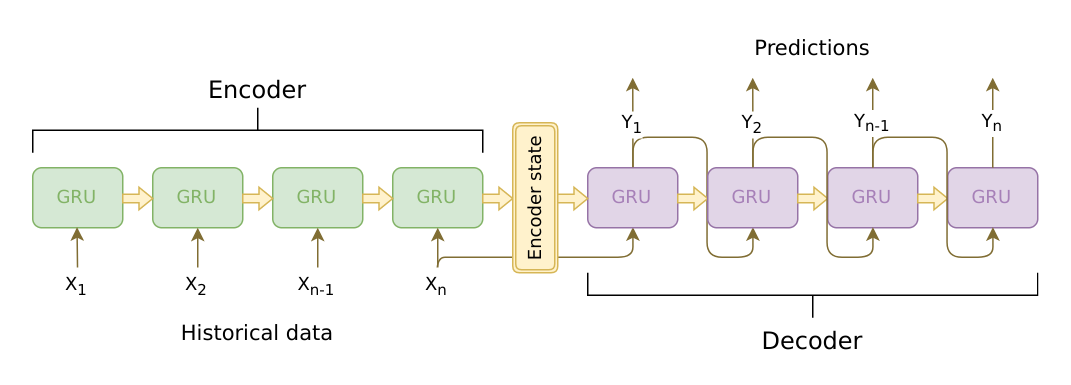
그림 출처: https://jeddy92.github.io/JEddy92.github.io/ts_seq2seq_intro/

인코더

인코더 RNN은 입력 시퀀스를 토큰 단위로(예를 들어, 단어 단위로) 한번에 하나씩 살펴보며 진행합니다. 그리고 각 단계마다 《출력》 벡터와 《은닉 상태》 벡터를 반환합니다. 은닉 상태 벡터는 다음 단계를 진행할 때 같이 사용되며, 출력 벡터는 차례대로 기록됩니다. 인코더는 시퀀스의 각 지점에 대해 파악한 문맥을 고차원 공간에 있는 점들의 집합으로 변환합니다. 나중에 디코더는 이를 이용하여 주어진 문제에 대해 의미 있는 출력을 구할 것입니다.

인코더의 핵심 부분에는 다중 레이어 게이트 순환 유닛(multi-layered Gated Recurrent Unit)이 있습니다. 이는 Cho 등 이 2014년에 고안한 것입니다. 우리는 GRU를 양방향으로 변환한 형태를 사용할 것이며, 이는 본질적으로 두 개의 독립된 RNN이 존재한다는 의미입니다. 하나는 입력 시퀀스를 원래 시퀀스에서의 순서로 처리하며, 다른 하나는 입력 시퀀스를 역순으로 처리합니다. 단계마다 각 네트워크의 출력을 합산합니다. 양방향 GRU를 사용하면 과거와 미래의 문맥을 함께 인코딩할 수 있다는 장점이 있습니다.

양방향 RNN:

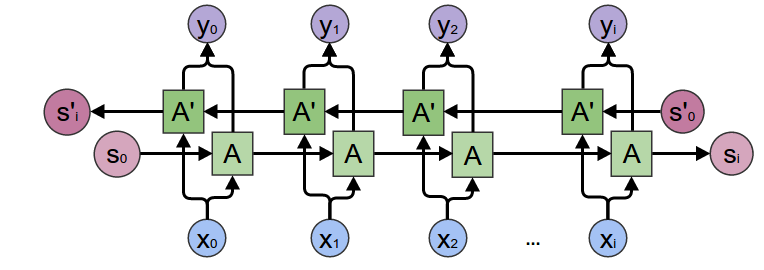
그림 출처: https://colah.github.io/posts/2015-09-NN-Types-FP/

embedding 레이어가 단어 인덱스를 임의 크기의 피처 공간으로 인코딩하는 데 사용되었음에 유의하기 바랍니다. 우리의 모델에서는 이 레이어가 각 단어를 크기가 hidden_size 인 피처 공간으로 매핑할 것입니다. 학습을 거치면 서로 뜻이 유사한 단어는 의미적으로 유사하게 인코딩될 것입니다.

마지막으로, RNN 모듈에 패딩된 배치를 보내려면 RNN과 연결된 부분에서 패킹 및 언패킹하는 작업을 수행해야 합니다. 각각은 nn.utils.rnn.pack_padded_sequence 와 nn.utils.rnn.pad_packed_sequence 를 통해 수행할 수 있습니다.

연산 그래프:

1. 단어 인덱스를 임베딩으로 변환합니다.

2. RNN 모듈을 위한 패딩된 배치 시퀀스를 패킹합니다.

3. GRU로 포워드 패스를 수행합니다.

4. 패딩을 언패킹합니다.

5. 양방향 GRU의 출력을 합산합니다.

6. 출력과 마지막 은닉 상태를 반환합니다.

입력:

• input_seq: 입력 시퀀스 배치. shape=(max_length, batch_size)

• input_lengths: 배치에 포함된 각 문장의 길이로 구성된 리스트. shape=(batch_size)

• hidden: 은닉 상태. shape=(n_layers x num_directions, batch_size, hidden_size)

출력:

• outputs: GRU의 마지막 은닉 레이어에 대한 출력 피처 값(양방향 (출력을 합산한 것). shape=(max_length, batch_size, hidden_size)

• hidden: GRU의 최종 은닉 상태. shape=(n_layers x num_directions, batch_size, hidden_size)

class EncoderRNN(nn.Module):
    def __init__(self, hidden_size, embedding, n_layers=1, dropout=0):
        super(EncoderRNN, self).__init__()
        self.n_layers = n_layers
        self.hidden_size = hidden_size
        self.embedding = embedding

        # GRU를 초기화합니다. input_size와 hidden_size 매개변수는 둘 다 'hidden_size'로
        # 둡니다. 이는 우리 입력의 크기가 hideen_size 만큼의 피처를 갖는 단어 임베딩이기
        # 때문입니다.
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers,
                          dropout=(0 if n_layers == 1 else dropout), bidirectional=True)

    def forward(self, input_seq, input_lengths, hidden=None):
        # 단어 인덱스를 임베딩으로 변환합니다
        embedded = self.embedding(input_seq)
        # RNN 모듈을 위한 패딩된 배치 시퀀스를 패킹합니다
        packed = nn.utils.rnn.pack_padded_sequence(embedded, input_lengths)
        # GRU로 포워드 패스를 수행합니다
        outputs, hidden = self.gru(packed, hidden)
        # 패딩을 언패킹합니다
        outputs, _ = nn.utils.rnn.pad_packed_sequence(outputs)
        # 양방향 GRU의 출력을 합산합니다
        outputs = outputs[:, :, :self.hidden_size] + outputs[:, : ,self.hidden_size:]
        # 출력과 마지막 은닉 상태를 반환합니다
        return outputs, hidden

디코더

디코더 RNN은 토큰 단위로 응답 문장을 생성하는 역할을 수행합니다. 이때 인코더의 문맥 벡터를 사용하며, 내부 은닉 상태에 따라 시퀀스의 다음 단어를 생성하게 됩니다. 디코더는 EOS_token, 즉 문장의 끝을 나타내는 토큰을 출력할 때까지 계속 단어를 생성합니다. 원래의 seq2seq 디코더에는 알려진 문제점이 있습니다. 만약 우리가 입력 시퀀스의 의미를 인코딩할 때 문맥 벡터에만 전적으로 의존한다면, 그 과정 중에 정보 손실이 일어날 가능성이 높다는 것입니다. 이는 특히 입력 시퀀스의 길이가 길 때 그러하며, 이 때문에 디코더의 기능이 크게 제한될 수 있습니다.

이를 해결하기 위한 방편으로, Bahdanau 등 은 〈어텐션 메커니즘’을 고안했습니다. 이는 디코더가 매 단계에 대해 고정된 문맥을 계속 사용하는 것이 아니라, 입력 시퀀스의 특정 부분에 집중하게 하는 방식입니다.

높은 차원에서 이야기 하자면, 어텐션은 디코더의 현재 은닉 상태와 인코더의 출력을 바탕으로 계산됩니다. 출력되는 어텐션 가중치는 입력 시퀀스와 동일한 모양을 가집니다. 따라서 이를 인코더의 출력과 곱할 수 있고, 그 결과로 얻게 되는 가중치 합은 인코더의 출력에서 어느 부분에 집중해야 할지를 알려줍니다. Sean Robertson 의 그림에 이러한 내용이 잘 설명되어 있습니다.

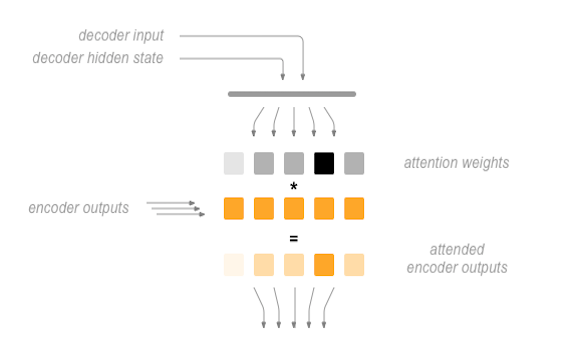
Luong 등 은 Bahdanau의 기초 연구를 더욱 발전시킨 〈전역(global) 어텐션’을 제안했습니다. 〈전역 어텐션’의 핵심적인 차이점은 인코더의 은닉 상태를 모두 고려한다는 점입니다. 이는 Bahdanau 등의 〈지역(local) 어텐션〉 방식이 현재 시점에 대한 인코더의 은닉 상태만을 고려한다는 점과 다른 부분입니다. 〈전역 어텐션’의 또 다른 차이점은 어텐션에 대한 가중치, 혹은 에너지를 계산할 때 현재 시점에 대한 디코더의 은닉 상태만을 사용한다는 점입니다. Bahdanau 등은 어텐션을 계산할 때 디코더의 이전 단계 상태에 대한 정보를 활용합니다. 또한 Luong 등의 방법에서는 인코더의 출력과 디코더의 출력에 대한 어텐션 에너지를 계산하는 방법을 제공하며, 이를 〈점수 함수(score function)〉라 부릅니다.

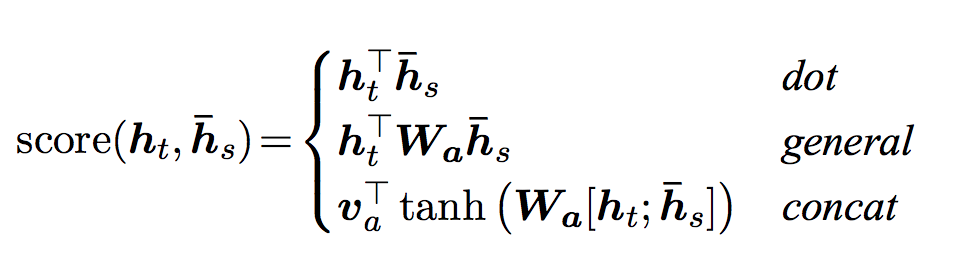
이때 \(h_t\) 는 목표 디코더의 현재 상태를, \(\bar{h}_s\) 는 인코더의 모든 상태를 뜻합니다.

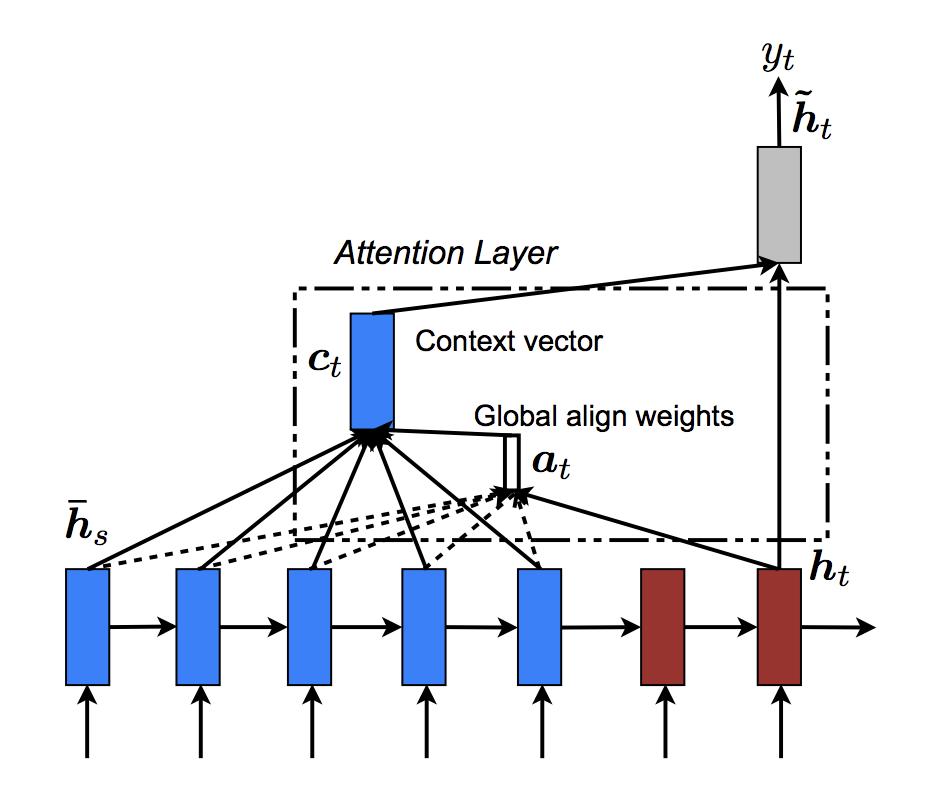
종합해 보면, 전역 어텐션 메커니즘을 다음 그림과 같이 요약할 수 있을 것입니다. 우리가 〈어텐션 레이어’를 Attn 라는 독립적인 nn.Module 로 구현할 것임에 유의하기 바랍니다. 이 모듈의 출력은 모양이 (batch_size, 1, max_length) 인 정규화된 softmax 가중치 텐서입니다.

# Luong 어텐션 레이어
class Attn(nn.Module):
    def __init__(self, method, hidden_size):
        super(Attn, self).__init__()
        self.method = method
        if self.method not in ['dot', 'general', 'concat']:
            raise ValueError(self.method, "is not an appropriate attention method.")
        self.hidden_size = hidden_size
        if self.method == 'general':
            self.attn = nn.Linear(self.hidden_size, hidden_size)
        elif self.method == 'concat':
            self.attn = nn.Linear(self.hidden_size * 2, hidden_size)
            self.v = nn.Parameter(torch.FloatTensor(hidden_size))

    def dot_score(self, hidden, encoder_output):
        return torch.sum(hidden * encoder_output, dim=2)

    def general_score(self, hidden, encoder_output):
        energy = self.attn(encoder_output)
        return torch.sum(hidden * energy, dim=2)

    def concat_score(self, hidden, encoder_output):
        energy = self.attn(torch.cat((hidden.expand(encoder_output.size(0), -1, -1), encoder_output), 2)).tanh()
        return torch.sum(self.v * energy, dim=2)

    def forward(self, hidden, encoder_outputs):
        # Attention 가중치(에너지)를 제안된 방법에 따라 계산합니다
        if self.method == 'general':
            attn_energies = self.general_score(hidden, encoder_outputs)
        elif self.method == 'concat':
            attn_energies = self.concat_score(hidden, encoder_outputs)
        elif self.method == 'dot':
            attn_energies = self.dot_score(hidden, encoder_outputs)

        # max_length와 batch_size의 차원을 뒤집습니다
        attn_energies = attn_energies.t()

        # 정규화된 softmax 확률 점수를 반환합니다 (차원을 늘려서)
        return F.softmax(attn_energies, dim=1).unsqueeze(1)

이처럼 어텐션 서브모듈을 정의하고 나면 실제 디코더 모델을 구현할 수 있게 됩니다. 디코더에 대해서는 매 시간마다 배치를 하나씩 수동으로 제공하려 합니다. 이는 임베딩된 단어 텐서와 GRU 출력의 모양이 둘 다 (1, batch_size, hidden_size) 라는 의미입니다.

연산 그래프:

1. 현재의 입력 단어에 대한 임베딩을 구합니다.

2. 무방향 GRU로 포워드 패스를 수행합니다.

3. (2)에서 구한 현재의 GRU 출력을 바탕으로 어텐션 가중치를 계산합니다.

4. 인코더 출력에 어텐션을 곱하여 새로운 《가중치 합》 문맥 벡터를 구합니다.

5. Luong의 논문에 나온 식 5를 이용하여 가중치 문맥 벡터와 GRU 출력을 결합합니다.

6. Luong의 논문에 나온 식 6을 이용하여(softmax 없이) 다음 단어를 예측합니다.

7. 출력과 마지막 은닉 상태를 반환합니다.

입력:

• input_step: 입력 시퀀스 배치에 대한 한 단위 시간(한 단어). shape=(1, batch_size)

• last_hidden: GRU의 마지막 은닉 레이어. shape=(n_layers x num_directions, batch_size, hidden_size)

• encoder_outputs: 인코더 모델의 출력. shape=(max_length, batch_size, hidden_size)

출력:

• output: 각 단어가 디코딩된 시퀀스에서 다음 단어로 사용되었을 때 적합할 확률을 나타내는 정규화된 softmax 텐서. shape=(batch_size, voc.num_words)

• hidden: GRU의 마지막 은닉 상태. shape=(n_layers x num_directions, batch_size, hidden_size)

class LuongAttnDecoderRNN(nn.Module):
    def __init__(self, attn_model, embedding, hidden_size, output_size, n_layers=1, dropout=0.1):
        super(LuongAttnDecoderRNN, self).__init__()

        # 참조를 보존해 둡니다
        self.attn_model = attn_model
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.n_layers = n_layers
        self.dropout = dropout

        # 레이어를 정의합니다
        self.embedding = embedding
        self.embedding_dropout = nn.Dropout(dropout)
        self.gru = nn.GRU(hidden_size, hidden_size, n_layers, dropout=(0 if n_layers == 1 else dropout))
        self.concat = nn.Linear(hidden_size * 2, hidden_size)
        self.out = nn.Linear(hidden_size, output_size)

        self.attn = Attn(attn_model, hidden_size)

    def forward(self, input_step, last_hidden, encoder_outputs):
        # 주의: 한 단위 시간에 대해 한 단계(단어)만을 수행합니다
        # 현재의 입력 단어에 대한 임베딩을 구합니다
        embedded = self.embedding(input_step)
        embedded = self.embedding_dropout(embedded)
        # 무방향 GRU로 포워드 패스를 수행합니다
        rnn_output, hidden = self.gru(embedded, last_hidden)
        # 현재의 GRU 출력을 바탕으로 어텐션 가중치를 계산합니다
        attn_weights = self.attn(rnn_output, encoder_outputs)
        # 인코더 출력에 어텐션을 곱하여 새로운 "가중치 합" 문맥 벡터를 구합니다
        context = attn_weights.bmm(encoder_outputs.transpose(0, 1))
        # Luong의 논문에 나온 식 5를 이용하여 가중치 문맥 벡터와 GRU 출력을 결합합니다
        rnn_output = rnn_output.squeeze(0)
        context = context.squeeze(1)
        concat_input = torch.cat((rnn_output, context), 1)
        concat_output = torch.tanh(self.concat(concat_input))
        # Luong의 논문에 나온 식 6을 이용하여 다음 단어를 예측합니다
        output = self.out(concat_output)
        output = F.softmax(output, dim=1)
        # 출력과 마지막 은닉 상태를 반환합니다
        return output, hidden

학습 프로시저 정의하기

Masked loss

우리는 패딩된 시퀀스 배치를 다루기 때문에 손실을 계산할 때 단순히 텐서의 모든 원소를 고려할 수는 없습니다. 우리는 maskNLLLoss 를 정의하여 디코더의 출력 텐서, 목표 텐서, 이진 마스크 텐서를 바탕으로 손실을 계산하려 합니다. 이 손실 함수에서는 마스크 텐서의 1 에 대응하는 원소에 대한 음의 로그 우도 값의 평균을 계산합니다.

def maskNLLLoss(inp, target, mask):
    nTotal = mask.sum()
    crossEntropy = -torch.log(torch.gather(inp, 1, target.view(-1, 1)).squeeze(1))
    loss = crossEntropy.masked_select(mask).mean()
    loss = loss.to(device)
    return loss, nTotal.item()

한 번의 학습 단계

train 함수에 학습을 한 단계(입력 배치 한 개에 대한) 진행하는 알고리즘이 나와 있습니다.

우리는 수렴이 잘 되도록 몇 가지 영리한 전략을 사용해보려 합니다.

• 첫 번째 전략은 teacher forcing 을 사용하는 것입니다. 이는 teacher_forcing_ratio 로 정의된 확률에 따라, 디코더의 이번 단계 예측값 대신에 현재의 목표 단어를 디코더의 다음 입력 값으로 활용하는 것입니다. 이 기법은 디코더의 보조 바퀴처럼 작용하여 효율적으로 학습될 수 있게 도와 줍니다. 하지만 teacher forcing 기법은 추론 과정에서 모델이 불안정 해지도록 할 수도 있는데, 이는 디코더가 학습 과정에서 자신의 출력 시퀀스를 직접 만들어 볼 기회를 충분히 제공받지 못할 수 있기 때문입니다. 따라서 우리는 teacher_forcing_ratio 를 어떻게 설정해 두었는지에 주의를 기울여야 하며, 수렴이 빨리 되었다고 속아 넘어가서는 안 됩니다.

• 우리가 구현한 두 번째 전략은 gradient clipping 입니다. 이는 소위 〈그라디언트 폭발〉 문제를 해결하기 위해 널리 사용되는 기법입니다. 핵심은 그라디언트를 클리핑 하거나 임계값을 둠으로써, 그라디언트가 지수 함수적으로 증가하거나 오버플로를 일으키는(NaN) 경우를 막고, 비용 함수의 급격한 경사를 피하겠다는 것입니다.

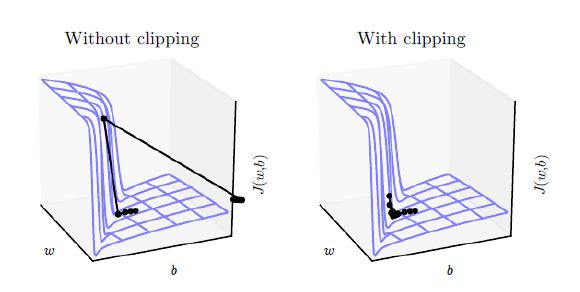
그림 출처: Goodfellow 등 저. Deep Learning. 2016. https://www.deeplearningbook.org/

작업 절차:

1. 전체 입력 배치에 대하여 인코더로 포워드 패스를 수행합니다.

2. 디코더의 입력을 SOS_token로, 은닉 상태를 인코더의 마지막 은닉 상태로 초기화합니다.

3. 입력 배치 시퀀스를 한 번에 하나씩 디코더로 포워드 패스합니다.

4. Teacher forcing을 사용하는 경우, 디코더의 다음 입력을 현재의 목표로 둡니다. 그렇지 않으면 디코더의 다음 입력을 현재 디코더의 출력으로 둡니다.

5. 손실을 계산하고 누적합니다.

6. 역전파를 수행합니다.

7. 그라디언트를 클리핑 합니다.

8. 인코더 및 디코더 모델의 매개변수를 갱신합니다.

경고

PyTorch의 RNN 모듈( RNN, LSTM, GRU )은 전체 입력 시퀀스(또는 시퀀스의 배치)를 단순히 넣어주기만 하면 다른 비순환 레이어처럼 사용할 수 있습니다. 우리는 encoder 에서 GRU 레이어를 이런 식으로 사용합니다. 그 안이 실제로 어떻게 되어 있는지를 살펴보면, 매 시간 단계마다 은닉 상태를 계산하는 반복 프로세스가 존재합니다. 또 다른 방법은, 이 모듈을 매번 한 단위 시간만큼 수행할 수도 있습니다. 그 경우에는 우리가 decoder 모델을 다룰 때처럼, 학습 과정에서 수동으로 시퀀스에 대해 반복 작업을 수행해 주어야 합니다. 이 모듈에 대해 모델의 개념을 확실히 갖고만 있다면, 순차 모델을 구현하는 것도 매우 단순할 것입니다.

def train(input_variable, lengths, target_variable, mask, max_target_len, encoder, decoder, embedding,
          encoder_optimizer, decoder_optimizer, batch_size, clip, max_length=MAX_LENGTH):

    # 제로 그라디언트
    encoder_optimizer.zero_grad()
    decoder_optimizer.zero_grad()

    # device 옵션을 설정합니다
    input_variable = input_variable.to(device)
    target_variable = target_variable.to(device)
    mask = mask.to(device)
    # RNN 패킹의 길이는 항상 CPU에 위치해야 합니다
    lengths = lengths.to("cpu")

    # 변수를 초기화합니다
    loss = 0
    print_losses = []
    n_totals = 0

    # 인코더로 포워드 패스를 수행합니다
    encoder_outputs, encoder_hidden = encoder(input_variable, lengths)

    # 초기 디코더 입력을 생성합니다(각 문장을 SOS 토큰으로 시작합니다)
    decoder_input = torch.LongTensor([[SOS_token for _ in range(batch_size)]])
    decoder_input = decoder_input.to(device)

    # 디코더의 초기 은닉 상태를 인코더의 마지막 은닉 상태로 둡니다
    decoder_hidden = encoder_hidden[:decoder.n_layers]

    # 이번 반복에서 teacher forcing을 사용할지를 결정합니다
    use_teacher_forcing = True if random.random() < teacher_forcing_ratio else False

    # 배치 시퀀스를 한 번에 하나씩 디코더로 포워드 패스합니다
    if use_teacher_forcing:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # Teacher forcing 사용: 다음 입력을 현재의 목표로 둡니다
            decoder_input = target_variable[t].view(1, -1)
            # 손실을 계산하고 누적합니다
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal
    else:
        for t in range(max_target_len):
            decoder_output, decoder_hidden = decoder(
                decoder_input, decoder_hidden, encoder_outputs
            )
            # Teacher forcing 미사용: 다음 입력을 디코더의 출력으로 둡니다
            _, topi = decoder_output.topk(1)
            decoder_input = torch.LongTensor([[topi[i][0] for i in range(batch_size)]])
            decoder_input = decoder_input.to(device)
            # 손실을 계산하고 누적합니다
            mask_loss, nTotal = maskNLLLoss(decoder_output, target_variable[t], mask[t])
            loss += mask_loss
            print_losses.append(mask_loss.item() * nTotal)
            n_totals += nTotal

    # 역전파를 수행합니다
    loss.backward()

    # 그라디언트 클리핑: 그라디언트를 제자리에서 수정합니다
    _ = nn.utils.clip_grad_norm_(encoder.parameters(), clip)
    _ = nn.utils.clip_grad_norm_(decoder.parameters(), clip)

    # 모델의 가중치를 수정합니다
    encoder_optimizer.step()
    decoder_optimizer.step()

    return sum(print_losses) / n_totals

학습 단계

이제 마지막으로 전체 학습 프로시저와 데이터를 하나로 엮을 때가 되었습니다. trainIters 함수는 주어진 모델, optimizer, 데이터 등을 토대로 학습을 n_iterations 번의 단계만큼 진행하는 역할을 담당합니다. 이 함수는 자기 자신을 살 설명하고 있는 편인데, 무거운 작업을 train 함수에 옮겨 놓았기 때문입니다.

한 가지 주의할 점은 우리가 모델을 저장하려 할 때, 인코더와 디코더의 state_dicts (매개변수), optimizer의 state_dicts, 손실, 진행 단계 수 등을 tarball로 만들어 저장한다는 점입니다. 모델을 이러한 방식으로 저장하면 checkpoint에 대해 아주 높은 수준의 유연성을 확보할 수 있게 됩니다. Checkpoint를 불러오고 나면, 우리는 모델 매개변수를 이용하여 예측을 진행할 수도 있고, 이전에 멈췄던 부분부터 학습을 계속 진행할 수도 있게 됩니다.

def trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer, embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size, print_every, save_every, clip, corpus_name, loadFilename):

    # 각 단계에 대한 배치를 읽어옵니다
    training_batches = [batch2TrainData(voc, [random.choice(pairs) for _ in range(batch_size)])
                      for _ in range(n_iteration)]

    # 초기화
    print('Initializing ...')
    start_iteration = 1
    print_loss = 0
    if loadFilename:
        start_iteration = checkpoint['iteration'] + 1

    # 학습 루프
    print("Training...")
    for iteration in range(start_iteration, n_iteration + 1):
        training_batch = training_batches[iteration - 1]
        # 배치에서 각 필드를 읽어옵니다
        input_variable, lengths, target_variable, mask, max_target_len = training_batch

        # 배치에 대해 학습을 한 단계 진행합니다
        loss = train(input_variable, lengths, target_variable, mask, max_target_len, encoder,
                     decoder, embedding, encoder_optimizer, decoder_optimizer, batch_size, clip)
        print_loss += loss

        # 경과를 출력합니다
        if iteration % print_every == 0:
            print_loss_avg = print_loss / print_every
            print("Iteration: {}; Percent complete: {:.1f}%; Average loss: {:.4f}".format(iteration, iteration / n_iteration * 100, print_loss_avg))
            print_loss = 0

        # Checkpoint를 저장합니다
        if (iteration % save_every == 0):
            directory = os.path.join(save_dir, model_name, corpus_name, '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size))
            if not os.path.exists(directory):
                os.makedirs(directory)
            torch.save({
                'iteration': iteration,
                'en': encoder.state_dict(),
                'de': decoder.state_dict(),
                'en_opt': encoder_optimizer.state_dict(),
                'de_opt': decoder_optimizer.state_dict(),
                'loss': loss,
                'voc_dict': voc.__dict__,
                'embedding': embedding.state_dict()
            }, os.path.join(directory, '{}_{}.tar'.format(iteration, 'checkpoint')))

평가 정의하기

모델을 학습시키고 나면 직접 봇과 대화를 나눠보고 싶어질 것입니다. 그러려면 먼저 모델이 인코딩된 입력을 어떻게 디코딩할지를 정의해줘야 합니다.

탐욕적 디코딩

탐욕적 디코딩(Greedy decoding)은 우리가 학습 단계에서 teacher forcing을 적용하지 않았을 때 사용한 디코딩 방법입니다. 달리 말하면, 각 단계에 대해 단순히 decoder_output 에서 가장 높은 softmax값을 갖는 단어를 선택하는 방식입니다. 이 디코딩 방법은 한 번의 단계에 대해서는 최적입니다.

우리는 탐욕적 디코딩 연산을 수행할 수 있도록 GreedySearchDecoder 클래스를 만들었습니다. 수행 과정에서 이 클래스의 인스턴스는 모양이 (input_seq length, 1) 인 입력 시퀀스( input_seq ), 조종할 입력 길이( input_length ) 텐서, 그리고 응답 문장 길이의 제한을 나타내는 max_length 를 입력으로 받습니다. 입력 시퀀서는 다음과 같은 계산 그래프에 의해 평가됩니다.

연산 그래프:

1. 인코더 모델로 입력을 포워드 패스합니다.

2. 인코더의 마지막 은닉 레이어가 디코더의 첫 번째 은닉 레이어의 입력이 되도록 준비합니다.

3. 디코더의 첫 번째 입력을 SOS_token으로 초기화합니다.

4. 디코더가 단어를 덧붙여 나갈 텐서를 초기화합니다.

5. 반복적으로 각 단계마다 하나의 단어 토큰을 디코딩합니다.

   1. 디코더로의 포워드 패스를 수행합니다.

   2. 가장 가능성 높은 단어 토큰과 그 softmax 점수를 구합니다.

   3. 토큰과 점수를 기록합니다.

   4. 현재의 토큰을 디코더의 다음 입력으로 준비시킵니다.

6. 단어 토큰과 점수를 모아서 반환합니다.

class GreedySearchDecoder(nn.Module):
    def __init__(self, encoder, decoder):
        super(GreedySearchDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder

    def forward(self, input_seq, input_length, max_length):
        # 인코더 모델로 입력을 포워드 패스합니다
        encoder_outputs, encoder_hidden = self.encoder(input_seq, input_length)
        # 인코더의 마지막 은닉 레이어가 디코더의 첫 번째 은닉 레이어의 입력이 되도록 준비합니다
        decoder_hidden = encoder_hidden[:decoder.n_layers]
        # 디코더의 첫 번째 입력을 SOS_token으로 초기화합니다
        decoder_input = torch.ones(1, 1, device=device, dtype=torch.long) * SOS_token
        # 디코더가 단어를 덧붙여 나갈 텐서를 초기화합니다
        all_tokens = torch.zeros([0], device=device, dtype=torch.long)
        all_scores = torch.zeros([0], device=device)
        # 반복적으로 각 단계마다 하나의 단어 토큰을 디코딩합니다
        for _ in range(max_length):
            # 디코더로의 포워드 패스를 수행합니다
            decoder_output, decoder_hidden = self.decoder(decoder_input, decoder_hidden, encoder_outputs)
            # 가장 가능성 높은 단어 토큰과 그 softmax 점수를 구합니다
            decoder_scores, decoder_input = torch.max(decoder_output, dim=1)
            # 토큰과 점수를 기록합니다
            all_tokens = torch.cat((all_tokens, decoder_input), dim=0)
            all_scores = torch.cat((all_scores, decoder_scores), dim=0)
            # 현재의 토큰을 디코더의 다음 입력으로 준비시킵니다(차원을 증가시켜서)
            decoder_input = torch.unsqueeze(decoder_input, 0)
        # 단어 토큰과 점수를 모아서 반환합니다
        return all_tokens, all_scores

내 텍스트 평가하기

이제 디코딩 모델을 정의했으니, 문자열로 된 입력 시퀀스를 평가하는 함수를 작성해볼 수 있을 것입니다. evaluate 함수에 입력 시퀀스를 낮은 레벨에서 어떻게 처리할지가 나와 있습니다. 우리는 먼저 문장을 batch_size==1 이고 단어 인덱스로 구성된 입력 배치 형태로 만듭니다. 이를 위해 문장의 각 단어를 그에 대응하는 인덱스로 변환하고, 차원을 뒤집어서 모델에 맞는 입력 형태로 변환합니다. 우리는 입력 시퀀스의 길이를 저장하고 있는 lengths 텐서도 만듭니다. 이 경우에는 lengths 가 스칼라 값이 되는데, 우리는 한 번에 한 문장만 평가하기 때문입니다(batch_size==1). 다음으로는 GreedySearchDecoder 의 객체(searcher)를 이용하여 응답 문장 텐서를 디코딩합니다. 마지막으로, 응답 인덱스를 단어로 변환하고 디코딩된 단어의 리스트를 반환합니다.

evaluateInput 은 우리의 챗봇에 대한 인터페이스 역할을 수행합니다. 이를 호출하면 입력 텍스트 필드가 생성되는데, 거기에 우리의 질의 문장을 입력해볼 수 있습니다. 입력 문장을 타이핑하고 엔터 를 누르면, 입력한 텍스트가 학습 데이터와 같은 방식으로 정규화되고, 최종적으로는 evaluate 함수에 입력으로 제공되어 디코딩된 출력 문장을 구하게 됩니다. 우리는 이러한 과정을 계속 반복하며, 이를 통해 〈q’나 〈quit’를 입력하기 전까지는 계속 채팅할 수 있습니다.

마지막으로, 만약 어휘집에 포함되어 있지 않은 단어를 포함하고 있는 문장이 입력되더라도 이를 예의 바르게 처리합니다. 즉 에러 메시지를 출력하고 사용자에게 새로운 문장을 입력해달라고 요청합니다.

def evaluate(encoder, decoder, searcher, voc, sentence, max_length=MAX_LENGTH):
    ### 입력 시퀀스를 배치 형태로 만듭니다
    # 단어 -> 인덱스
    indexes_batch = [indexesFromSentence(voc, sentence)]
    # lengths 텐서를 만듭니다
    lengths = torch.tensor([len(indexes) for indexes in indexes_batch])
    # 배치의 차원을 뒤집어서 모델이 사용하는 형태로 만듭니다
    input_batch = torch.LongTensor(indexes_batch).transpose(0, 1)
    # 적절한 디바이스를 사용합니다
    input_batch = input_batch.to(device)
    lengths = lengths.to("cpu")
    # searcher를 이용하여 문장을 디코딩합니다
    tokens, scores = searcher(input_batch, lengths, max_length)
    # 인덱스 -> 단어
    decoded_words = [voc.index2word[token.item()] for token in tokens]
    return decoded_words


def evaluateInput(encoder, decoder, searcher, voc):
    input_sentence = ''
    while(1):
        try:
            # 입력 문장을 받아옵니다
            input_sentence = input('> ')
            # 종료 조건인지 검사합니다
            if input_sentence == 'q' or input_sentence == 'quit': break
            # 문장을 정규화합니다
            input_sentence = normalizeString(input_sentence)
            # 문장을 평가합니다
            output_words = evaluate(encoder, decoder, searcher, voc, input_sentence)
            # 응답 문장을 형식에 맞춰 출력합니다
            output_words[:] = [x for x in output_words if not (x == 'EOS' or x == 'PAD')]
            print('Bot:', ' '.join(output_words))

        except KeyError:
            print("Error: Encountered unknown word.")

모델 수행하기

마지막으로, 우리의 모델을 수행해 볼 시간입니다!

우리가 챗봇 모델을 학습할 때든 테스트할 때든, 우리는 각각의 인코더 및 디코더 모델을 초기화해줘야 합니다. 다음 블록에서는 우리가 원하는대로 설정을 맞추고, 처음부터 시작할지, 아니면 checkpoint를 불러올지 정하고, 모델을 빌드하고 초기화합니다. 성능을 최적화하기 위해서는 모델 설정을 여러가지로 바꿔 보면서 테스트해보기 바랍니다.

# 모델을 설정합니다
model_name = 'cb_model'
attn_model = 'dot'
#``attn_model = 'general'``
#``attn_model = 'concat'``
hidden_size = 500
encoder_n_layers = 2
decoder_n_layers = 2
dropout = 0.1
batch_size = 64

# 불러올 checkpoint를 설정합니다. 처음부터 시작할 때는 None으로 둡니다.
loadFilename = None
checkpoint_iter = 4000

checkpoint로부터 불러오는 샘플 코드:

loadFilename = os.path.join(save_dir, model_name, corpus_name,
                    '{}-{}_{}'.format(encoder_n_layers, decoder_n_layers, hidden_size),
                    '{}_checkpoint.tar'.format(checkpoint_iter))

# ``loadFilename`` 이 존재하는 경우에는 모델을 불러옵니다
if loadFilename:
    # 모델을 학습할 때와 같은 기기에서 불러오는 경우
    checkpoint = torch.load(loadFilename)
    # GPU에서 학습한 모델을 CPU로 불러오는 경우
    #checkpoint = torch.load(loadFilename, map_location=torch.device('cpu'))
    encoder_sd = checkpoint['en']
    decoder_sd = checkpoint['de']
    encoder_optimizer_sd = checkpoint['en_opt']
    decoder_optimizer_sd = checkpoint['de_opt']
    embedding_sd = checkpoint['embedding']
    voc.__dict__ = checkpoint['voc_dict']


print('Building encoder and decoder ...')
# 단어 임베딩을 초기화합니다
embedding = nn.Embedding(voc.num_words, hidden_size)
if loadFilename:
    embedding.load_state_dict(embedding_sd)
# 인코더 및 디코더 모델을 초기화합니다
encoder = EncoderRNN(hidden_size, embedding, encoder_n_layers, dropout)
decoder = LuongAttnDecoderRNN(attn_model, embedding, hidden_size, voc.num_words, decoder_n_layers, dropout)
if loadFilename:
    encoder.load_state_dict(encoder_sd)
    decoder.load_state_dict(decoder_sd)
# 적절한 디바이스를 사용합니다
encoder = encoder.to(device)
decoder = decoder.to(device)
print('Models built and ready to go!')

Building encoder and decoder ...
Models built and ready to go!

학습 수행하기

모델을 학습해보고 싶다면 다음 블록을 수행하면 됩니다.

먼저 학습 매개변수를 설정하고, optimizer를 초기화한 뒤, 마지막으로 trainIters 함수를 호출하여 학습 단계를 진행합니다.

# 학습 및 최적화 설정
clip = 50.0
teacher_forcing_ratio = 1.0
learning_rate = 0.0001
decoder_learning_ratio = 5.0
n_iteration = 4000
print_every = 1
save_every = 500

# Dropout 레이어를 학습 모드로 둡니다
encoder.train()
decoder.train()

# Optimizer를 초기화합니다
print('Building optimizers ...')
encoder_optimizer = optim.Adam(encoder.parameters(), lr=learning_rate)
decoder_optimizer = optim.Adam(decoder.parameters(), lr=learning_rate * decoder_learning_ratio)
if loadFilename:
    encoder_optimizer.load_state_dict(encoder_optimizer_sd)
    decoder_optimizer.load_state_dict(decoder_optimizer_sd)

# CUDA가 있으면 CUDA를 설정합니다
for state in encoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.cuda()

for state in decoder_optimizer.state.values():
    for k, v in state.items():
        if isinstance(v, torch.Tensor):
            state[k] = v.cuda()

# 학습 단계를 수행합니다
print("Starting Training!")
trainIters(model_name, voc, pairs, encoder, decoder, encoder_optimizer, decoder_optimizer,
           embedding, encoder_n_layers, decoder_n_layers, save_dir, n_iteration, batch_size,
           print_every, save_every, clip, corpus_name, loadFilename)

Building optimizers ...
Starting Training!
Initializing ...
Training...
Iteration: 1; Percent complete: 0.0%; Average loss: 8.9564
Iteration: 2; Percent complete: 0.1%; Average loss: 8.8302
Iteration: 3; Percent complete: 0.1%; Average loss: 8.5976
Iteration: 4; Percent complete: 0.1%; Average loss: 8.2953
Iteration: 5; Percent complete: 0.1%; Average loss: 7.9397
Iteration: 6; Percent complete: 0.1%; Average loss: 7.3357
Iteration: 7; Percent complete: 0.2%; Average loss: 6.8529
Iteration: 8; Percent complete: 0.2%; Average loss: 6.8305
Iteration: 9; Percent complete: 0.2%; Average loss: 6.9018
Iteration: 10; Percent complete: 0.2%; Average loss: 6.5908
Iteration: 11; Percent complete: 0.3%; Average loss: 6.1848
Iteration: 12; Percent complete: 0.3%; Average loss: 5.9733
Iteration: 13; Percent complete: 0.3%; Average loss: 5.7504
Iteration: 14; Percent complete: 0.4%; Average loss: 5.6561
Iteration: 15; Percent complete: 0.4%; Average loss: 5.6535
Iteration: 16; Percent complete: 0.4%; Average loss: 5.5807
Iteration: 17; Percent complete: 0.4%; Average loss: 5.2246
Iteration: 18; Percent complete: 0.4%; Average loss: 5.1463
Iteration: 19; Percent complete: 0.5%; Average loss: 5.1951
Iteration: 20; Percent complete: 0.5%; Average loss: 4.7788
Iteration: 21; Percent complete: 0.5%; Average loss: 5.1142
Iteration: 22; Percent complete: 0.5%; Average loss: 4.8746
Iteration: 23; Percent complete: 0.6%; Average loss: 5.1111
Iteration: 24; Percent complete: 0.6%; Average loss: 4.9173
Iteration: 25; Percent complete: 0.6%; Average loss: 5.0223
Iteration: 26; Percent complete: 0.7%; Average loss: 4.7115
Iteration: 27; Percent complete: 0.7%; Average loss: 4.8900
Iteration: 28; Percent complete: 0.7%; Average loss: 4.8807
Iteration: 29; Percent complete: 0.7%; Average loss: 4.7677
Iteration: 30; Percent complete: 0.8%; Average loss: 4.9645
Iteration: 31; Percent complete: 0.8%; Average loss: 4.6627
Iteration: 32; Percent complete: 0.8%; Average loss: 4.8106
Iteration: 33; Percent complete: 0.8%; Average loss: 4.7339
Iteration: 34; Percent complete: 0.9%; Average loss: 4.7549
Iteration: 35; Percent complete: 0.9%; Average loss: 4.7848
Iteration: 36; Percent complete: 0.9%; Average loss: 4.8098
Iteration: 37; Percent complete: 0.9%; Average loss: 4.8194
Iteration: 38; Percent complete: 0.9%; Average loss: 4.7376
Iteration: 39; Percent complete: 1.0%; Average loss: 5.0262
Iteration: 40; Percent complete: 1.0%; Average loss: 4.7121
Iteration: 41; Percent complete: 1.0%; Average loss: 4.6511
Iteration: 42; Percent complete: 1.1%; Average loss: 4.8947
Iteration: 43; Percent complete: 1.1%; Average loss: 4.7295
Iteration: 44; Percent complete: 1.1%; Average loss: 4.7662
Iteration: 45; Percent complete: 1.1%; Average loss: 4.7463
Iteration: 46; Percent complete: 1.1%; Average loss: 4.7885
Iteration: 47; Percent complete: 1.2%; Average loss: 4.7841
Iteration: 48; Percent complete: 1.2%; Average loss: 4.5277
Iteration: 49; Percent complete: 1.2%; Average loss: 4.4461
Iteration: 50; Percent complete: 1.2%; Average loss: 4.6152
Iteration: 51; Percent complete: 1.3%; Average loss: 4.6765
Iteration: 52; Percent complete: 1.3%; Average loss: 4.7606
Iteration: 53; Percent complete: 1.3%; Average loss: 4.6306
Iteration: 54; Percent complete: 1.4%; Average loss: 4.8312
Iteration: 55; Percent complete: 1.4%; Average loss: 4.7298
Iteration: 56; Percent complete: 1.4%; Average loss: 4.5886
Iteration: 57; Percent complete: 1.4%; Average loss: 4.6449
Iteration: 58; Percent complete: 1.5%; Average loss: 4.5457
Iteration: 59; Percent complete: 1.5%; Average loss: 4.8818
Iteration: 60; Percent complete: 1.5%; Average loss: 4.5919
Iteration: 61; Percent complete: 1.5%; Average loss: 4.5860
Iteration: 62; Percent complete: 1.6%; Average loss: 4.5730
Iteration: 63; Percent complete: 1.6%; Average loss: 4.6844
Iteration: 64; Percent complete: 1.6%; Average loss: 4.5951
Iteration: 65; Percent complete: 1.6%; Average loss: 4.4716
Iteration: 66; Percent complete: 1.7%; Average loss: 4.7183
Iteration: 67; Percent complete: 1.7%; Average loss: 4.4383
Iteration: 68; Percent complete: 1.7%; Average loss: 4.3772
Iteration: 69; Percent complete: 1.7%; Average loss: 4.6802
Iteration: 70; Percent complete: 1.8%; Average loss: 4.5356
Iteration: 71; Percent complete: 1.8%; Average loss: 4.4845
Iteration: 72; Percent complete: 1.8%; Average loss: 4.5824
Iteration: 73; Percent complete: 1.8%; Average loss: 4.5345
Iteration: 74; Percent complete: 1.8%; Average loss: 4.3615
Iteration: 75; Percent complete: 1.9%; Average loss: 4.5651
Iteration: 76; Percent complete: 1.9%; Average loss: 4.3655
Iteration: 77; Percent complete: 1.9%; Average loss: 4.6131
Iteration: 78; Percent complete: 1.9%; Average loss: 4.3827
Iteration: 79; Percent complete: 2.0%; Average loss: 4.6266
Iteration: 80; Percent complete: 2.0%; Average loss: 4.6155
Iteration: 81; Percent complete: 2.0%; Average loss: 4.3596
Iteration: 82; Percent complete: 2.1%; Average loss: 4.3404
Iteration: 83; Percent complete: 2.1%; Average loss: 4.5251
Iteration: 84; Percent complete: 2.1%; Average loss: 4.6516
Iteration: 85; Percent complete: 2.1%; Average loss: 4.4820
Iteration: 86; Percent complete: 2.1%; Average loss: 4.7006
Iteration: 87; Percent complete: 2.2%; Average loss: 4.0852
Iteration: 88; Percent complete: 2.2%; Average loss: 4.2784
Iteration: 89; Percent complete: 2.2%; Average loss: 4.4359
Iteration: 90; Percent complete: 2.2%; Average loss: 4.5605
Iteration: 91; Percent complete: 2.3%; Average loss: 4.3669
Iteration: 92; Percent complete: 2.3%; Average loss: 4.4328
Iteration: 93; Percent complete: 2.3%; Average loss: 4.1790
Iteration: 94; Percent complete: 2.4%; Average loss: 4.4985
Iteration: 95; Percent complete: 2.4%; Average loss: 4.3336
Iteration: 96; Percent complete: 2.4%; Average loss: 4.5487
Iteration: 97; Percent complete: 2.4%; Average loss: 4.3713
Iteration: 98; Percent complete: 2.5%; Average loss: 4.4859
Iteration: 99; Percent complete: 2.5%; Average loss: 4.4648
Iteration: 100; Percent complete: 2.5%; Average loss: 4.3953
Iteration: 101; Percent complete: 2.5%; Average loss: 4.1291
Iteration: 102; Percent complete: 2.5%; Average loss: 4.1750
Iteration: 103; Percent complete: 2.6%; Average loss: 4.4464
Iteration: 104; Percent complete: 2.6%; Average loss: 4.6059
Iteration: 105; Percent complete: 2.6%; Average loss: 4.4745
Iteration: 106; Percent complete: 2.6%; Average loss: 4.4822
Iteration: 107; Percent complete: 2.7%; Average loss: 4.3695
Iteration: 108; Percent complete: 2.7%; Average loss: 4.5268
Iteration: 109; Percent complete: 2.7%; Average loss: 4.4095
Iteration: 110; Percent complete: 2.8%; Average loss: 4.1611
Iteration: 111; Percent complete: 2.8%; Average loss: 4.3156
Iteration: 112; Percent complete: 2.8%; Average loss: 4.4440
Iteration: 113; Percent complete: 2.8%; Average loss: 4.2477
Iteration: 114; Percent complete: 2.9%; Average loss: 4.4679
Iteration: 115; Percent complete: 2.9%; Average loss: 4.2940
Iteration: 116; Percent complete: 2.9%; Average loss: 4.3510
Iteration: 117; Percent complete: 2.9%; Average loss: 4.4066
Iteration: 118; Percent complete: 2.9%; Average loss: 4.5248
Iteration: 119; Percent complete: 3.0%; Average loss: 4.0505
Iteration: 120; Percent complete: 3.0%; Average loss: 4.0584
Iteration: 121; Percent complete: 3.0%; Average loss: 4.2435
Iteration: 122; Percent complete: 3.0%; Average loss: 4.2925
Iteration: 123; Percent complete: 3.1%; Average loss: 4.3617
Iteration: 124; Percent complete: 3.1%; Average loss: 4.5769
Iteration: 125; Percent complete: 3.1%; Average loss: 4.3301
Iteration: 126; Percent complete: 3.1%; Average loss: 4.3836
Iteration: 127; Percent complete: 3.2%; Average loss: 4.4775
Iteration: 128; Percent complete: 3.2%; Average loss: 4.4591
Iteration: 129; Percent complete: 3.2%; Average loss: 4.3053
Iteration: 130; Percent complete: 3.2%; Average loss: 4.1538
Iteration: 131; Percent complete: 3.3%; Average loss: 4.1197
Iteration: 132; Percent complete: 3.3%; Average loss: 4.4977
Iteration: 133; Percent complete: 3.3%; Average loss: 4.2997
Iteration: 134; Percent complete: 3.4%; Average loss: 4.5115
Iteration: 135; Percent complete: 3.4%; Average loss: 4.2035
Iteration: 136; Percent complete: 3.4%; Average loss: 4.2744
Iteration: 137; Percent complete: 3.4%; Average loss: 4.4225
Iteration: 138; Percent complete: 3.5%; Average loss: 4.3541
Iteration: 139; Percent complete: 3.5%; Average loss: 4.1347
Iteration: 140; Percent complete: 3.5%; Average loss: 3.8422
Iteration: 141; Percent complete: 3.5%; Average loss: 4.2117
Iteration: 142; Percent complete: 3.5%; Average loss: 4.0667
Iteration: 143; Percent complete: 3.6%; Average loss: 4.3994
Iteration: 144; Percent complete: 3.6%; Average loss: 4.3019
Iteration: 145; Percent complete: 3.6%; Average loss: 4.1120
Iteration: 146; Percent complete: 3.6%; Average loss: 4.1506
Iteration: 147; Percent complete: 3.7%; Average loss: 4.1617
Iteration: 148; Percent complete: 3.7%; Average loss: 4.2694
Iteration: 149; Percent complete: 3.7%; Average loss: 4.1855
Iteration: 150; Percent complete: 3.8%; Average loss: 4.1792
Iteration: 151; Percent complete: 3.8%; Average loss: 4.2040
Iteration: 152; Percent complete: 3.8%; Average loss: 4.1385
Iteration: 153; Percent complete: 3.8%; Average loss: 4.1479
Iteration: 154; Percent complete: 3.9%; Average loss: 4.2767
Iteration: 155; Percent complete: 3.9%; Average loss: 4.2087
Iteration: 156; Percent complete: 3.9%; Average loss: 4.4093
Iteration: 157; Percent complete: 3.9%; Average loss: 3.9879
Iteration: 158; Percent complete: 4.0%; Average loss: 4.1966
Iteration: 159; Percent complete: 4.0%; Average loss: 4.1869
Iteration: 160; Percent complete: 4.0%; Average loss: 4.0616
Iteration: 161; Percent complete: 4.0%; Average loss: 4.4225
Iteration: 162; Percent complete: 4.0%; Average loss: 4.4198
Iteration: 163; Percent complete: 4.1%; Average loss: 4.3589
Iteration: 164; Percent complete: 4.1%; Average loss: 4.3919
Iteration: 165; Percent complete: 4.1%; Average loss: 4.0564
Iteration: 166; Percent complete: 4.2%; Average loss: 4.2726
Iteration: 167; Percent complete: 4.2%; Average loss: 4.4428
Iteration: 168; Percent complete: 4.2%; Average loss: 4.1909
Iteration: 169; Percent complete: 4.2%; Average loss: 4.2662
Iteration: 170; Percent complete: 4.2%; Average loss: 4.0663
Iteration: 171; Percent complete: 4.3%; Average loss: 4.2529
Iteration: 172; Percent complete: 4.3%; Average loss: 4.1874
Iteration: 173; Percent complete: 4.3%; Average loss: 4.1244
Iteration: 174; Percent complete: 4.3%; Average loss: 4.4376
Iteration: 175; Percent complete: 4.4%; Average loss: 4.1032
Iteration: 176; Percent complete: 4.4%; Average loss: 4.1790
Iteration: 177; Percent complete: 4.4%; Average loss: 4.6328
Iteration: 178; Percent complete: 4.5%; Average loss: 4.0809
Iteration: 179; Percent complete: 4.5%; Average loss: 4.1995
Iteration: 180; Percent complete: 4.5%; Average loss: 4.1423
Iteration: 181; Percent complete: 4.5%; Average loss: 4.1171
Iteration: 182; Percent complete: 4.5%; Average loss: 4.1619
Iteration: 183; Percent complete: 4.6%; Average loss: 4.1512
Iteration: 184; Percent complete: 4.6%; Average loss: 4.2802
Iteration: 185; Percent complete: 4.6%; Average loss: 4.1611
Iteration: 186; Percent complete: 4.7%; Average loss: 3.9434
Iteration: 187; Percent complete: 4.7%; Average loss: 4.2139
Iteration: 188; Percent complete: 4.7%; Average loss: 4.2643
Iteration: 189; Percent complete: 4.7%; Average loss: 4.2208
Iteration: 190; Percent complete: 4.8%; Average loss: 3.9401
Iteration: 191; Percent complete: 4.8%; Average loss: 4.1063
Iteration: 192; Percent complete: 4.8%; Average loss: 4.1287
Iteration: 193; Percent complete: 4.8%; Average loss: 4.0617
Iteration: 194; Percent complete: 4.9%; Average loss: 4.2164
Iteration: 195; Percent complete: 4.9%; Average loss: 4.1523
Iteration: 196; Percent complete: 4.9%; Average loss: 4.1301
Iteration: 197; Percent complete: 4.9%; Average loss: 4.2990
Iteration: 198; Percent complete: 5.0%; Average loss: 3.9091
Iteration: 199; Percent complete: 5.0%; Average loss: 4.1118
Iteration: 200; Percent complete: 5.0%; Average loss: 4.1807
Iteration: 201; Percent complete: 5.0%; Average loss: 4.2803
Iteration: 202; Percent complete: 5.1%; Average loss: 4.2258
Iteration: 203; Percent complete: 5.1%; Average loss: 4.1471
Iteration: 204; Percent complete: 5.1%; Average loss: 3.9976
Iteration: 205; Percent complete: 5.1%; Average loss: 4.2835
Iteration: 206; Percent complete: 5.1%; Average loss: 3.9930
Iteration: 207; Percent complete: 5.2%; Average loss: 4.2601
Iteration: 208; Percent complete: 5.2%; Average loss: 3.8243
Iteration: 209; Percent complete: 5.2%; Average loss: 3.8666
Iteration: 210; Percent complete: 5.2%; Average loss: 4.2588
Iteration: 211; Percent complete: 5.3%; Average loss: 4.1575
Iteration: 212; Percent complete: 5.3%; Average loss: 4.1044
Iteration: 213; Percent complete: 5.3%; Average loss: 4.1236
Iteration: 214; Percent complete: 5.3%; Average loss: 4.3268
Iteration: 215; Percent complete: 5.4%; Average loss: 4.1986
Iteration: 216; Percent complete: 5.4%; Average loss: 4.2655
Iteration: 217; Percent complete: 5.4%; Average loss: 4.1831
Iteration: 218; Percent complete: 5.5%; Average loss: 4.0121
Iteration: 219; Percent complete: 5.5%; Average loss: 4.0646
Iteration: 220; Percent complete: 5.5%; Average loss: 4.0901
Iteration: 221; Percent complete: 5.5%; Average loss: 3.9481
Iteration: 222; Percent complete: 5.5%; Average loss: 4.2894
Iteration: 223; Percent complete: 5.6%; Average loss: 4.1124
Iteration: 224; Percent complete: 5.6%; Average loss: 4.0288
Iteration: 225; Percent complete: 5.6%; Average loss: 4.0014
Iteration: 226; Percent complete: 5.7%; Average loss: 4.2027
Iteration: 227; Percent complete: 5.7%; Average loss: 3.7143
Iteration: 228; Percent complete: 5.7%; Average loss: 4.2179
Iteration: 229; Percent complete: 5.7%; Average loss: 3.9523
Iteration: 230; Percent complete: 5.8%; Average loss: 4.3313
Iteration: 231; Percent complete: 5.8%; Average loss: 3.8357
Iteration: 232; Percent complete: 5.8%; Average loss: 4.0296
Iteration: 233; Percent complete: 5.8%; Average loss: 3.6873
Iteration: 234; Percent complete: 5.9%; Average loss: 3.7310
Iteration: 235; Percent complete: 5.9%; Average loss: 3.8752
Iteration: 236; Percent complete: 5.9%; Average loss: 4.1744
Iteration: 237; Percent complete: 5.9%; Average loss: 4.1027
Iteration: 238; Percent complete: 5.9%; Average loss: 3.6516
Iteration: 239; Percent complete: 6.0%; Average loss: 3.4337
Iteration: 240; Percent complete: 6.0%; Average loss: 3.7999
Iteration: 241; Percent complete: 6.0%; Average loss: 4.1564
Iteration: 242; Percent complete: 6.0%; Average loss: 4.0872
Iteration: 243; Percent complete: 6.1%; Average loss: 4.2474
Iteration: 244; Percent complete: 6.1%; Average loss: 4.0403
Iteration: 245; Percent complete: 6.1%; Average loss: 4.1199
Iteration: 246; Percent complete: 6.2%; Average loss: 4.0232
Iteration: 247; Percent complete: 6.2%; Average loss: 3.8811
Iteration: 248; Percent complete: 6.2%; Average loss: 4.1007
Iteration: 249; Percent complete: 6.2%; Average loss: 4.1037
Iteration: 250; Percent complete: 6.2%; Average loss: 4.1256
Iteration: 251; Percent complete: 6.3%; Average loss: 3.8127
Iteration: 252; Percent complete: 6.3%; Average loss: 3.8635
Iteration: 253; Percent complete: 6.3%; Average loss: 4.0640
Iteration: 254; Percent complete: 6.3%; Average loss: 3.8229
Iteration: 255; Percent complete: 6.4%; Average loss: 3.9093
Iteration: 256; Percent complete: 6.4%; Average loss: 3.9696
Iteration: 257; Percent complete: 6.4%; Average loss: 4.0974
Iteration: 258; Percent complete: 6.5%; Average loss: 4.0386
Iteration: 259; Percent complete: 6.5%; Average loss: 3.8220
Iteration: 260; Percent complete: 6.5%; Average loss: 4.0868
Iteration: 261; Percent complete: 6.5%; Average loss: 3.6992
Iteration: 262; Percent complete: 6.6%; Average loss: 4.2816
Iteration: 263; Percent complete: 6.6%; Average loss: 4.0134
Iteration: 264; Percent complete: 6.6%; Average loss: 4.1682
Iteration: 265; Percent complete: 6.6%; Average loss: 3.9939
Iteration: 266; Percent complete: 6.7%; Average loss: 4.1088
Iteration: 267; Percent complete: 6.7%; Average loss: 4.0146
Iteration: 268; Percent complete: 6.7%; Average loss: 3.9794
Iteration: 269; Percent complete: 6.7%; Average loss: 4.1150
Iteration: 270; Percent complete: 6.8%; Average loss: 3.8239
Iteration: 271; Percent complete: 6.8%; Average loss: 3.9691
Iteration: 272; Percent complete: 6.8%; Average loss: 4.0533
Iteration: 273; Percent complete: 6.8%; Average loss: 4.2451
Iteration: 274; Percent complete: 6.9%; Average loss: 4.0952
Iteration: 275; Percent complete: 6.9%; Average loss: 3.9836
Iteration: 276; Percent complete: 6.9%; Average loss: 4.0076
Iteration: 277; Percent complete: 6.9%; Average loss: 4.0026
Iteration: 278; Percent complete: 7.0%; Average loss: 3.8051
Iteration: 279; Percent complete: 7.0%; Average loss: 3.8672
Iteration: 280; Percent complete: 7.0%; Average loss: 3.8473
Iteration: 281; Percent complete: 7.0%; Average loss: 3.8596
Iteration: 282; Percent complete: 7.0%; Average loss: 3.8767
Iteration: 283; Percent complete: 7.1%; Average loss: 3.9823
Iteration: 284; Percent complete: 7.1%; Average loss: 3.8252
Iteration: 285; Percent complete: 7.1%; Average loss: 4.1851
Iteration: 286; Percent complete: 7.1%; Average loss: 3.8707
Iteration: 287; Percent complete: 7.2%; Average loss: 4.2260
Iteration: 288; Percent complete: 7.2%; Average loss: 3.9071
Iteration: 289; Percent complete: 7.2%; Average loss: 3.6871
Iteration: 290; Percent complete: 7.2%; Average loss: 3.6541
Iteration: 291; Percent complete: 7.3%; Average loss: 3.6760
Iteration: 292; Percent complete: 7.3%; Average loss: 3.9680
Iteration: 293; Percent complete: 7.3%; Average loss: 3.8075
Iteration: 294; Percent complete: 7.3%; Average loss: 3.7223
Iteration: 295; Percent complete: 7.4%; Average loss: 3.8267
Iteration: 296; Percent complete: 7.4%; Average loss: 3.7995
Iteration: 297; Percent complete: 7.4%; Average loss: 3.6561
Iteration: 298; Percent complete: 7.4%; Average loss: 3.7578
Iteration: 299; Percent complete: 7.5%; Average loss: 3.7596
Iteration: 300; Percent complete: 7.5%; Average loss: 3.8997
Iteration: 301; Percent complete: 7.5%; Average loss: 3.9568
Iteration: 302; Percent complete: 7.5%; Average loss: 4.0026
Iteration: 303; Percent complete: 7.6%; Average loss: 3.7470
Iteration: 304; Percent complete: 7.6%; Average loss: 3.7811
Iteration: 305; Percent complete: 7.6%; Average loss: 3.9006
Iteration: 306; Percent complete: 7.6%; Average loss: 3.9926
Iteration: 307; Percent complete: 7.7%; Average loss: 4.1214
Iteration: 308; Percent complete: 7.7%; Average loss: 4.0965
Iteration: 309; Percent complete: 7.7%; Average loss: 4.0342
Iteration: 310; Percent complete: 7.8%; Average loss: 3.7160
Iteration: 311; Percent complete: 7.8%; Average loss: 3.8328
Iteration: 312; Percent complete: 7.8%; Average loss: 3.7148
Iteration: 313; Percent complete: 7.8%; Average loss: 3.7547
Iteration: 314; Percent complete: 7.8%; Average loss: 3.7535
Iteration: 315; Percent complete: 7.9%; Average loss: 3.8245
Iteration: 316; Percent complete: 7.9%; Average loss: 3.9072
Iteration: 317; Percent complete: 7.9%; Average loss: 3.7643
Iteration: 318; Percent complete: 8.0%; Average loss: 3.8957
Iteration: 319; Percent complete: 8.0%; Average loss: 4.0710
Iteration: 320; Percent complete: 8.0%; Average loss: 3.7270
Iteration: 321; Percent complete: 8.0%; Average loss: 3.7209
Iteration: 322; Percent complete: 8.1%; Average loss: 3.4785
Iteration: 323; Percent complete: 8.1%; Average loss: 3.7145
Iteration: 324; Percent complete: 8.1%; Average loss: 3.7348
Iteration: 325; Percent complete: 8.1%; Average loss: 3.8507
Iteration: 326; Percent complete: 8.2%; Average loss: 3.8203
Iteration: 327; Percent complete: 8.2%; Average loss: 3.7405
Iteration: 328; Percent complete: 8.2%; Average loss: 4.0654
Iteration: 329; Percent complete: 8.2%; Average loss: 3.6845
Iteration: 330; Percent complete: 8.2%; Average loss: 4.0475
Iteration: 331; Percent complete: 8.3%; Average loss: 3.7763
Iteration: 332; Percent complete: 8.3%; Average loss: 3.8882
Iteration: 333; Percent complete: 8.3%; Average loss: 3.9151
Iteration: 334; Percent complete: 8.3%; Average loss: 3.6505
Iteration: 335; Percent complete: 8.4%; Average loss: 3.9171
Iteration: 336; Percent complete: 8.4%; Average loss: 4.0568
Iteration: 337; Percent complete: 8.4%; Average loss: 3.8825
Iteration: 338; Percent complete: 8.5%; Average loss: 3.7738
Iteration: 339; Percent complete: 8.5%; Average loss: 3.9051
Iteration: 340; Percent complete: 8.5%; Average loss: 3.7872
Iteration: 341; Percent complete: 8.5%; Average loss: 3.9147
Iteration: 342; Percent complete: 8.6%; Average loss: 3.9641
Iteration: 343; Percent complete: 8.6%; Average loss: 4.0947
Iteration: 344; Percent complete: 8.6%; Average loss: 3.8178
Iteration: 345; Percent complete: 8.6%; Average loss: 3.9323
Iteration: 346; Percent complete: 8.6%; Average loss: 3.9316
Iteration: 347; Percent complete: 8.7%; Average loss: 3.7276
Iteration: 348; Percent complete: 8.7%; Average loss: 3.9878
Iteration: 349; Percent complete: 8.7%; Average loss: 3.9933
Iteration: 350; Percent complete: 8.8%; Average loss: 3.9107
Iteration: 351; Percent complete: 8.8%; Average loss: 3.7890
Iteration: 352; Percent complete: 8.8%; Average loss: 3.7396
Iteration: 353; Percent complete: 8.8%; Average loss: 3.7510
Iteration: 354; Percent complete: 8.8%; Average loss: 3.8825
Iteration: 355; Percent complete: 8.9%; Average loss: 3.5435
Iteration: 356; Percent complete: 8.9%; Average loss: 3.9651
Iteration: 357; Percent complete: 8.9%; Average loss: 3.8011
Iteration: 358; Percent complete: 8.9%; Average loss: 3.8180
Iteration: 359; Percent complete: 9.0%; Average loss: 3.8486
Iteration: 360; Percent complete: 9.0%; Average loss: 3.7820
Iteration: 361; Percent complete: 9.0%; Average loss: 3.8028
Iteration: 362; Percent complete: 9.0%; Average loss: 3.8048
Iteration: 363; Percent complete: 9.1%; Average loss: 3.8492
Iteration: 364; Percent complete: 9.1%; Average loss: 3.7504
Iteration: 365; Percent complete: 9.1%; Average loss: 3.7380
Iteration: 366; Percent complete: 9.2%; Average loss: 3.8352
Iteration: 367; Percent complete: 9.2%; Average loss: 3.6736
Iteration: 368; Percent complete: 9.2%; Average loss: 4.0574
Iteration: 369; Percent complete: 9.2%; Average loss: 3.8064
Iteration: 370; Percent complete: 9.2%; Average loss: 3.8930
Iteration: 371; Percent complete: 9.3%; Average loss: 4.0516
Iteration: 372; Percent complete: 9.3%; Average loss: 4.0612
Iteration: 373; Percent complete: 9.3%; Average loss: 3.8327
Iteration: 374; Percent complete: 9.3%; Average loss: 3.7477
Iteration: 375; Percent complete: 9.4%; Average loss: 3.6422
Iteration: 376; Percent complete: 9.4%; Average loss: 3.6533
Iteration: 377; Percent complete: 9.4%; Average loss: 3.8207
Iteration: 378; Percent complete: 9.4%; Average loss: 3.4329
Iteration: 379; Percent complete: 9.5%; Average loss: 3.5905
Iteration: 380; Percent complete: 9.5%; Average loss: 3.9740
Iteration: 381; Percent complete: 9.5%; Average loss: 3.9518
Iteration: 382; Percent complete: 9.6%; Average loss: 3.9425
Iteration: 383; Percent complete: 9.6%; Average loss: 3.9058
Iteration: 384; Percent complete: 9.6%; Average loss: 3.8163
Iteration: 385; Percent complete: 9.6%; Average loss: 3.8572
Iteration: 386; Percent complete: 9.7%; Average loss: 3.8682
Iteration: 387; Percent complete: 9.7%; Average loss: 3.6265
Iteration: 388; Percent complete: 9.7%; Average loss: 3.8442
Iteration: 389; Percent complete: 9.7%; Average loss: 3.8259
Iteration: 390; Percent complete: 9.8%; Average loss: 3.8850
Iteration: 391; Percent complete: 9.8%; Average loss: 3.8230
Iteration: 392; Percent complete: 9.8%; Average loss: 3.9410
Iteration: 393; Percent complete: 9.8%; Average loss: 3.9234
Iteration: 394; Percent complete: 9.8%; Average loss: 4.2334
Iteration: 395; Percent complete: 9.9%; Average loss: 3.9407
Iteration: 396; Percent complete: 9.9%; Average loss: 3.8385
Iteration: 397; Percent complete: 9.9%; Average loss: 3.8594
Iteration: 398; Percent complete: 10.0%; Average loss: 3.6778
Iteration: 399; Percent complete: 10.0%; Average loss: 3.6240
Iteration: 400; Percent complete: 10.0%; Average loss: 3.8860
Iteration: 401; Percent complete: 10.0%; Average loss: 3.6828
Iteration: 402; Percent complete: 10.1%; Average loss: 3.7690
Iteration: 403; Percent complete: 10.1%; Average loss: 3.8818
Iteration: 404; Percent complete: 10.1%; Average loss: 3.7585
Iteration: 405; Percent complete: 10.1%; Average loss: 3.7906
Iteration: 406; Percent complete: 10.2%; Average loss: 3.7110
Iteration: 407; Percent complete: 10.2%; Average loss: 3.8027
Iteration: 408; Percent complete: 10.2%; Average loss: 3.9051
Iteration: 409; Percent complete: 10.2%; Average loss: 3.6447
Iteration: 410; Percent complete: 10.2%; Average loss: 3.6421
Iteration: 411; Percent complete: 10.3%; Average loss: 3.6993
Iteration: 412; Percent complete: 10.3%; Average loss: 3.8673
Iteration: 413; Percent complete: 10.3%; Average loss: 3.9234
Iteration: 414; Percent complete: 10.3%; Average loss: 3.9401
Iteration: 415; Percent complete: 10.4%; Average loss: 3.8330
Iteration: 416; Percent complete: 10.4%; Average loss: 3.3808
Iteration: 417; Percent complete: 10.4%; Average loss: 3.8343
Iteration: 418; Percent complete: 10.4%; Average loss: 3.7285
Iteration: 419; Percent complete: 10.5%; Average loss: 3.5221
Iteration: 420; Percent complete: 10.5%; Average loss: 3.8533
Iteration: 421; Percent complete: 10.5%; Average loss: 3.6881
Iteration: 422; Percent complete: 10.5%; Average loss: 3.5494
Iteration: 423; Percent complete: 10.6%; Average loss: 3.7350
Iteration: 424; Percent complete: 10.6%; Average loss: 3.9166
Iteration: 425; Percent complete: 10.6%; Average loss: 4.0079
Iteration: 426; Percent complete: 10.7%; Average loss: 3.9489
Iteration: 427; Percent complete: 10.7%; Average loss: 3.7437
Iteration: 428; Percent complete: 10.7%; Average loss: 3.8960
Iteration: 429; Percent complete: 10.7%; Average loss: 3.7162
Iteration: 430; Percent complete: 10.8%; Average loss: 3.9231
Iteration: 431; Percent complete: 10.8%; Average loss: 3.9471
Iteration: 432; Percent complete: 10.8%; Average loss: 4.1242
Iteration: 433; Percent complete: 10.8%; Average loss: 3.8358
Iteration: 434; Percent complete: 10.8%; Average loss: 3.9054
Iteration: 435; Percent complete: 10.9%; Average loss: 3.8679
Iteration: 436; Percent complete: 10.9%; Average loss: 3.7822
Iteration: 437; Percent complete: 10.9%; Average loss: 3.5906
Iteration: 438; Percent complete: 10.9%; Average loss: 3.6033
Iteration: 439; Percent complete: 11.0%; Average loss: 3.8030
Iteration: 440; Percent complete: 11.0%; Average loss: 3.8636
Iteration: 441; Percent complete: 11.0%; Average loss: 3.8597
Iteration: 442; Percent complete: 11.1%; Average loss: 3.7960
Iteration: 443; Percent complete: 11.1%; Average loss: 3.4849
Iteration: 444; Percent complete: 11.1%; Average loss: 3.8480
Iteration: 445; Percent complete: 11.1%; Average loss: 4.0131
Iteration: 446; Percent complete: 11.2%; Average loss: 3.8628
Iteration: 447; Percent complete: 11.2%; Average loss: 3.8610
Iteration: 448; Percent complete: 11.2%; Average loss: 3.9905
Iteration: 449; Percent complete: 11.2%; Average loss: 3.9158
Iteration: 450; Percent complete: 11.2%; Average loss: 3.6937
Iteration: 451; Percent complete: 11.3%; Average loss: 3.9597
Iteration: 452; Percent complete: 11.3%; Average loss: 3.6904
Iteration: 453; Percent complete: 11.3%; Average loss: 3.6006
Iteration: 454; Percent complete: 11.3%; Average loss: 3.7524
Iteration: 455; Percent complete: 11.4%; Average loss: 3.6415
Iteration: 456; Percent complete: 11.4%; Average loss: 3.8229
Iteration: 457; Percent complete: 11.4%; Average loss: 3.6585
Iteration: 458; Percent complete: 11.5%; Average loss: 4.0009
Iteration: 459; Percent complete: 11.5%; Average loss: 3.8799
Iteration: 460; Percent complete: 11.5%; Average loss: 3.7188
Iteration: 461; Percent complete: 11.5%; Average loss: 3.8392
Iteration: 462; Percent complete: 11.6%; Average loss: 3.7278
Iteration: 463; Percent complete: 11.6%; Average loss: 3.5210
Iteration: 464; Percent complete: 11.6%; Average loss: 3.7879
Iteration: 465; Percent complete: 11.6%; Average loss: 3.8222
Iteration: 466; Percent complete: 11.7%; Average loss: 3.6145
Iteration: 467; Percent complete: 11.7%; Average loss: 3.5866
Iteration: 468; Percent complete: 11.7%; Average loss: 3.9915
Iteration: 469; Percent complete: 11.7%; Average loss: 3.8805
Iteration: 470; Percent complete: 11.8%; Average loss: 3.6866
Iteration: 471; Percent complete: 11.8%; Average loss: 3.7208
Iteration: 472; Percent complete: 11.8%; Average loss: 3.7212
Iteration: 473; Percent complete: 11.8%; Average loss: 3.3681
Iteration: 474; Percent complete: 11.8%; Average loss: 3.8062
Iteration: 475; Percent complete: 11.9%; Average loss: 3.8384
Iteration: 476; Percent complete: 11.9%; Average loss: 3.7545
Iteration: 477; Percent complete: 11.9%; Average loss: 3.8431
Iteration: 478; Percent complete: 11.9%; Average loss: 3.8787
Iteration: 479; Percent complete: 12.0%; Average loss: 3.7320
Iteration: 480; Percent complete: 12.0%; Average loss: 3.6197
Iteration: 481; Percent complete: 12.0%; Average loss: 3.7255
Iteration: 482; Percent complete: 12.0%; Average loss: 3.7385
Iteration: 483; Percent complete: 12.1%; Average loss: 3.8009
Iteration: 484; Percent complete: 12.1%; Average loss: 3.8282
Iteration: 485; Percent complete: 12.1%; Average loss: 3.7278
Iteration: 486; Percent complete: 12.2%; Average loss: 4.0084
Iteration: 487; Percent complete: 12.2%; Average loss: 4.0919
Iteration: 488; Percent complete: 12.2%; Average loss: 3.7436
Iteration: 489; Percent complete: 12.2%; Average loss: 3.9657
Iteration: 490; Percent complete: 12.2%; Average loss: 3.4575
Iteration: 491; Percent complete: 12.3%; Average loss: 4.0489
Iteration: 492; Percent complete: 12.3%; Average loss: 3.6907
Iteration: 493; Percent complete: 12.3%; Average loss: 3.6426
Iteration: 494; Percent complete: 12.3%; Average loss: 3.7034
Iteration: 495; Percent complete: 12.4%; Average loss: 3.7559
Iteration: 496; Percent complete: 12.4%; Average loss: 3.8602
Iteration: 497; Percent complete: 12.4%; Average loss: 3.7122
Iteration: 498; Percent complete: 12.4%; Average loss: 3.4879
Iteration: 499; Percent complete: 12.5%; Average loss: 3.9532
Iteration: 500; Percent complete: 12.5%; Average loss: 3.6458
Iteration: 501; Percent complete: 12.5%; Average loss: 3.9125
Iteration: 502; Percent complete: 12.6%; Average loss: 3.6115
Iteration: 503; Percent complete: 12.6%; Average loss: 3.9949
Iteration: 504; Percent complete: 12.6%; Average loss: 3.8843
Iteration: 505; Percent complete: 12.6%; Average loss: 3.8103
Iteration: 506; Percent complete: 12.7%; Average loss: 3.8098
Iteration: 507; Percent complete: 12.7%; Average loss: 3.6831
Iteration: 508; Percent complete: 12.7%; Average loss: 3.8033
Iteration: 509; Percent complete: 12.7%; Average loss: 3.7205
Iteration: 510; Percent complete: 12.8%; Average loss: 3.9389
Iteration: 511; Percent complete: 12.8%; Average loss: 3.6989
Iteration: 512; Percent complete: 12.8%; Average loss: 3.5280
Iteration: 513; Percent complete: 12.8%; Average loss: 4.0792
Iteration: 514; Percent complete: 12.8%; Average loss: 3.7593
Iteration: 515; Percent complete: 12.9%; Average loss: 3.8754
Iteration: 516; Percent complete: 12.9%; Average loss: 3.7610
Iteration: 517; Percent complete: 12.9%; Average loss: 3.8430
Iteration: 518; Percent complete: 13.0%; Average loss: 3.5974
Iteration: 519; Percent complete: 13.0%; Average loss: 3.9012
Iteration: 520; Percent complete: 13.0%; Average loss: 3.8593
Iteration: 521; Percent complete: 13.0%; Average loss: 3.7417
Iteration: 522; Percent complete: 13.1%; Average loss: 3.5340
Iteration: 523; Percent complete: 13.1%; Average loss: 3.6719
Iteration: 524; Percent complete: 13.1%; Average loss: 3.6003
Iteration: 525; Percent complete: 13.1%; Average loss: 3.7229
Iteration: 526; Percent complete: 13.2%; Average loss: 3.5650
Iteration: 527; Percent complete: 13.2%; Average loss: 3.7647
Iteration: 528; Percent complete: 13.2%; Average loss: 3.7593
Iteration: 529; Percent complete: 13.2%; Average loss: 3.7561
Iteration: 530; Percent complete: 13.2%; Average loss: 3.7417
Iteration: 531; Percent complete: 13.3%; Average loss: 3.7470
Iteration: 532; Percent complete: 13.3%; Average loss: 3.6787
Iteration: 533; Percent complete: 13.3%; Average loss: 3.7203
Iteration: 534; Percent complete: 13.4%; Average loss: 3.6793
Iteration: 535; Percent complete: 13.4%; Average loss: 3.7590
Iteration: 536; Percent complete: 13.4%; Average loss: 4.0041
Iteration: 537; Percent complete: 13.4%; Average loss: 3.6489
Iteration: 538; Percent complete: 13.5%; Average loss: 3.6827
Iteration: 539; Percent complete: 13.5%; Average loss: 3.8748
Iteration: 540; Percent complete: 13.5%; Average loss: 3.7092
Iteration: 541; Percent complete: 13.5%; Average loss: 3.6504
Iteration: 542; Percent complete: 13.6%; Average loss: 3.4808
Iteration: 543; Percent complete: 13.6%; Average loss: 3.6929
Iteration: 544; Percent complete: 13.6%; Average loss: 3.6196
Iteration: 545; Percent complete: 13.6%; Average loss: 3.7173
Iteration: 546; Percent complete: 13.7%; Average loss: 3.7434
Iteration: 547; Percent complete: 13.7%; Average loss: 3.6673
Iteration: 548; Percent complete: 13.7%; Average loss: 3.7675
Iteration: 549; Percent complete: 13.7%; Average loss: 3.8201
Iteration: 550; Percent complete: 13.8%; Average loss: 3.8742
Iteration: 551; Percent complete: 13.8%; Average loss: 3.6166
Iteration: 552; Percent complete: 13.8%; Average loss: 3.5572
Iteration: 553; Percent complete: 13.8%; Average loss: 4.0171
Iteration: 554; Percent complete: 13.9%; Average loss: 3.9146
Iteration: 555; Percent complete: 13.9%; Average loss: 3.5718
Iteration: 556; Percent complete: 13.9%; Average loss: 3.7938
Iteration: 557; Percent complete: 13.9%; Average loss: 3.9637
Iteration: 558; Percent complete: 14.0%; Average loss: 3.8853
Iteration: 559; Percent complete: 14.0%; Average loss: 3.8289
Iteration: 560; Percent complete: 14.0%; Average loss: 3.4595
Iteration: 561; Percent complete: 14.0%; Average loss: 3.6398
Iteration: 562; Percent complete: 14.1%; Average loss: 3.5241
Iteration: 563; Percent complete: 14.1%; Average loss: 3.8537
Iteration: 564; Percent complete: 14.1%; Average loss: 3.7320
Iteration: 565; Percent complete: 14.1%; Average loss: 3.7828
Iteration: 566; Percent complete: 14.1%; Average loss: 3.5636
Iteration: 567; Percent complete: 14.2%; Average loss: 3.8514
Iteration: 568; Percent complete: 14.2%; Average loss: 3.8252
Iteration: 569; Percent complete: 14.2%; Average loss: 3.6032
Iteration: 570; Percent complete: 14.2%; Average loss: 3.7650
Iteration: 571; Percent complete: 14.3%; Average loss: 3.6767
Iteration: 572; Percent complete: 14.3%; Average loss: 3.5332
Iteration: 573; Percent complete: 14.3%; Average loss: 3.5319
Iteration: 574; Percent complete: 14.3%; Average loss: 3.7146
Iteration: 575; Percent complete: 14.4%; Average loss: 3.5718
Iteration: 576; Percent complete: 14.4%; Average loss: 3.5036
Iteration: 577; Percent complete: 14.4%; Average loss: 3.5049
Iteration: 578; Percent complete: 14.4%; Average loss: 3.9189
Iteration: 579; Percent complete: 14.5%; Average loss: 3.7183
Iteration: 580; Percent complete: 14.5%; Average loss: 3.7066
Iteration: 581; Percent complete: 14.5%; Average loss: 3.8747
Iteration: 582; Percent complete: 14.5%; Average loss: 3.5322
Iteration: 583; Percent complete: 14.6%; Average loss: 3.6036
Iteration: 584; Percent complete: 14.6%; Average loss: 3.6537
Iteration: 585; Percent complete: 14.6%; Average loss: 3.6578
Iteration: 586; Percent complete: 14.6%; Average loss: 3.6955
Iteration: 587; Percent complete: 14.7%; Average loss: 3.6704
Iteration: 588; Percent complete: 14.7%; Average loss: 3.7085
Iteration: 589; Percent complete: 14.7%; Average loss: 3.8004
Iteration: 590; Percent complete: 14.8%; Average loss: 3.5787
Iteration: 591; Percent complete: 14.8%; Average loss: 3.8024
Iteration: 592; Percent complete: 14.8%; Average loss: 3.5939
Iteration: 593; Percent complete: 14.8%; Average loss: 3.8235
Iteration: 594; Percent complete: 14.8%; Average loss: 3.3676
Iteration: 595; Percent complete: 14.9%; Average loss: 3.7688
Iteration: 596; Percent complete: 14.9%; Average loss: 3.7432
Iteration: 597; Percent complete: 14.9%; Average loss: 3.4481
Iteration: 598; Percent complete: 14.9%; Average loss: 3.6986
Iteration: 599; Percent complete: 15.0%; Average loss: 3.7346
Iteration: 600; Percent complete: 15.0%; Average loss: 3.4718
Iteration: 601; Percent complete: 15.0%; Average loss: 3.6587
Iteration: 602; Percent complete: 15.0%; Average loss: 3.7548
Iteration: 603; Percent complete: 15.1%; Average loss: 3.7049
Iteration: 604; Percent complete: 15.1%; Average loss: 3.2093
Iteration: 605; Percent complete: 15.1%; Average loss: 3.6065
Iteration: 606; Percent complete: 15.2%; Average loss: 3.3308
Iteration: 607; Percent complete: 15.2%; Average loss: 3.6990
Iteration: 608; Percent complete: 15.2%; Average loss: 3.5223
Iteration: 609; Percent complete: 15.2%; Average loss: 3.8079
Iteration: 610; Percent complete: 15.2%; Average loss: 3.5955
Iteration: 611; Percent complete: 15.3%; Average loss: 3.7687
Iteration: 612; Percent complete: 15.3%; Average loss: 3.7601
Iteration: 613; Percent complete: 15.3%; Average loss: 3.8626
Iteration: 614; Percent complete: 15.3%; Average loss: 3.7333
Iteration: 615; Percent complete: 15.4%; Average loss: 3.5732
Iteration: 616; Percent complete: 15.4%; Average loss: 3.7131
Iteration: 617; Percent complete: 15.4%; Average loss: 3.7711
Iteration: 618; Percent complete: 15.4%; Average loss: 3.7300
Iteration: 619; Percent complete: 15.5%; Average loss: 3.5092
Iteration: 620; Percent complete: 15.5%; Average loss: 3.6533
Iteration: 621; Percent complete: 15.5%; Average loss: 3.5854
Iteration: 622; Percent complete: 15.6%; Average loss: 3.5281
Iteration: 623; Percent complete: 15.6%; Average loss: 3.6190
Iteration: 624; Percent complete: 15.6%; Average loss: 3.6556
Iteration: 625; Percent complete: 15.6%; Average loss: 3.5007
Iteration: 626; Percent complete: 15.7%; Average loss: 3.5903
Iteration: 627; Percent complete: 15.7%; Average loss: 3.4510
Iteration: 628; Percent complete: 15.7%; Average loss: 3.8944
Iteration: 629; Percent complete: 15.7%; Average loss: 3.6732
Iteration: 630; Percent complete: 15.8%; Average loss: 3.6152
Iteration: 631; Percent complete: 15.8%; Average loss: 3.6104
Iteration: 632; Percent complete: 15.8%; Average loss: 3.4904
Iteration: 633; Percent complete: 15.8%; Average loss: 3.4541
Iteration: 634; Percent complete: 15.8%; Average loss: 3.7905
Iteration: 635; Percent complete: 15.9%; Average loss: 3.5506
Iteration: 636; Percent complete: 15.9%; Average loss: 3.4359
Iteration: 637; Percent complete: 15.9%; Average loss: 3.4420
Iteration: 638; Percent complete: 16.0%; Average loss: 3.6890
Iteration: 639; Percent complete: 16.0%; Average loss: 3.6600
Iteration: 640; Percent complete: 16.0%; Average loss: 3.4800
Iteration: 641; Percent complete: 16.0%; Average loss: 3.7107
Iteration: 642; Percent complete: 16.1%; Average loss: 3.7078
Iteration: 643; Percent complete: 16.1%; Average loss: 3.5934
Iteration: 644; Percent complete: 16.1%; Average loss: 3.7197
Iteration: 645; Percent complete: 16.1%; Average loss: 3.7483
Iteration: 646; Percent complete: 16.2%; Average loss: 3.6312
Iteration: 647; Percent complete: 16.2%; Average loss: 3.8460
Iteration: 648; Percent complete: 16.2%; Average loss: 3.4899
Iteration: 649; Percent complete: 16.2%; Average loss: 4.0365
Iteration: 650; Percent complete: 16.2%; Average loss: 3.7538
Iteration: 651; Percent complete: 16.3%; Average loss: 3.7258
Iteration: 652; Percent complete: 16.3%; Average loss: 3.6621
Iteration: 653; Percent complete: 16.3%; Average loss: 3.4542
Iteration: 654; Percent complete: 16.4%; Average loss: 3.5121
Iteration: 655; Percent complete: 16.4%; Average loss: 3.5401
Iteration: 656; Percent complete: 16.4%; Average loss: 3.4285
Iteration: 657; Percent complete: 16.4%; Average loss: 3.5282
Iteration: 658; Percent complete: 16.4%; Average loss: 3.6713
Iteration: 659; Percent complete: 16.5%; Average loss: 4.0381
Iteration: 660; Percent complete: 16.5%; Average loss: 3.6986
Iteration: 661; Percent complete: 16.5%; Average loss: 3.5886
Iteration: 662; Percent complete: 16.6%; Average loss: 3.6443
Iteration: 663; Percent complete: 16.6%; Average loss: 3.5688
Iteration: 664; Percent complete: 16.6%; Average loss: 3.5405
Iteration: 665; Percent complete: 16.6%; Average loss: 3.6543
Iteration: 666; Percent complete: 16.7%; Average loss: 3.7462
Iteration: 667; Percent complete: 16.7%; Average loss: 3.7083
Iteration: 668; Percent complete: 16.7%; Average loss: 3.4410
Iteration: 669; Percent complete: 16.7%; Average loss: 3.6258
Iteration: 670; Percent complete: 16.8%; Average loss: 3.7833
Iteration: 671; Percent complete: 16.8%; Average loss: 3.4843
Iteration: 672; Percent complete: 16.8%; Average loss: 3.5646
Iteration: 673; Percent complete: 16.8%; Average loss: 3.7392
Iteration: 674; Percent complete: 16.9%; Average loss: 3.5658
Iteration: 675; Percent complete: 16.9%; Average loss: 3.8978
Iteration: 676; Percent complete: 16.9%; Average loss: 3.5009
Iteration: 677; Percent complete: 16.9%; Average loss: 3.5670
Iteration: 678; Percent complete: 17.0%; Average loss: 3.8465
Iteration: 679; Percent complete: 17.0%; Average loss: 3.7223
Iteration: 680; Percent complete: 17.0%; Average loss: 3.5338
Iteration: 681; Percent complete: 17.0%; Average loss: 3.6177
Iteration: 682; Percent complete: 17.1%; Average loss: 3.7310
Iteration: 683; Percent complete: 17.1%; Average loss: 3.6370
Iteration: 684; Percent complete: 17.1%; Average loss: 3.3677
Iteration: 685; Percent complete: 17.1%; Average loss: 3.5128
Iteration: 686; Percent complete: 17.2%; Average loss: 3.6903
Iteration: 687; Percent complete: 17.2%; Average loss: 3.8982
Iteration: 688; Percent complete: 17.2%; Average loss: 3.3660
Iteration: 689; Percent complete: 17.2%; Average loss: 3.5925
Iteration: 690; Percent complete: 17.2%; Average loss: 3.5782
Iteration: 691; Percent complete: 17.3%; Average loss: 3.5923
Iteration: 692; Percent complete: 17.3%; Average loss: 3.6499
Iteration: 693; Percent complete: 17.3%; Average loss: 3.6857
Iteration: 694; Percent complete: 17.3%; Average loss: 3.6548
Iteration: 695; Percent complete: 17.4%; Average loss: 3.7770
Iteration: 696; Percent complete: 17.4%; Average loss: 3.4175
Iteration: 697; Percent complete: 17.4%; Average loss: 3.5526
Iteration: 698; Percent complete: 17.4%; Average loss: 3.8038
Iteration: 699; Percent complete: 17.5%; Average loss: 3.3770
Iteration: 700; Percent complete: 17.5%; Average loss: 4.0563
Iteration: 701; Percent complete: 17.5%; Average loss: 3.4329
Iteration: 702; Percent complete: 17.5%; Average loss: 3.9182
Iteration: 703; Percent complete: 17.6%; Average loss: 3.7151
Iteration: 704; Percent complete: 17.6%; Average loss: 3.5383
Iteration: 705; Percent complete: 17.6%; Average loss: 3.8138
Iteration: 706; Percent complete: 17.6%; Average loss: 3.6820
Iteration: 707; Percent complete: 17.7%; Average loss: 3.6907
Iteration: 708; Percent complete: 17.7%; Average loss: 3.4481
Iteration: 709; Percent complete: 17.7%; Average loss: 3.5396
Iteration: 710; Percent complete: 17.8%; Average loss: 3.5293
Iteration: 711; Percent complete: 17.8%; Average loss: 3.6908
Iteration: 712; Percent complete: 17.8%; Average loss: 3.8293
Iteration: 713; Percent complete: 17.8%; Average loss: 3.5032
Iteration: 714; Percent complete: 17.8%; Average loss: 3.7462
Iteration: 715; Percent complete: 17.9%; Average loss: 3.5560
Iteration: 716; Percent complete: 17.9%; Average loss: 3.5956
Iteration: 717; Percent complete: 17.9%; Average loss: 3.6488
Iteration: 718; Percent complete: 17.9%; Average loss: 3.8754
Iteration: 719; Percent complete: 18.0%; Average loss: 3.6256
Iteration: 720; Percent complete: 18.0%; Average loss: 3.7641
Iteration: 721; Percent complete: 18.0%; Average loss: 3.6532
Iteration: 722; Percent complete: 18.1%; Average loss: 3.2401
Iteration: 723; Percent complete: 18.1%; Average loss: 3.8165
Iteration: 724; Percent complete: 18.1%; Average loss: 3.4654
Iteration: 725; Percent complete: 18.1%; Average loss: 4.0274
Iteration: 726; Percent complete: 18.1%; Average loss: 3.7026
Iteration: 727; Percent complete: 18.2%; Average loss: 3.7572
Iteration: 728; Percent complete: 18.2%; Average loss: 3.3975
Iteration: 729; Percent complete: 18.2%; Average loss: 3.7388
Iteration: 730; Percent complete: 18.2%; Average loss: 3.4375
Iteration: 731; Percent complete: 18.3%; Average loss: 3.5835
Iteration: 732; Percent complete: 18.3%; Average loss: 3.6253
Iteration: 733; Percent complete: 18.3%; Average loss: 3.7989
Iteration: 734; Percent complete: 18.4%; Average loss: 3.6914
Iteration: 735; Percent complete: 18.4%; Average loss: 3.6005
Iteration: 736; Percent complete: 18.4%; Average loss: 3.4289
Iteration: 737; Percent complete: 18.4%; Average loss: 3.4988
Iteration: 738; Percent complete: 18.4%; Average loss: 3.7093
Iteration: 739; Percent complete: 18.5%; Average loss: 3.7213
Iteration: 740; Percent complete: 18.5%; Average loss: 3.8080
Iteration: 741; Percent complete: 18.5%; Average loss: 3.4712
Iteration: 742; Percent complete: 18.6%; Average loss: 3.6047
Iteration: 743; Percent complete: 18.6%; Average loss: 3.6664
Iteration: 744; Percent complete: 18.6%; Average loss: 3.6169
Iteration: 745; Percent complete: 18.6%; Average loss: 3.4970
Iteration: 746; Percent complete: 18.6%; Average loss: 3.4621
Iteration: 747; Percent complete: 18.7%; Average loss: 3.5196
Iteration: 748; Percent complete: 18.7%; Average loss: 3.5564
Iteration: 749; Percent complete: 18.7%; Average loss: 3.6707
Iteration: 750; Percent complete: 18.8%; Average loss: 3.5537
Iteration: 751; Percent complete: 18.8%; Average loss: 3.5051
Iteration: 752; Percent complete: 18.8%; Average loss: 3.6104
Iteration: 753; Percent complete: 18.8%; Average loss: 3.7524
Iteration: 754; Percent complete: 18.9%; Average loss: 3.6813
Iteration: 755; Percent complete: 18.9%; Average loss: 3.6766
Iteration: 756; Percent complete: 18.9%; Average loss: 3.4280
Iteration: 757; Percent complete: 18.9%; Average loss: 3.6192
Iteration: 758; Percent complete: 18.9%; Average loss: 3.4161
Iteration: 759; Percent complete: 19.0%; Average loss: 3.2916
Iteration: 760; Percent complete: 19.0%; Average loss: 3.6394
Iteration: 761; Percent complete: 19.0%; Average loss: 3.7242
Iteration: 762; Percent complete: 19.1%; Average loss: 3.6615
Iteration: 763; Percent complete: 19.1%; Average loss: 3.3873
Iteration: 764; Percent complete: 19.1%; Average loss: 3.6179
Iteration: 765; Percent complete: 19.1%; Average loss: 3.4073
Iteration: 766; Percent complete: 19.1%; Average loss: 3.7181
Iteration: 767; Percent complete: 19.2%; Average loss: 3.5184
Iteration: 768; Percent complete: 19.2%; Average loss: 3.4103
Iteration: 769; Percent complete: 19.2%; Average loss: 3.7307
Iteration: 770; Percent complete: 19.2%; Average loss: 3.7829
Iteration: 771; Percent complete: 19.3%; Average loss: 3.7181
Iteration: 772; Percent complete: 19.3%; Average loss: 3.6730
Iteration: 773; Percent complete: 19.3%; Average loss: 3.6195
Iteration: 774; Percent complete: 19.4%; Average loss: 3.8237
Iteration: 775; Percent complete: 19.4%; Average loss: 3.4700
Iteration: 776; Percent complete: 19.4%; Average loss: 3.7463
Iteration: 777; Percent complete: 19.4%; Average loss: 3.4738
Iteration: 778; Percent complete: 19.4%; Average loss: 3.5392
Iteration: 779; Percent complete: 19.5%; Average loss: 3.7223
Iteration: 780; Percent complete: 19.5%; Average loss: 3.4202
Iteration: 781; Percent complete: 19.5%; Average loss: 3.5589
Iteration: 782; Percent complete: 19.6%; Average loss: 3.3978
Iteration: 783; Percent complete: 19.6%; Average loss: 3.6310
Iteration: 784; Percent complete: 19.6%; Average loss: 3.6410
Iteration: 785; Percent complete: 19.6%; Average loss: 3.4858
Iteration: 786; Percent complete: 19.7%; Average loss: 3.5107
Iteration: 787; Percent complete: 19.7%; Average loss: 3.5278
Iteration: 788; Percent complete: 19.7%; Average loss: 3.6712
Iteration: 789; Percent complete: 19.7%; Average loss: 3.5095
Iteration: 790; Percent complete: 19.8%; Average loss: 3.5808
Iteration: 791; Percent complete: 19.8%; Average loss: 3.7019
Iteration: 792; Percent complete: 19.8%; Average loss: 3.7260
Iteration: 793; Percent complete: 19.8%; Average loss: 3.3567
Iteration: 794; Percent complete: 19.9%; Average loss: 3.1836
Iteration: 795; Percent complete: 19.9%; Average loss: 3.2264
Iteration: 796; Percent complete: 19.9%; Average loss: 3.3826
Iteration: 797; Percent complete: 19.9%; Average loss: 3.7373
Iteration: 798; Percent complete: 20.0%; Average loss: 3.7478
Iteration: 799; Percent complete: 20.0%; Average loss: 3.6582
Iteration: 800; Percent complete: 20.0%; Average loss: 3.4829
Iteration: 801; Percent complete: 20.0%; Average loss: 3.7317
Iteration: 802; Percent complete: 20.1%; Average loss: 3.7348
Iteration: 803; Percent complete: 20.1%; Average loss: 3.2806
Iteration: 804; Percent complete: 20.1%; Average loss: 3.6747
Iteration: 805; Percent complete: 20.1%; Average loss: 3.6565
Iteration: 806; Percent complete: 20.2%; Average loss: 3.7577
Iteration: 807; Percent complete: 20.2%; Average loss: 3.8098
Iteration: 808; Percent complete: 20.2%; Average loss: 3.5165
Iteration: 809; Percent complete: 20.2%; Average loss: 3.7430
Iteration: 810; Percent complete: 20.2%; Average loss: 3.4078
Iteration: 811; Percent complete: 20.3%; Average loss: 3.4364
Iteration: 812; Percent complete: 20.3%; Average loss: 3.6790
Iteration: 813; Percent complete: 20.3%; Average loss: 3.7581
Iteration: 814; Percent complete: 20.3%; Average loss: 3.2629
Iteration: 815; Percent complete: 20.4%; Average loss: 3.3046
Iteration: 816; Percent complete: 20.4%; Average loss: 3.5667
Iteration: 817; Percent complete: 20.4%; Average loss: 3.3053
Iteration: 818; Percent complete: 20.4%; Average loss: 3.6555
Iteration: 819; Percent complete: 20.5%; Average loss: 3.3028
Iteration: 820; Percent complete: 20.5%; Average loss: 3.6363
Iteration: 821; Percent complete: 20.5%; Average loss: 3.3632
Iteration: 822; Percent complete: 20.5%; Average loss: 3.5860
Iteration: 823; Percent complete: 20.6%; Average loss: 3.7367
Iteration: 824; Percent complete: 20.6%; Average loss: 3.5889
Iteration: 825; Percent complete: 20.6%; Average loss: 3.4103
Iteration: 826; Percent complete: 20.6%; Average loss: 3.6657
Iteration: 827; Percent complete: 20.7%; Average loss: 3.5277
Iteration: 828; Percent complete: 20.7%; Average loss: 3.3191
Iteration: 829; Percent complete: 20.7%; Average loss: 3.7715
Iteration: 830; Percent complete: 20.8%; Average loss: 3.5291
Iteration: 831; Percent complete: 20.8%; Average loss: 3.3832
Iteration: 832; Percent complete: 20.8%; Average loss: 3.0308
Iteration: 833; Percent complete: 20.8%; Average loss: 3.4990
Iteration: 834; Percent complete: 20.8%; Average loss: 3.7382
Iteration: 835; Percent complete: 20.9%; Average loss: 3.7449
Iteration: 836; Percent complete: 20.9%; Average loss: 3.7412
Iteration: 837; Percent complete: 20.9%; Average loss: 3.6603
Iteration: 838; Percent complete: 20.9%; Average loss: 3.8440
Iteration: 839; Percent complete: 21.0%; Average loss: 3.6435
Iteration: 840; Percent complete: 21.0%; Average loss: 3.4516
Iteration: 841; Percent complete: 21.0%; Average loss: 3.8637
Iteration: 842; Percent complete: 21.1%; Average loss: 3.6422
Iteration: 843; Percent complete: 21.1%; Average loss: 3.4386
Iteration: 844; Percent complete: 21.1%; Average loss: 3.4752
Iteration: 845; Percent complete: 21.1%; Average loss: 3.5514
Iteration: 846; Percent complete: 21.1%; Average loss: 3.5743
Iteration: 847; Percent complete: 21.2%; Average loss: 3.5673
Iteration: 848; Percent complete: 21.2%; Average loss: 3.4245
Iteration: 849; Percent complete: 21.2%; Average loss: 3.3829
Iteration: 850; Percent complete: 21.2%; Average loss: 3.3965
Iteration: 851; Percent complete: 21.3%; Average loss: 3.3845
Iteration: 852; Percent complete: 21.3%; Average loss: 3.6097
Iteration: 853; Percent complete: 21.3%; Average loss: 3.6600
Iteration: 854; Percent complete: 21.3%; Average loss: 3.5258
Iteration: 855; Percent complete: 21.4%; Average loss: 3.5818
Iteration: 856; Percent complete: 21.4%; Average loss: 3.3276
Iteration: 857; Percent complete: 21.4%; Average loss: 3.4141
Iteration: 858; Percent complete: 21.4%; Average loss: 3.8072
Iteration: 859; Percent complete: 21.5%; Average loss: 3.6123
Iteration: 860; Percent complete: 21.5%; Average loss: 3.5659
Iteration: 861; Percent complete: 21.5%; Average loss: 3.5137
Iteration: 862; Percent complete: 21.6%; Average loss: 3.6170
Iteration: 863; Percent complete: 21.6%; Average loss: 3.6421
Iteration: 864; Percent complete: 21.6%; Average loss: 3.5230
Iteration: 865; Percent complete: 21.6%; Average loss: 3.7144
Iteration: 866; Percent complete: 21.6%; Average loss: 3.3128
Iteration: 867; Percent complete: 21.7%; Average loss: 3.5372
Iteration: 868; Percent complete: 21.7%; Average loss: 3.1930
Iteration: 869; Percent complete: 21.7%; Average loss: 3.5795
Iteration: 870; Percent complete: 21.8%; Average loss: 3.2554
Iteration: 871; Percent complete: 21.8%; Average loss: 3.6301
Iteration: 872; Percent complete: 21.8%; Average loss: 3.4322
Iteration: 873; Percent complete: 21.8%; Average loss: 3.6638
Iteration: 874; Percent complete: 21.9%; Average loss: 3.5652
Iteration: 875; Percent complete: 21.9%; Average loss: 3.5918
Iteration: 876; Percent complete: 21.9%; Average loss: 3.4820
Iteration: 877; Percent complete: 21.9%; Average loss: 3.4527
Iteration: 878; Percent complete: 21.9%; Average loss: 3.7651
Iteration: 879; Percent complete: 22.0%; Average loss: 3.5904
Iteration: 880; Percent complete: 22.0%; Average loss: 3.4648
Iteration: 881; Percent complete: 22.0%; Average loss: 3.6884
Iteration: 882; Percent complete: 22.1%; Average loss: 3.4921
Iteration: 883; Percent complete: 22.1%; Average loss: 3.2869
Iteration: 884; Percent complete: 22.1%; Average loss: 3.5554
Iteration: 885; Percent complete: 22.1%; Average loss: 3.6877
Iteration: 886; Percent complete: 22.1%; Average loss: 3.5050
Iteration: 887; Percent complete: 22.2%; Average loss: 3.3625
Iteration: 888; Percent complete: 22.2%; Average loss: 3.4408
Iteration: 889; Percent complete: 22.2%; Average loss: 3.7464
Iteration: 890; Percent complete: 22.2%; Average loss: 3.2558
Iteration: 891; Percent complete: 22.3%; Average loss: 3.4290
Iteration: 892; Percent complete: 22.3%; Average loss: 3.8551
Iteration: 893; Percent complete: 22.3%; Average loss: 3.5231
Iteration: 894; Percent complete: 22.4%; Average loss: 3.6230
Iteration: 895; Percent complete: 22.4%; Average loss: 3.7451
Iteration: 896; Percent complete: 22.4%; Average loss: 3.6577
Iteration: 897; Percent complete: 22.4%; Average loss: 3.4572
Iteration: 898; Percent complete: 22.4%; Average loss: 3.7528
Iteration: 899; Percent complete: 22.5%; Average loss: 3.6468
Iteration: 900; Percent complete: 22.5%; Average loss: 3.3844
Iteration: 901; Percent complete: 22.5%; Average loss: 3.3078
Iteration: 902; Percent complete: 22.6%; Average loss: 3.3646
Iteration: 903; Percent complete: 22.6%; Average loss: 3.4951
Iteration: 904; Percent complete: 22.6%; Average loss: 3.3827
Iteration: 905; Percent complete: 22.6%; Average loss: 3.5205
Iteration: 906; Percent complete: 22.7%; Average loss: 3.6055
Iteration: 907; Percent complete: 22.7%; Average loss: 3.3909
Iteration: 908; Percent complete: 22.7%; Average loss: 3.3607
Iteration: 909; Percent complete: 22.7%; Average loss: 3.4456
Iteration: 910; Percent complete: 22.8%; Average loss: 3.6058
Iteration: 911; Percent complete: 22.8%; Average loss: 3.5639
Iteration: 912; Percent complete: 22.8%; Average loss: 3.5346
Iteration: 913; Percent complete: 22.8%; Average loss: 3.4029
Iteration: 914; Percent complete: 22.9%; Average loss: 3.4942
Iteration: 915; Percent complete: 22.9%; Average loss: 3.4224
Iteration: 916; Percent complete: 22.9%; Average loss: 3.4756
Iteration: 917; Percent complete: 22.9%; Average loss: 3.5174
Iteration: 918; Percent complete: 22.9%; Average loss: 3.4923
Iteration: 919; Percent complete: 23.0%; Average loss: 3.4813
Iteration: 920; Percent complete: 23.0%; Average loss: 3.3467
Iteration: 921; Percent complete: 23.0%; Average loss: 3.4134
Iteration: 922; Percent complete: 23.1%; Average loss: 3.3242
Iteration: 923; Percent complete: 23.1%; Average loss: 3.5224
Iteration: 924; Percent complete: 23.1%; Average loss: 3.4314
Iteration: 925; Percent complete: 23.1%; Average loss: 3.7101
Iteration: 926; Percent complete: 23.2%; Average loss: 3.5028
Iteration: 927; Percent complete: 23.2%; Average loss: 3.4599
Iteration: 928; Percent complete: 23.2%; Average loss: 3.5356
Iteration: 929; Percent complete: 23.2%; Average loss: 3.2455
Iteration: 930; Percent complete: 23.2%; Average loss: 3.6138
Iteration: 931; Percent complete: 23.3%; Average loss: 3.2832
Iteration: 932; Percent complete: 23.3%; Average loss: 3.5121
Iteration: 933; Percent complete: 23.3%; Average loss: 3.6625
Iteration: 934; Percent complete: 23.4%; Average loss: 3.4143
Iteration: 935; Percent complete: 23.4%; Average loss: 3.6108
Iteration: 936; Percent complete: 23.4%; Average loss: 3.3733
Iteration: 937; Percent complete: 23.4%; Average loss: 3.2121
Iteration: 938; Percent complete: 23.4%; Average loss: 3.4898
Iteration: 939; Percent complete: 23.5%; Average loss: 3.5675
Iteration: 940; Percent complete: 23.5%; Average loss: 3.3898
Iteration: 941; Percent complete: 23.5%; Average loss: 3.7779
Iteration: 942; Percent complete: 23.5%; Average loss: 3.5404
Iteration: 943; Percent complete: 23.6%; Average loss: 3.4597
Iteration: 944; Percent complete: 23.6%; Average loss: 3.4770
Iteration: 945; Percent complete: 23.6%; Average loss: 3.2131
Iteration: 946; Percent complete: 23.6%; Average loss: 3.6514
Iteration: 947; Percent complete: 23.7%; Average loss: 3.3483
Iteration: 948; Percent complete: 23.7%; Average loss: 3.5175
Iteration: 949; Percent complete: 23.7%; Average loss: 3.7068
Iteration: 950; Percent complete: 23.8%; Average loss: 3.2724
Iteration: 951; Percent complete: 23.8%; Average loss: 3.4702
Iteration: 952; Percent complete: 23.8%; Average loss: 3.2695
Iteration: 953; Percent complete: 23.8%; Average loss: 3.4904
Iteration: 954; Percent complete: 23.8%; Average loss: 3.4190
Iteration: 955; Percent complete: 23.9%; Average loss: 3.4182
Iteration: 956; Percent complete: 23.9%; Average loss: 3.4659
Iteration: 957; Percent complete: 23.9%; Average loss: 3.5376
Iteration: 958; Percent complete: 23.9%; Average loss: 3.4203
Iteration: 959; Percent complete: 24.0%; Average loss: 3.5123
Iteration: 960; Percent complete: 24.0%; Average loss: 3.4014
Iteration: 961; Percent complete: 24.0%; Average loss: 3.2762
Iteration: 962; Percent complete: 24.1%; Average loss: 3.4404
Iteration: 963; Percent complete: 24.1%; Average loss: 3.6355
Iteration: 964; Percent complete: 24.1%; Average loss: 3.4105
Iteration: 965; Percent complete: 24.1%; Average loss: 3.2638
Iteration: 966; Percent complete: 24.1%; Average loss: 3.4453
Iteration: 967; Percent complete: 24.2%; Average loss: 3.4812
Iteration: 968; Percent complete: 24.2%; Average loss: 3.2834
Iteration: 969; Percent complete: 24.2%; Average loss: 3.6066
Iteration: 970; Percent complete: 24.2%; Average loss: 3.7228
Iteration: 971; Percent complete: 24.3%; Average loss: 3.3655
Iteration: 972; Percent complete: 24.3%; Average loss: 3.3716
Iteration: 973; Percent complete: 24.3%; Average loss: 3.2982
Iteration: 974; Percent complete: 24.3%; Average loss: 3.4666
Iteration: 975; Percent complete: 24.4%; Average loss: 3.6302
Iteration: 976; Percent complete: 24.4%; Average loss: 3.3891
Iteration: 977; Percent complete: 24.4%; Average loss: 3.3980
Iteration: 978; Percent complete: 24.4%; Average loss: 3.2548
Iteration: 979; Percent complete: 24.5%; Average loss: 3.6483
Iteration: 980; Percent complete: 24.5%; Average loss: 3.5830
Iteration: 981; Percent complete: 24.5%; Average loss: 3.4783
Iteration: 982; Percent complete: 24.6%; Average loss: 3.4857
Iteration: 983; Percent complete: 24.6%; Average loss: 3.5458
Iteration: 984; Percent complete: 24.6%; Average loss: 3.2526
Iteration: 985; Percent complete: 24.6%; Average loss: 3.4130
Iteration: 986; Percent complete: 24.6%; Average loss: 3.7134
Iteration: 987; Percent complete: 24.7%; Average loss: 3.3659
Iteration: 988; Percent complete: 24.7%; Average loss: 3.5538
Iteration: 989; Percent complete: 24.7%; Average loss: 3.6931
Iteration: 990; Percent complete: 24.8%; Average loss: 3.2434
Iteration: 991; Percent complete: 24.8%; Average loss: 3.3359
Iteration: 992; Percent complete: 24.8%; Average loss: 3.5036
Iteration: 993; Percent complete: 24.8%; Average loss: 3.5176
Iteration: 994; Percent complete: 24.9%; Average loss: 3.5209
Iteration: 995; Percent complete: 24.9%; Average loss: 3.1516
Iteration: 996; Percent complete: 24.9%; Average loss: 3.3294
Iteration: 997; Percent complete: 24.9%; Average loss: 3.4293
Iteration: 998; Percent complete: 24.9%; Average loss: 3.2306
Iteration: 999; Percent complete: 25.0%; Average loss: 3.5049
Iteration: 1000; Percent complete: 25.0%; Average loss: 3.6387
Iteration: 1001; Percent complete: 25.0%; Average loss: 3.1834
Iteration: 1002; Percent complete: 25.1%; Average loss: 3.3494
Iteration: 1003; Percent complete: 25.1%; Average loss: 3.6898
Iteration: 1004; Percent complete: 25.1%; Average loss: 3.2203
Iteration: 1005; Percent complete: 25.1%; Average loss: 3.6045
Iteration: 1006; Percent complete: 25.1%; Average loss: 3.5506
Iteration: 1007; Percent complete: 25.2%; Average loss: 3.4247
Iteration: 1008; Percent complete: 25.2%; Average loss: 3.2239
Iteration: 1009; Percent complete: 25.2%; Average loss: 3.2873
Iteration: 1010; Percent complete: 25.2%; Average loss: 3.4039
Iteration: 1011; Percent complete: 25.3%; Average loss: 3.5456
Iteration: 1012; Percent complete: 25.3%; Average loss: 3.6282
Iteration: 1013; Percent complete: 25.3%; Average loss: 3.4362
Iteration: 1014; Percent complete: 25.4%; Average loss: 3.4412
Iteration: 1015; Percent complete: 25.4%; Average loss: 3.5237
Iteration: 1016; Percent complete: 25.4%; Average loss: 3.2899
Iteration: 1017; Percent complete: 25.4%; Average loss: 3.4307
Iteration: 1018; Percent complete: 25.4%; Average loss: 3.5149
Iteration: 1019; Percent complete: 25.5%; Average loss: 3.4882
Iteration: 1020; Percent complete: 25.5%; Average loss: 3.3800
Iteration: 1021; Percent complete: 25.5%; Average loss: 3.5293
Iteration: 1022; Percent complete: 25.6%; Average loss: 3.7209
Iteration: 1023; Percent complete: 25.6%; Average loss: 3.5467
Iteration: 1024; Percent complete: 25.6%; Average loss: 3.1601
Iteration: 1025; Percent complete: 25.6%; Average loss: 3.5460
Iteration: 1026; Percent complete: 25.7%; Average loss: 3.5763
Iteration: 1027; Percent complete: 25.7%; Average loss: 3.4613
Iteration: 1028; Percent complete: 25.7%; Average loss: 3.5701
Iteration: 1029; Percent complete: 25.7%; Average loss: 3.5214
Iteration: 1030; Percent complete: 25.8%; Average loss: 3.5121
Iteration: 1031; Percent complete: 25.8%; Average loss: 3.3914
Iteration: 1032; Percent complete: 25.8%; Average loss: 3.5352
Iteration: 1033; Percent complete: 25.8%; Average loss: 3.2552
Iteration: 1034; Percent complete: 25.9%; Average loss: 3.6117
Iteration: 1035; Percent complete: 25.9%; Average loss: 3.5943
Iteration: 1036; Percent complete: 25.9%; Average loss: 3.4015
Iteration: 1037; Percent complete: 25.9%; Average loss: 3.3253
Iteration: 1038; Percent complete: 25.9%; Average loss: 3.5442
Iteration: 1039; Percent complete: 26.0%; Average loss: 3.6196
Iteration: 1040; Percent complete: 26.0%; Average loss: 3.2686
Iteration: 1041; Percent complete: 26.0%; Average loss: 3.1824
Iteration: 1042; Percent complete: 26.1%; Average loss: 3.6165
Iteration: 1043; Percent complete: 26.1%; Average loss: 3.5907
Iteration: 1044; Percent complete: 26.1%; Average loss: 3.4486
Iteration: 1045; Percent complete: 26.1%; Average loss: 3.5582
Iteration: 1046; Percent complete: 26.2%; Average loss: 3.3047
Iteration: 1047; Percent complete: 26.2%; Average loss: 3.5565
Iteration: 1048; Percent complete: 26.2%; Average loss: 3.7800
Iteration: 1049; Percent complete: 26.2%; Average loss: 3.3316
Iteration: 1050; Percent complete: 26.2%; Average loss: 3.5707
Iteration: 1051; Percent complete: 26.3%; Average loss: 3.2719
Iteration: 1052; Percent complete: 26.3%; Average loss: 3.3323
Iteration: 1053; Percent complete: 26.3%; Average loss: 3.4621
Iteration: 1054; Percent complete: 26.4%; Average loss: 3.3471
Iteration: 1055; Percent complete: 26.4%; Average loss: 3.6742
Iteration: 1056; Percent complete: 26.4%; Average loss: 3.3640
Iteration: 1057; Percent complete: 26.4%; Average loss: 3.4212
Iteration: 1058; Percent complete: 26.5%; Average loss: 3.4947
Iteration: 1059; Percent complete: 26.5%; Average loss: 3.3635
Iteration: 1060; Percent complete: 26.5%; Average loss: 3.4450
Iteration: 1061; Percent complete: 26.5%; Average loss: 3.6354
Iteration: 1062; Percent complete: 26.6%; Average loss: 3.3847
Iteration: 1063; Percent complete: 26.6%; Average loss: 3.7170
Iteration: 1064; Percent complete: 26.6%; Average loss: 3.4056
Iteration: 1065; Percent complete: 26.6%; Average loss: 3.4880
Iteration: 1066; Percent complete: 26.7%; Average loss: 3.5110
Iteration: 1067; Percent complete: 26.7%; Average loss: 3.2356
Iteration: 1068; Percent complete: 26.7%; Average loss: 3.3155
Iteration: 1069; Percent complete: 26.7%; Average loss: 3.2080
Iteration: 1070; Percent complete: 26.8%; Average loss: 3.4304
Iteration: 1071; Percent complete: 26.8%; Average loss: 3.3419
Iteration: 1072; Percent complete: 26.8%; Average loss: 3.2673
Iteration: 1073; Percent complete: 26.8%; Average loss: 3.3649
Iteration: 1074; Percent complete: 26.9%; Average loss: 3.3442
Iteration: 1075; Percent complete: 26.9%; Average loss: 3.4684
Iteration: 1076; Percent complete: 26.9%; Average loss: 3.4201
Iteration: 1077; Percent complete: 26.9%; Average loss: 3.4161
Iteration: 1078; Percent complete: 27.0%; Average loss: 3.3427
Iteration: 1079; Percent complete: 27.0%; Average loss: 3.2773
Iteration: 1080; Percent complete: 27.0%; Average loss: 3.5014
Iteration: 1081; Percent complete: 27.0%; Average loss: 3.2980
Iteration: 1082; Percent complete: 27.1%; Average loss: 3.4071
Iteration: 1083; Percent complete: 27.1%; Average loss: 3.5065
Iteration: 1084; Percent complete: 27.1%; Average loss: 3.1817
Iteration: 1085; Percent complete: 27.1%; Average loss: 3.4022
Iteration: 1086; Percent complete: 27.2%; Average loss: 3.4040
Iteration: 1087; Percent complete: 27.2%; Average loss: 3.2724
Iteration: 1088; Percent complete: 27.2%; Average loss: 3.2417
Iteration: 1089; Percent complete: 27.2%; Average loss: 3.5352
Iteration: 1090; Percent complete: 27.3%; Average loss: 3.5092
Iteration: 1091; Percent complete: 27.3%; Average loss: 3.2881
Iteration: 1092; Percent complete: 27.3%; Average loss: 3.3567
Iteration: 1093; Percent complete: 27.3%; Average loss: 3.3445
Iteration: 1094; Percent complete: 27.4%; Average loss: 3.3186
Iteration: 1095; Percent complete: 27.4%; Average loss: 3.6361
Iteration: 1096; Percent complete: 27.4%; Average loss: 3.5622
Iteration: 1097; Percent complete: 27.4%; Average loss: 3.5128
Iteration: 1098; Percent complete: 27.5%; Average loss: 3.6228
Iteration: 1099; Percent complete: 27.5%; Average loss: 3.2470
Iteration: 1100; Percent complete: 27.5%; Average loss: 3.4695
Iteration: 1101; Percent complete: 27.5%; Average loss: 3.3276
Iteration: 1102; Percent complete: 27.6%; Average loss: 3.3309
Iteration: 1103; Percent complete: 27.6%; Average loss: 3.3597
Iteration: 1104; Percent complete: 27.6%; Average loss: 3.4577
Iteration: 1105; Percent complete: 27.6%; Average loss: 3.3650
Iteration: 1106; Percent complete: 27.7%; Average loss: 3.6230
Iteration: 1107; Percent complete: 27.7%; Average loss: 3.2845
Iteration: 1108; Percent complete: 27.7%; Average loss: 3.2961
Iteration: 1109; Percent complete: 27.7%; Average loss: 3.4517
Iteration: 1110; Percent complete: 27.8%; Average loss: 3.3417
Iteration: 1111; Percent complete: 27.8%; Average loss: 3.4667
Iteration: 1112; Percent complete: 27.8%; Average loss: 3.4906
Iteration: 1113; Percent complete: 27.8%; Average loss: 3.3841
Iteration: 1114; Percent complete: 27.9%; Average loss: 3.3549
Iteration: 1115; Percent complete: 27.9%; Average loss: 3.5769
Iteration: 1116; Percent complete: 27.9%; Average loss: 3.4385
Iteration: 1117; Percent complete: 27.9%; Average loss: 3.5831
Iteration: 1118; Percent complete: 28.0%; Average loss: 3.5455
Iteration: 1119; Percent complete: 28.0%; Average loss: 3.7127
Iteration: 1120; Percent complete: 28.0%; Average loss: 3.5576
Iteration: 1121; Percent complete: 28.0%; Average loss: 3.7017
Iteration: 1122; Percent complete: 28.1%; Average loss: 3.1919
Iteration: 1123; Percent complete: 28.1%; Average loss: 3.6067
Iteration: 1124; Percent complete: 28.1%; Average loss: 3.4202
Iteration: 1125; Percent complete: 28.1%; Average loss: 3.7073
Iteration: 1126; Percent complete: 28.1%; Average loss: 3.4276
Iteration: 1127; Percent complete: 28.2%; Average loss: 3.5598
Iteration: 1128; Percent complete: 28.2%; Average loss: 3.2357
Iteration: 1129; Percent complete: 28.2%; Average loss: 3.1692
Iteration: 1130; Percent complete: 28.2%; Average loss: 3.4094
Iteration: 1131; Percent complete: 28.3%; Average loss: 3.4746
Iteration: 1132; Percent complete: 28.3%; Average loss: 3.6800
Iteration: 1133; Percent complete: 28.3%; Average loss: 3.3415
Iteration: 1134; Percent complete: 28.3%; Average loss: 3.2220
Iteration: 1135; Percent complete: 28.4%; Average loss: 3.2638
Iteration: 1136; Percent complete: 28.4%; Average loss: 3.2322
Iteration: 1137; Percent complete: 28.4%; Average loss: 3.3254
Iteration: 1138; Percent complete: 28.4%; Average loss: 3.6079
Iteration: 1139; Percent complete: 28.5%; Average loss: 3.3789
Iteration: 1140; Percent complete: 28.5%; Average loss: 3.5671
Iteration: 1141; Percent complete: 28.5%; Average loss: 3.2709
Iteration: 1142; Percent complete: 28.5%; Average loss: 3.3501
Iteration: 1143; Percent complete: 28.6%; Average loss: 3.3481
Iteration: 1144; Percent complete: 28.6%; Average loss: 3.2935
Iteration: 1145; Percent complete: 28.6%; Average loss: 3.4758
Iteration: 1146; Percent complete: 28.6%; Average loss: 3.4613
Iteration: 1147; Percent complete: 28.7%; Average loss: 3.4585
Iteration: 1148; Percent complete: 28.7%; Average loss: 3.4997
Iteration: 1149; Percent complete: 28.7%; Average loss: 3.4904
Iteration: 1150; Percent complete: 28.7%; Average loss: 3.3681
Iteration: 1151; Percent complete: 28.8%; Average loss: 3.4570
Iteration: 1152; Percent complete: 28.8%; Average loss: 3.3180
Iteration: 1153; Percent complete: 28.8%; Average loss: 3.3020
Iteration: 1154; Percent complete: 28.8%; Average loss: 3.2504
Iteration: 1155; Percent complete: 28.9%; Average loss: 3.7843
Iteration: 1156; Percent complete: 28.9%; Average loss: 3.6109
Iteration: 1157; Percent complete: 28.9%; Average loss: 3.2978
Iteration: 1158; Percent complete: 28.9%; Average loss: 3.2993
Iteration: 1159; Percent complete: 29.0%; Average loss: 3.3417
Iteration: 1160; Percent complete: 29.0%; Average loss: 3.2262
Iteration: 1161; Percent complete: 29.0%; Average loss: 3.4447
Iteration: 1162; Percent complete: 29.0%; Average loss: 3.5668
Iteration: 1163; Percent complete: 29.1%; Average loss: 3.1467
Iteration: 1164; Percent complete: 29.1%; Average loss: 3.5185
Iteration: 1165; Percent complete: 29.1%; Average loss: 3.2490
Iteration: 1166; Percent complete: 29.1%; Average loss: 3.1295
Iteration: 1167; Percent complete: 29.2%; Average loss: 3.4623
Iteration: 1168; Percent complete: 29.2%; Average loss: 3.1911
Iteration: 1169; Percent complete: 29.2%; Average loss: 3.3733
Iteration: 1170; Percent complete: 29.2%; Average loss: 3.4013
Iteration: 1171; Percent complete: 29.3%; Average loss: 3.4171
Iteration: 1172; Percent complete: 29.3%; Average loss: 3.2578
Iteration: 1173; Percent complete: 29.3%; Average loss: 3.3599
Iteration: 1174; Percent complete: 29.3%; Average loss: 3.5340
Iteration: 1175; Percent complete: 29.4%; Average loss: 3.4897
Iteration: 1176; Percent complete: 29.4%; Average loss: 3.5024
Iteration: 1177; Percent complete: 29.4%; Average loss: 3.3762
Iteration: 1178; Percent complete: 29.4%; Average loss: 3.5436
Iteration: 1179; Percent complete: 29.5%; Average loss: 3.2653
Iteration: 1180; Percent complete: 29.5%; Average loss: 3.4736
Iteration: 1181; Percent complete: 29.5%; Average loss: 3.3148
Iteration: 1182; Percent complete: 29.5%; Average loss: 3.6206
Iteration: 1183; Percent complete: 29.6%; Average loss: 3.4785
Iteration: 1184; Percent complete: 29.6%; Average loss: 3.4646
Iteration: 1185; Percent complete: 29.6%; Average loss: 3.3654
Iteration: 1186; Percent complete: 29.6%; Average loss: 3.4775
Iteration: 1187; Percent complete: 29.7%; Average loss: 3.5352
Iteration: 1188; Percent complete: 29.7%; Average loss: 3.5618
Iteration: 1189; Percent complete: 29.7%; Average loss: 3.3584
Iteration: 1190; Percent complete: 29.8%; Average loss: 3.3268
Iteration: 1191; Percent complete: 29.8%; Average loss: 3.4646
Iteration: 1192; Percent complete: 29.8%; Average loss: 3.3213
Iteration: 1193; Percent complete: 29.8%; Average loss: 3.2162
Iteration: 1194; Percent complete: 29.8%; Average loss: 3.5154
Iteration: 1195; Percent complete: 29.9%; Average loss: 3.4297
Iteration: 1196; Percent complete: 29.9%; Average loss: 3.2319
Iteration: 1197; Percent complete: 29.9%; Average loss: 3.3555
Iteration: 1198; Percent complete: 29.9%; Average loss: 3.2917
Iteration: 1199; Percent complete: 30.0%; Average loss: 3.5152
Iteration: 1200; Percent complete: 30.0%; Average loss: 3.3894
Iteration: 1201; Percent complete: 30.0%; Average loss: 3.3085
Iteration: 1202; Percent complete: 30.0%; Average loss: 3.4431
Iteration: 1203; Percent complete: 30.1%; Average loss: 3.1673
Iteration: 1204; Percent complete: 30.1%; Average loss: 3.3920
Iteration: 1205; Percent complete: 30.1%; Average loss: 3.4201
Iteration: 1206; Percent complete: 30.1%; Average loss: 3.4714
Iteration: 1207; Percent complete: 30.2%; Average loss: 3.3891
Iteration: 1208; Percent complete: 30.2%; Average loss: 3.3078
Iteration: 1209; Percent complete: 30.2%; Average loss: 3.3157
Iteration: 1210; Percent complete: 30.2%; Average loss: 3.4206
Iteration: 1211; Percent complete: 30.3%; Average loss: 3.2478
Iteration: 1212; Percent complete: 30.3%; Average loss: 3.3892
Iteration: 1213; Percent complete: 30.3%; Average loss: 3.5546
Iteration: 1214; Percent complete: 30.3%; Average loss: 3.4126
Iteration: 1215; Percent complete: 30.4%; Average loss: 3.3562
Iteration: 1216; Percent complete: 30.4%; Average loss: 3.4122
Iteration: 1217; Percent complete: 30.4%; Average loss: 3.3165
Iteration: 1218; Percent complete: 30.4%; Average loss: 3.4850
Iteration: 1219; Percent complete: 30.5%; Average loss: 3.6254
Iteration: 1220; Percent complete: 30.5%; Average loss: 3.5058
Iteration: 1221; Percent complete: 30.5%; Average loss: 3.5810
Iteration: 1222; Percent complete: 30.6%; Average loss: 3.5134
Iteration: 1223; Percent complete: 30.6%; Average loss: 3.4043
Iteration: 1224; Percent complete: 30.6%; Average loss: 3.4193
Iteration: 1225; Percent complete: 30.6%; Average loss: 3.5278
Iteration: 1226; Percent complete: 30.6%; Average loss: 3.0923
Iteration: 1227; Percent complete: 30.7%; Average loss: 3.4204
Iteration: 1228; Percent complete: 30.7%; Average loss: 3.6632
Iteration: 1229; Percent complete: 30.7%; Average loss: 3.4694
Iteration: 1230; Percent complete: 30.8%; Average loss: 3.5202
Iteration: 1231; Percent complete: 30.8%; Average loss: 3.4473
Iteration: 1232; Percent complete: 30.8%; Average loss: 3.6027
Iteration: 1233; Percent complete: 30.8%; Average loss: 3.2373
Iteration: 1234; Percent complete: 30.9%; Average loss: 3.4332
Iteration: 1235; Percent complete: 30.9%; Average loss: 3.1355
Iteration: 1236; Percent complete: 30.9%; Average loss: 3.3263
Iteration: 1237; Percent complete: 30.9%; Average loss: 3.3322
Iteration: 1238; Percent complete: 30.9%; Average loss: 3.4200
Iteration: 1239; Percent complete: 31.0%; Average loss: 3.2529
Iteration: 1240; Percent complete: 31.0%; Average loss: 3.2798
Iteration: 1241; Percent complete: 31.0%; Average loss: 3.2955
Iteration: 1242; Percent complete: 31.1%; Average loss: 3.1498
Iteration: 1243; Percent complete: 31.1%; Average loss: 3.2464
Iteration: 1244; Percent complete: 31.1%; Average loss: 3.5136
Iteration: 1245; Percent complete: 31.1%; Average loss: 3.5080
Iteration: 1246; Percent complete: 31.1%; Average loss: 3.4273
Iteration: 1247; Percent complete: 31.2%; Average loss: 3.3471
Iteration: 1248; Percent complete: 31.2%; Average loss: 3.0701
Iteration: 1249; Percent complete: 31.2%; Average loss: 3.4229
Iteration: 1250; Percent complete: 31.2%; Average loss: 3.4677
Iteration: 1251; Percent complete: 31.3%; Average loss: 3.4515
Iteration: 1252; Percent complete: 31.3%; Average loss: 3.2516
Iteration: 1253; Percent complete: 31.3%; Average loss: 3.5475
Iteration: 1254; Percent complete: 31.4%; Average loss: 3.3327
Iteration: 1255; Percent complete: 31.4%; Average loss: 3.2535
Iteration: 1256; Percent complete: 31.4%; Average loss: 3.1809
Iteration: 1257; Percent complete: 31.4%; Average loss: 3.3639
Iteration: 1258; Percent complete: 31.4%; Average loss: 3.3558
Iteration: 1259; Percent complete: 31.5%; Average loss: 3.4214
Iteration: 1260; Percent complete: 31.5%; Average loss: 3.3924
Iteration: 1261; Percent complete: 31.5%; Average loss: 3.3189
Iteration: 1262; Percent complete: 31.6%; Average loss: 3.3607
Iteration: 1263; Percent complete: 31.6%; Average loss: 3.6188
Iteration: 1264; Percent complete: 31.6%; Average loss: 3.5594
Iteration: 1265; Percent complete: 31.6%; Average loss: 3.4326
Iteration: 1266; Percent complete: 31.6%; Average loss: 3.3348
Iteration: 1267; Percent complete: 31.7%; Average loss: 3.6170
Iteration: 1268; Percent complete: 31.7%; Average loss: 3.3816
Iteration: 1269; Percent complete: 31.7%; Average loss: 3.0559
Iteration: 1270; Percent complete: 31.8%; Average loss: 3.4735
Iteration: 1271; Percent complete: 31.8%; Average loss: 3.2856
Iteration: 1272; Percent complete: 31.8%; Average loss: 3.2807
Iteration: 1273; Percent complete: 31.8%; Average loss: 3.2997
Iteration: 1274; Percent complete: 31.9%; Average loss: 3.3650
Iteration: 1275; Percent complete: 31.9%; Average loss: 3.2742
Iteration: 1276; Percent complete: 31.9%; Average loss: 3.6307
Iteration: 1277; Percent complete: 31.9%; Average loss: 3.4159
Iteration: 1278; Percent complete: 31.9%; Average loss: 3.1030
Iteration: 1279; Percent complete: 32.0%; Average loss: 3.2437
Iteration: 1280; Percent complete: 32.0%; Average loss: 3.3407
Iteration: 1281; Percent complete: 32.0%; Average loss: 3.5717
Iteration: 1282; Percent complete: 32.0%; Average loss: 3.3162
Iteration: 1283; Percent complete: 32.1%; Average loss: 3.4536
Iteration: 1284; Percent complete: 32.1%; Average loss: 3.2233
Iteration: 1285; Percent complete: 32.1%; Average loss: 3.4439
Iteration: 1286; Percent complete: 32.1%; Average loss: 3.1751
Iteration: 1287; Percent complete: 32.2%; Average loss: 3.2714
Iteration: 1288; Percent complete: 32.2%; Average loss: 3.3757
Iteration: 1289; Percent complete: 32.2%; Average loss: 3.5641
Iteration: 1290; Percent complete: 32.2%; Average loss: 3.5096
Iteration: 1291; Percent complete: 32.3%; Average loss: 3.2094
Iteration: 1292; Percent complete: 32.3%; Average loss: 3.2731
Iteration: 1293; Percent complete: 32.3%; Average loss: 3.6081
Iteration: 1294; Percent complete: 32.4%; Average loss: 3.4019
Iteration: 1295; Percent complete: 32.4%; Average loss: 3.4527
Iteration: 1296; Percent complete: 32.4%; Average loss: 3.2160
Iteration: 1297; Percent complete: 32.4%; Average loss: 3.2964
Iteration: 1298; Percent complete: 32.5%; Average loss: 3.1555
Iteration: 1299; Percent complete: 32.5%; Average loss: 3.5102
Iteration: 1300; Percent complete: 32.5%; Average loss: 3.5279
Iteration: 1301; Percent complete: 32.5%; Average loss: 3.1948
Iteration: 1302; Percent complete: 32.6%; Average loss: 3.5462
Iteration: 1303; Percent complete: 32.6%; Average loss: 3.2952
Iteration: 1304; Percent complete: 32.6%; Average loss: 3.2183
Iteration: 1305; Percent complete: 32.6%; Average loss: 3.2420
Iteration: 1306; Percent complete: 32.6%; Average loss: 3.4160
Iteration: 1307; Percent complete: 32.7%; Average loss: 3.3419
Iteration: 1308; Percent complete: 32.7%; Average loss: 3.5098
Iteration: 1309; Percent complete: 32.7%; Average loss: 3.3355
Iteration: 1310; Percent complete: 32.8%; Average loss: 3.3731
Iteration: 1311; Percent complete: 32.8%; Average loss: 3.3408
Iteration: 1312; Percent complete: 32.8%; Average loss: 3.4544
Iteration: 1313; Percent complete: 32.8%; Average loss: 3.4400
Iteration: 1314; Percent complete: 32.9%; Average loss: 3.3253
Iteration: 1315; Percent complete: 32.9%; Average loss: 3.3188
Iteration: 1316; Percent complete: 32.9%; Average loss: 3.3808
Iteration: 1317; Percent complete: 32.9%; Average loss: 3.3034
Iteration: 1318; Percent complete: 33.0%; Average loss: 3.4949
Iteration: 1319; Percent complete: 33.0%; Average loss: 3.2202
Iteration: 1320; Percent complete: 33.0%; Average loss: 3.1717
Iteration: 1321; Percent complete: 33.0%; Average loss: 3.5022
Iteration: 1322; Percent complete: 33.1%; Average loss: 3.2118
Iteration: 1323; Percent complete: 33.1%; Average loss: 3.5022
Iteration: 1324; Percent complete: 33.1%; Average loss: 3.1989
Iteration: 1325; Percent complete: 33.1%; Average loss: 3.3262
Iteration: 1326; Percent complete: 33.1%; Average loss: 3.2257
Iteration: 1327; Percent complete: 33.2%; Average loss: 3.4978
Iteration: 1328; Percent complete: 33.2%; Average loss: 3.3276
Iteration: 1329; Percent complete: 33.2%; Average loss: 3.2104
Iteration: 1330; Percent complete: 33.2%; Average loss: 3.4998
Iteration: 1331; Percent complete: 33.3%; Average loss: 3.1368
Iteration: 1332; Percent complete: 33.3%; Average loss: 3.4354
Iteration: 1333; Percent complete: 33.3%; Average loss: 3.1966
Iteration: 1334; Percent complete: 33.4%; Average loss: 3.2117
Iteration: 1335; Percent complete: 33.4%; Average loss: 3.1645
Iteration: 1336; Percent complete: 33.4%; Average loss: 3.5402
Iteration: 1337; Percent complete: 33.4%; Average loss: 3.4963
Iteration: 1338; Percent complete: 33.5%; Average loss: 3.1340
Iteration: 1339; Percent complete: 33.5%; Average loss: 3.4166
Iteration: 1340; Percent complete: 33.5%; Average loss: 3.5588
Iteration: 1341; Percent complete: 33.5%; Average loss: 3.1714
Iteration: 1342; Percent complete: 33.6%; Average loss: 3.2128
Iteration: 1343; Percent complete: 33.6%; Average loss: 3.4666
Iteration: 1344; Percent complete: 33.6%; Average loss: 3.3240
Iteration: 1345; Percent complete: 33.6%; Average loss: 3.3633
Iteration: 1346; Percent complete: 33.7%; Average loss: 3.2725
Iteration: 1347; Percent complete: 33.7%; Average loss: 3.5445
Iteration: 1348; Percent complete: 33.7%; Average loss: 3.1464
Iteration: 1349; Percent complete: 33.7%; Average loss: 3.2774
Iteration: 1350; Percent complete: 33.8%; Average loss: 3.3296
Iteration: 1351; Percent complete: 33.8%; Average loss: 3.3346
Iteration: 1352; Percent complete: 33.8%; Average loss: 3.4595
Iteration: 1353; Percent complete: 33.8%; Average loss: 3.2660
Iteration: 1354; Percent complete: 33.9%; Average loss: 3.5248
Iteration: 1355; Percent complete: 33.9%; Average loss: 3.3082
Iteration: 1356; Percent complete: 33.9%; Average loss: 3.4277
Iteration: 1357; Percent complete: 33.9%; Average loss: 3.3724
Iteration: 1358; Percent complete: 34.0%; Average loss: 3.2614
Iteration: 1359; Percent complete: 34.0%; Average loss: 3.5431
Iteration: 1360; Percent complete: 34.0%; Average loss: 3.5512
Iteration: 1361; Percent complete: 34.0%; Average loss: 3.6403
Iteration: 1362; Percent complete: 34.1%; Average loss: 3.5493
Iteration: 1363; Percent complete: 34.1%; Average loss: 3.1902
Iteration: 1364; Percent complete: 34.1%; Average loss: 3.2582
Iteration: 1365; Percent complete: 34.1%; Average loss: 3.2240
Iteration: 1366; Percent complete: 34.2%; Average loss: 3.2293
Iteration: 1367; Percent complete: 34.2%; Average loss: 3.3966
Iteration: 1368; Percent complete: 34.2%; Average loss: 3.3039
Iteration: 1369; Percent complete: 34.2%; Average loss: 3.4496
Iteration: 1370; Percent complete: 34.2%; Average loss: 3.2725
Iteration: 1371; Percent complete: 34.3%; Average loss: 3.5515
Iteration: 1372; Percent complete: 34.3%; Average loss: 3.2411
Iteration: 1373; Percent complete: 34.3%; Average loss: 3.4298
Iteration: 1374; Percent complete: 34.4%; Average loss: 3.4948
Iteration: 1375; Percent complete: 34.4%; Average loss: 3.3592
Iteration: 1376; Percent complete: 34.4%; Average loss: 3.3651
Iteration: 1377; Percent complete: 34.4%; Average loss: 3.5232
Iteration: 1378; Percent complete: 34.4%; Average loss: 3.1534
Iteration: 1379; Percent complete: 34.5%; Average loss: 3.2645
Iteration: 1380; Percent complete: 34.5%; Average loss: 3.0055
Iteration: 1381; Percent complete: 34.5%; Average loss: 3.2686
Iteration: 1382; Percent complete: 34.5%; Average loss: 3.5814
Iteration: 1383; Percent complete: 34.6%; Average loss: 3.2043
Iteration: 1384; Percent complete: 34.6%; Average loss: 3.3760
Iteration: 1385; Percent complete: 34.6%; Average loss: 3.3026
Iteration: 1386; Percent complete: 34.6%; Average loss: 3.4001
Iteration: 1387; Percent complete: 34.7%; Average loss: 3.2333
Iteration: 1388; Percent complete: 34.7%; Average loss: 3.1633
Iteration: 1389; Percent complete: 34.7%; Average loss: 3.3256
Iteration: 1390; Percent complete: 34.8%; Average loss: 3.2503
Iteration: 1391; Percent complete: 34.8%; Average loss: 3.2414
Iteration: 1392; Percent complete: 34.8%; Average loss: 3.4357
Iteration: 1393; Percent complete: 34.8%; Average loss: 3.1842
Iteration: 1394; Percent complete: 34.8%; Average loss: 3.3574
Iteration: 1395; Percent complete: 34.9%; Average loss: 3.3237
Iteration: 1396; Percent complete: 34.9%; Average loss: 3.5197
Iteration: 1397; Percent complete: 34.9%; Average loss: 3.1718
Iteration: 1398; Percent complete: 34.9%; Average loss: 3.4228
Iteration: 1399; Percent complete: 35.0%; Average loss: 3.3243
Iteration: 1400; Percent complete: 35.0%; Average loss: 3.4469
Iteration: 1401; Percent complete: 35.0%; Average loss: 3.4300
Iteration: 1402; Percent complete: 35.0%; Average loss: 3.2947
Iteration: 1403; Percent complete: 35.1%; Average loss: 3.3774
Iteration: 1404; Percent complete: 35.1%; Average loss: 3.3120
Iteration: 1405; Percent complete: 35.1%; Average loss: 3.3096
Iteration: 1406; Percent complete: 35.1%; Average loss: 3.5220
Iteration: 1407; Percent complete: 35.2%; Average loss: 3.0486
Iteration: 1408; Percent complete: 35.2%; Average loss: 3.2660
Iteration: 1409; Percent complete: 35.2%; Average loss: 3.3888
Iteration: 1410; Percent complete: 35.2%; Average loss: 3.4280
Iteration: 1411; Percent complete: 35.3%; Average loss: 3.3603
Iteration: 1412; Percent complete: 35.3%; Average loss: 3.5338
Iteration: 1413; Percent complete: 35.3%; Average loss: 3.2451
Iteration: 1414; Percent complete: 35.4%; Average loss: 3.2102
Iteration: 1415; Percent complete: 35.4%; Average loss: 3.2494
Iteration: 1416; Percent complete: 35.4%; Average loss: 3.1931
Iteration: 1417; Percent complete: 35.4%; Average loss: 3.3801
Iteration: 1418; Percent complete: 35.4%; Average loss: 3.4027
Iteration: 1419; Percent complete: 35.5%; Average loss: 3.3147
Iteration: 1420; Percent complete: 35.5%; Average loss: 3.6916
Iteration: 1421; Percent complete: 35.5%; Average loss: 3.3633
Iteration: 1422; Percent complete: 35.5%; Average loss: 3.6334
Iteration: 1423; Percent complete: 35.6%; Average loss: 3.1477
Iteration: 1424; Percent complete: 35.6%; Average loss: 3.0202
Iteration: 1425; Percent complete: 35.6%; Average loss: 3.0722
Iteration: 1426; Percent complete: 35.6%; Average loss: 3.2995
Iteration: 1427; Percent complete: 35.7%; Average loss: 3.3969
Iteration: 1428; Percent complete: 35.7%; Average loss: 3.2688
Iteration: 1429; Percent complete: 35.7%; Average loss: 3.3768
Iteration: 1430; Percent complete: 35.8%; Average loss: 3.5614
Iteration: 1431; Percent complete: 35.8%; Average loss: 3.3361
Iteration: 1432; Percent complete: 35.8%; Average loss: 3.2600
Iteration: 1433; Percent complete: 35.8%; Average loss: 2.9633
Iteration: 1434; Percent complete: 35.9%; Average loss: 3.3278
Iteration: 1435; Percent complete: 35.9%; Average loss: 3.0236
Iteration: 1436; Percent complete: 35.9%; Average loss: 3.4213
Iteration: 1437; Percent complete: 35.9%; Average loss: 3.2949
Iteration: 1438; Percent complete: 35.9%; Average loss: 3.2392
Iteration: 1439; Percent complete: 36.0%; Average loss: 3.1281
Iteration: 1440; Percent complete: 36.0%; Average loss: 3.5108
Iteration: 1441; Percent complete: 36.0%; Average loss: 3.3775
Iteration: 1442; Percent complete: 36.0%; Average loss: 3.2672
Iteration: 1443; Percent complete: 36.1%; Average loss: 3.3147
Iteration: 1444; Percent complete: 36.1%; Average loss: 3.2560
Iteration: 1445; Percent complete: 36.1%; Average loss: 3.2641
Iteration: 1446; Percent complete: 36.1%; Average loss: 3.3829
Iteration: 1447; Percent complete: 36.2%; Average loss: 3.3692
Iteration: 1448; Percent complete: 36.2%; Average loss: 3.4122
Iteration: 1449; Percent complete: 36.2%; Average loss: 3.4634
Iteration: 1450; Percent complete: 36.2%; Average loss: 3.2747
Iteration: 1451; Percent complete: 36.3%; Average loss: 3.0154
Iteration: 1452; Percent complete: 36.3%; Average loss: 3.2560
Iteration: 1453; Percent complete: 36.3%; Average loss: 3.4795
Iteration: 1454; Percent complete: 36.4%; Average loss: 3.4546
Iteration: 1455; Percent complete: 36.4%; Average loss: 3.3863
Iteration: 1456; Percent complete: 36.4%; Average loss: 3.3299
Iteration: 1457; Percent complete: 36.4%; Average loss: 3.3032
Iteration: 1458; Percent complete: 36.4%; Average loss: 3.5308
Iteration: 1459; Percent complete: 36.5%; Average loss: 3.3421
Iteration: 1460; Percent complete: 36.5%; Average loss: 3.2483
Iteration: 1461; Percent complete: 36.5%; Average loss: 3.4826
Iteration: 1462; Percent complete: 36.5%; Average loss: 3.2825
Iteration: 1463; Percent complete: 36.6%; Average loss: 3.2521
Iteration: 1464; Percent complete: 36.6%; Average loss: 3.4278
Iteration: 1465; Percent complete: 36.6%; Average loss: 3.6093
Iteration: 1466; Percent complete: 36.6%; Average loss: 3.3962
Iteration: 1467; Percent complete: 36.7%; Average loss: 3.2743
Iteration: 1468; Percent complete: 36.7%; Average loss: 3.6355
Iteration: 1469; Percent complete: 36.7%; Average loss: 3.2008
Iteration: 1470; Percent complete: 36.8%; Average loss: 3.0163
Iteration: 1471; Percent complete: 36.8%; Average loss: 3.2760
Iteration: 1472; Percent complete: 36.8%; Average loss: 3.2245
Iteration: 1473; Percent complete: 36.8%; Average loss: 3.2767
Iteration: 1474; Percent complete: 36.9%; Average loss: 3.5183
Iteration: 1475; Percent complete: 36.9%; Average loss: 3.1450
Iteration: 1476; Percent complete: 36.9%; Average loss: 3.1736
Iteration: 1477; Percent complete: 36.9%; Average loss: 3.2025
Iteration: 1478; Percent complete: 37.0%; Average loss: 3.3763
Iteration: 1479; Percent complete: 37.0%; Average loss: 3.3049
Iteration: 1480; Percent complete: 37.0%; Average loss: 3.4663
Iteration: 1481; Percent complete: 37.0%; Average loss: 3.2447
Iteration: 1482; Percent complete: 37.0%; Average loss: 3.2993
Iteration: 1483; Percent complete: 37.1%; Average loss: 3.3686
Iteration: 1484; Percent complete: 37.1%; Average loss: 3.4007
Iteration: 1485; Percent complete: 37.1%; Average loss: 3.1865
Iteration: 1486; Percent complete: 37.1%; Average loss: 3.3368
Iteration: 1487; Percent complete: 37.2%; Average loss: 3.3274
Iteration: 1488; Percent complete: 37.2%; Average loss: 3.1060
Iteration: 1489; Percent complete: 37.2%; Average loss: 3.3041
Iteration: 1490; Percent complete: 37.2%; Average loss: 3.1447
Iteration: 1491; Percent complete: 37.3%; Average loss: 3.3569
Iteration: 1492; Percent complete: 37.3%; Average loss: 3.4351
Iteration: 1493; Percent complete: 37.3%; Average loss: 3.3615
Iteration: 1494; Percent complete: 37.4%; Average loss: 3.1936
Iteration: 1495; Percent complete: 37.4%; Average loss: 3.3414
Iteration: 1496; Percent complete: 37.4%; Average loss: 3.5112
Iteration: 1497; Percent complete: 37.4%; Average loss: 3.3766
Iteration: 1498; Percent complete: 37.5%; Average loss: 3.3223
Iteration: 1499; Percent complete: 37.5%; Average loss: 3.0823
Iteration: 1500; Percent complete: 37.5%; Average loss: 3.2926
Iteration: 1501; Percent complete: 37.5%; Average loss: 3.0752
Iteration: 1502; Percent complete: 37.5%; Average loss: 3.1497
Iteration: 1503; Percent complete: 37.6%; Average loss: 3.5104
Iteration: 1504; Percent complete: 37.6%; Average loss: 3.0612
Iteration: 1505; Percent complete: 37.6%; Average loss: 3.1894
Iteration: 1506; Percent complete: 37.6%; Average loss: 3.3617
Iteration: 1507; Percent complete: 37.7%; Average loss: 3.3468
Iteration: 1508; Percent complete: 37.7%; Average loss: 3.2390
Iteration: 1509; Percent complete: 37.7%; Average loss: 3.2559
Iteration: 1510; Percent complete: 37.8%; Average loss: 3.3415
Iteration: 1511; Percent complete: 37.8%; Average loss: 3.2616
Iteration: 1512; Percent complete: 37.8%; Average loss: 3.3024
Iteration: 1513; Percent complete: 37.8%; Average loss: 3.1978
Iteration: 1514; Percent complete: 37.9%; Average loss: 3.1891
Iteration: 1515; Percent complete: 37.9%; Average loss: 3.2998
Iteration: 1516; Percent complete: 37.9%; Average loss: 3.1830
Iteration: 1517; Percent complete: 37.9%; Average loss: 3.3088
Iteration: 1518; Percent complete: 38.0%; Average loss: 3.4693
Iteration: 1519; Percent complete: 38.0%; Average loss: 3.3152
Iteration: 1520; Percent complete: 38.0%; Average loss: 3.2592
Iteration: 1521; Percent complete: 38.0%; Average loss: 3.3204
Iteration: 1522; Percent complete: 38.0%; Average loss: 3.3187
Iteration: 1523; Percent complete: 38.1%; Average loss: 3.2924
Iteration: 1524; Percent complete: 38.1%; Average loss: 3.5419
Iteration: 1525; Percent complete: 38.1%; Average loss: 3.3163
Iteration: 1526; Percent complete: 38.1%; Average loss: 3.4102
Iteration: 1527; Percent complete: 38.2%; Average loss: 3.3909
Iteration: 1528; Percent complete: 38.2%; Average loss: 3.5382
Iteration: 1529; Percent complete: 38.2%; Average loss: 3.3187
Iteration: 1530; Percent complete: 38.2%; Average loss: 3.3150
Iteration: 1531; Percent complete: 38.3%; Average loss: 3.3725
Iteration: 1532; Percent complete: 38.3%; Average loss: 3.3847
Iteration: 1533; Percent complete: 38.3%; Average loss: 3.3461
Iteration: 1534; Percent complete: 38.4%; Average loss: 3.1995
Iteration: 1535; Percent complete: 38.4%; Average loss: 2.9760
Iteration: 1536; Percent complete: 38.4%; Average loss: 3.4093
Iteration: 1537; Percent complete: 38.4%; Average loss: 3.4155
Iteration: 1538; Percent complete: 38.5%; Average loss: 3.1780
Iteration: 1539; Percent complete: 38.5%; Average loss: 3.4197
Iteration: 1540; Percent complete: 38.5%; Average loss: 3.3574
Iteration: 1541; Percent complete: 38.5%; Average loss: 3.3733
Iteration: 1542; Percent complete: 38.6%; Average loss: 3.2430
Iteration: 1543; Percent complete: 38.6%; Average loss: 3.1371
Iteration: 1544; Percent complete: 38.6%; Average loss: 3.3549
Iteration: 1545; Percent complete: 38.6%; Average loss: 3.2810
Iteration: 1546; Percent complete: 38.6%; Average loss: 3.1451
Iteration: 1547; Percent complete: 38.7%; Average loss: 3.3066
Iteration: 1548; Percent complete: 38.7%; Average loss: 3.4255
Iteration: 1549; Percent complete: 38.7%; Average loss: 3.0197
Iteration: 1550; Percent complete: 38.8%; Average loss: 3.2108
Iteration: 1551; Percent complete: 38.8%; Average loss: 3.0620
Iteration: 1552; Percent complete: 38.8%; Average loss: 3.3623
Iteration: 1553; Percent complete: 38.8%; Average loss: 3.0688
Iteration: 1554; Percent complete: 38.9%; Average loss: 3.4444
Iteration: 1555; Percent complete: 38.9%; Average loss: 3.2124
Iteration: 1556; Percent complete: 38.9%; Average loss: 3.1208
Iteration: 1557; Percent complete: 38.9%; Average loss: 3.2366
Iteration: 1558; Percent complete: 39.0%; Average loss: 3.3813
Iteration: 1559; Percent complete: 39.0%; Average loss: 3.4768
Iteration: 1560; Percent complete: 39.0%; Average loss: 2.9559
Iteration: 1561; Percent complete: 39.0%; Average loss: 3.6528
Iteration: 1562; Percent complete: 39.1%; Average loss: 3.3244
Iteration: 1563; Percent complete: 39.1%; Average loss: 3.2701
Iteration: 1564; Percent complete: 39.1%; Average loss: 3.4887
Iteration: 1565; Percent complete: 39.1%; Average loss: 3.3286
Iteration: 1566; Percent complete: 39.1%; Average loss: 3.2961
Iteration: 1567; Percent complete: 39.2%; Average loss: 3.0482
Iteration: 1568; Percent complete: 39.2%; Average loss: 3.1658
Iteration: 1569; Percent complete: 39.2%; Average loss: 3.2286
Iteration: 1570; Percent complete: 39.2%; Average loss: 3.1393
Iteration: 1571; Percent complete: 39.3%; Average loss: 3.0226
Iteration: 1572; Percent complete: 39.3%; Average loss: 3.2659
Iteration: 1573; Percent complete: 39.3%; Average loss: 3.4485
Iteration: 1574; Percent complete: 39.4%; Average loss: 3.1859
Iteration: 1575; Percent complete: 39.4%; Average loss: 3.5481
Iteration: 1576; Percent complete: 39.4%; Average loss: 3.2540
Iteration: 1577; Percent complete: 39.4%; Average loss: 3.2686
Iteration: 1578; Percent complete: 39.5%; Average loss: 3.0856
Iteration: 1579; Percent complete: 39.5%; Average loss: 3.2990
Iteration: 1580; Percent complete: 39.5%; Average loss: 3.0635
Iteration: 1581; Percent complete: 39.5%; Average loss: 3.1976
Iteration: 1582; Percent complete: 39.6%; Average loss: 3.3029
Iteration: 1583; Percent complete: 39.6%; Average loss: 3.4121
Iteration: 1584; Percent complete: 39.6%; Average loss: 3.0017
Iteration: 1585; Percent complete: 39.6%; Average loss: 3.4577
Iteration: 1586; Percent complete: 39.6%; Average loss: 3.0858
Iteration: 1587; Percent complete: 39.7%; Average loss: 3.2709
Iteration: 1588; Percent complete: 39.7%; Average loss: 3.3397
Iteration: 1589; Percent complete: 39.7%; Average loss: 3.4244
Iteration: 1590; Percent complete: 39.8%; Average loss: 3.1481
Iteration: 1591; Percent complete: 39.8%; Average loss: 3.2591
Iteration: 1592; Percent complete: 39.8%; Average loss: 3.3431
Iteration: 1593; Percent complete: 39.8%; Average loss: 3.3313
Iteration: 1594; Percent complete: 39.9%; Average loss: 3.2054
Iteration: 1595; Percent complete: 39.9%; Average loss: 3.5412
Iteration: 1596; Percent complete: 39.9%; Average loss: 3.2573
Iteration: 1597; Percent complete: 39.9%; Average loss: 3.4405
Iteration: 1598; Percent complete: 40.0%; Average loss: 3.3526
Iteration: 1599; Percent complete: 40.0%; Average loss: 2.9161
Iteration: 1600; Percent complete: 40.0%; Average loss: 3.1101
Iteration: 1601; Percent complete: 40.0%; Average loss: 3.1898
Iteration: 1602; Percent complete: 40.1%; Average loss: 3.3534
Iteration: 1603; Percent complete: 40.1%; Average loss: 3.1982
Iteration: 1604; Percent complete: 40.1%; Average loss: 3.2458
Iteration: 1605; Percent complete: 40.1%; Average loss: 3.3793
Iteration: 1606; Percent complete: 40.2%; Average loss: 3.3140
Iteration: 1607; Percent complete: 40.2%; Average loss: 3.2352
Iteration: 1608; Percent complete: 40.2%; Average loss: 3.1804
Iteration: 1609; Percent complete: 40.2%; Average loss: 3.5503
Iteration: 1610; Percent complete: 40.2%; Average loss: 3.1195
Iteration: 1611; Percent complete: 40.3%; Average loss: 3.2912
Iteration: 1612; Percent complete: 40.3%; Average loss: 3.0615
Iteration: 1613; Percent complete: 40.3%; Average loss: 3.1023
Iteration: 1614; Percent complete: 40.4%; Average loss: 2.9925
Iteration: 1615; Percent complete: 40.4%; Average loss: 3.0415
Iteration: 1616; Percent complete: 40.4%; Average loss: 3.4008
Iteration: 1617; Percent complete: 40.4%; Average loss: 3.1484
Iteration: 1618; Percent complete: 40.5%; Average loss: 3.2854
Iteration: 1619; Percent complete: 40.5%; Average loss: 3.4897
Iteration: 1620; Percent complete: 40.5%; Average loss: 3.1382
Iteration: 1621; Percent complete: 40.5%; Average loss: 3.4575
Iteration: 1622; Percent complete: 40.6%; Average loss: 3.3183
Iteration: 1623; Percent complete: 40.6%; Average loss: 3.3567
Iteration: 1624; Percent complete: 40.6%; Average loss: 3.3497
Iteration: 1625; Percent complete: 40.6%; Average loss: 3.4132
Iteration: 1626; Percent complete: 40.6%; Average loss: 2.9460
Iteration: 1627; Percent complete: 40.7%; Average loss: 3.2520
Iteration: 1628; Percent complete: 40.7%; Average loss: 3.1863
Iteration: 1629; Percent complete: 40.7%; Average loss: 3.3731
Iteration: 1630; Percent complete: 40.8%; Average loss: 3.3899
Iteration: 1631; Percent complete: 40.8%; Average loss: 3.2222
Iteration: 1632; Percent complete: 40.8%; Average loss: 3.2281
Iteration: 1633; Percent complete: 40.8%; Average loss: 3.5311
Iteration: 1634; Percent complete: 40.8%; Average loss: 3.0840
Iteration: 1635; Percent complete: 40.9%; Average loss: 3.3114
Iteration: 1636; Percent complete: 40.9%; Average loss: 3.5213
Iteration: 1637; Percent complete: 40.9%; Average loss: 3.3412
Iteration: 1638; Percent complete: 40.9%; Average loss: 3.3134
Iteration: 1639; Percent complete: 41.0%; Average loss: 3.2102
Iteration: 1640; Percent complete: 41.0%; Average loss: 3.1899
Iteration: 1641; Percent complete: 41.0%; Average loss: 3.3692
Iteration: 1642; Percent complete: 41.0%; Average loss: 3.1277
Iteration: 1643; Percent complete: 41.1%; Average loss: 3.3964
Iteration: 1644; Percent complete: 41.1%; Average loss: 3.3274
Iteration: 1645; Percent complete: 41.1%; Average loss: 3.3359
Iteration: 1646; Percent complete: 41.1%; Average loss: 3.2813
Iteration: 1647; Percent complete: 41.2%; Average loss: 3.5247
Iteration: 1648; Percent complete: 41.2%; Average loss: 3.2693
Iteration: 1649; Percent complete: 41.2%; Average loss: 3.2041
Iteration: 1650; Percent complete: 41.2%; Average loss: 3.2959
Iteration: 1651; Percent complete: 41.3%; Average loss: 3.1590
Iteration: 1652; Percent complete: 41.3%; Average loss: 3.2212
Iteration: 1653; Percent complete: 41.3%; Average loss: 3.4195
Iteration: 1654; Percent complete: 41.3%; Average loss: 3.5353
Iteration: 1655; Percent complete: 41.4%; Average loss: 2.9295
Iteration: 1656; Percent complete: 41.4%; Average loss: 3.1816
Iteration: 1657; Percent complete: 41.4%; Average loss: 3.3292
Iteration: 1658; Percent complete: 41.4%; Average loss: 3.5223
Iteration: 1659; Percent complete: 41.5%; Average loss: 3.5609
Iteration: 1660; Percent complete: 41.5%; Average loss: 3.2075
Iteration: 1661; Percent complete: 41.5%; Average loss: 3.2665
Iteration: 1662; Percent complete: 41.5%; Average loss: 3.2482
Iteration: 1663; Percent complete: 41.6%; Average loss: 3.5434
Iteration: 1664; Percent complete: 41.6%; Average loss: 3.2572
Iteration: 1665; Percent complete: 41.6%; Average loss: 3.1457
Iteration: 1666; Percent complete: 41.6%; Average loss: 3.1795
Iteration: 1667; Percent complete: 41.7%; Average loss: 3.2299
Iteration: 1668; Percent complete: 41.7%; Average loss: 3.5272
Iteration: 1669; Percent complete: 41.7%; Average loss: 3.2412
Iteration: 1670; Percent complete: 41.8%; Average loss: 3.1859
Iteration: 1671; Percent complete: 41.8%; Average loss: 3.0395
Iteration: 1672; Percent complete: 41.8%; Average loss: 2.8898
Iteration: 1673; Percent complete: 41.8%; Average loss: 3.5179
Iteration: 1674; Percent complete: 41.9%; Average loss: 3.1372
Iteration: 1675; Percent complete: 41.9%; Average loss: 2.9497
Iteration: 1676; Percent complete: 41.9%; Average loss: 3.4010
Iteration: 1677; Percent complete: 41.9%; Average loss: 3.1349
Iteration: 1678; Percent complete: 41.9%; Average loss: 3.5051
Iteration: 1679; Percent complete: 42.0%; Average loss: 3.2182
Iteration: 1680; Percent complete: 42.0%; Average loss: 3.1862
Iteration: 1681; Percent complete: 42.0%; Average loss: 3.3300
Iteration: 1682; Percent complete: 42.0%; Average loss: 3.1786
Iteration: 1683; Percent complete: 42.1%; Average loss: 3.0440
Iteration: 1684; Percent complete: 42.1%; Average loss: 3.3804
Iteration: 1685; Percent complete: 42.1%; Average loss: 3.1639
Iteration: 1686; Percent complete: 42.1%; Average loss: 3.2434
Iteration: 1687; Percent complete: 42.2%; Average loss: 3.2654
Iteration: 1688; Percent complete: 42.2%; Average loss: 3.1166
Iteration: 1689; Percent complete: 42.2%; Average loss: 3.2104
Iteration: 1690; Percent complete: 42.2%; Average loss: 3.3580
Iteration: 1691; Percent complete: 42.3%; Average loss: 3.1735
Iteration: 1692; Percent complete: 42.3%; Average loss: 3.2417
Iteration: 1693; Percent complete: 42.3%; Average loss: 3.4456
Iteration: 1694; Percent complete: 42.4%; Average loss: 3.2842
Iteration: 1695; Percent complete: 42.4%; Average loss: 3.1989
Iteration: 1696; Percent complete: 42.4%; Average loss: 3.2637
Iteration: 1697; Percent complete: 42.4%; Average loss: 3.4082
Iteration: 1698; Percent complete: 42.4%; Average loss: 3.2349
Iteration: 1699; Percent complete: 42.5%; Average loss: 3.2662
Iteration: 1700; Percent complete: 42.5%; Average loss: 3.2049
Iteration: 1701; Percent complete: 42.5%; Average loss: 3.0791
Iteration: 1702; Percent complete: 42.5%; Average loss: 3.2144
Iteration: 1703; Percent complete: 42.6%; Average loss: 3.1220
Iteration: 1704; Percent complete: 42.6%; Average loss: 3.4070
Iteration: 1705; Percent complete: 42.6%; Average loss: 3.0323
Iteration: 1706; Percent complete: 42.6%; Average loss: 3.2977
Iteration: 1707; Percent complete: 42.7%; Average loss: 3.0846
Iteration: 1708; Percent complete: 42.7%; Average loss: 3.1863
Iteration: 1709; Percent complete: 42.7%; Average loss: 3.1799
Iteration: 1710; Percent complete: 42.8%; Average loss: 3.3230
Iteration: 1711; Percent complete: 42.8%; Average loss: 3.4898
Iteration: 1712; Percent complete: 42.8%; Average loss: 3.4507
Iteration: 1713; Percent complete: 42.8%; Average loss: 3.0324
Iteration: 1714; Percent complete: 42.9%; Average loss: 3.3126
Iteration: 1715; Percent complete: 42.9%; Average loss: 3.2880
Iteration: 1716; Percent complete: 42.9%; Average loss: 2.9636
Iteration: 1717; Percent complete: 42.9%; Average loss: 3.3182
Iteration: 1718; Percent complete: 43.0%; Average loss: 3.4702
Iteration: 1719; Percent complete: 43.0%; Average loss: 3.3690
Iteration: 1720; Percent complete: 43.0%; Average loss: 3.3443
Iteration: 1721; Percent complete: 43.0%; Average loss: 3.4766
Iteration: 1722; Percent complete: 43.0%; Average loss: 3.2940
Iteration: 1723; Percent complete: 43.1%; Average loss: 3.0784
Iteration: 1724; Percent complete: 43.1%; Average loss: 3.3972
Iteration: 1725; Percent complete: 43.1%; Average loss: 3.1519
Iteration: 1726; Percent complete: 43.1%; Average loss: 3.3405
Iteration: 1727; Percent complete: 43.2%; Average loss: 3.3267
Iteration: 1728; Percent complete: 43.2%; Average loss: 3.2070
Iteration: 1729; Percent complete: 43.2%; Average loss: 3.3942
Iteration: 1730; Percent complete: 43.2%; Average loss: 3.2356
Iteration: 1731; Percent complete: 43.3%; Average loss: 3.0678
Iteration: 1732; Percent complete: 43.3%; Average loss: 3.2584
Iteration: 1733; Percent complete: 43.3%; Average loss: 3.2290
Iteration: 1734; Percent complete: 43.4%; Average loss: 3.3590
Iteration: 1735; Percent complete: 43.4%; Average loss: 2.9037
Iteration: 1736; Percent complete: 43.4%; Average loss: 3.3004
Iteration: 1737; Percent complete: 43.4%; Average loss: 3.2131
Iteration: 1738; Percent complete: 43.5%; Average loss: 2.9707
Iteration: 1739; Percent complete: 43.5%; Average loss: 3.3965
Iteration: 1740; Percent complete: 43.5%; Average loss: 3.3431
Iteration: 1741; Percent complete: 43.5%; Average loss: 3.1465
Iteration: 1742; Percent complete: 43.5%; Average loss: 3.2130
Iteration: 1743; Percent complete: 43.6%; Average loss: 3.0081
Iteration: 1744; Percent complete: 43.6%; Average loss: 3.3141
Iteration: 1745; Percent complete: 43.6%; Average loss: 3.5476
Iteration: 1746; Percent complete: 43.6%; Average loss: 3.0941
Iteration: 1747; Percent complete: 43.7%; Average loss: 3.2098
Iteration: 1748; Percent complete: 43.7%; Average loss: 3.2741
Iteration: 1749; Percent complete: 43.7%; Average loss: 3.2739
Iteration: 1750; Percent complete: 43.8%; Average loss: 3.3148
Iteration: 1751; Percent complete: 43.8%; Average loss: 3.1258
Iteration: 1752; Percent complete: 43.8%; Average loss: 3.2086
Iteration: 1753; Percent complete: 43.8%; Average loss: 3.2312
Iteration: 1754; Percent complete: 43.9%; Average loss: 3.0910
Iteration: 1755; Percent complete: 43.9%; Average loss: 3.1273
Iteration: 1756; Percent complete: 43.9%; Average loss: 3.2314
Iteration: 1757; Percent complete: 43.9%; Average loss: 3.2347
Iteration: 1758; Percent complete: 44.0%; Average loss: 3.1301
Iteration: 1759; Percent complete: 44.0%; Average loss: 3.2848
Iteration: 1760; Percent complete: 44.0%; Average loss: 3.2875
Iteration: 1761; Percent complete: 44.0%; Average loss: 3.1033
Iteration: 1762; Percent complete: 44.0%; Average loss: 3.1135
Iteration: 1763; Percent complete: 44.1%; Average loss: 3.4018
Iteration: 1764; Percent complete: 44.1%; Average loss: 3.0539
Iteration: 1765; Percent complete: 44.1%; Average loss: 3.1795
Iteration: 1766; Percent complete: 44.1%; Average loss: 3.1819
Iteration: 1767; Percent complete: 44.2%; Average loss: 3.1558
Iteration: 1768; Percent complete: 44.2%; Average loss: 3.3845
Iteration: 1769; Percent complete: 44.2%; Average loss: 3.4704
Iteration: 1770; Percent complete: 44.2%; Average loss: 2.9424
Iteration: 1771; Percent complete: 44.3%; Average loss: 3.2112
Iteration: 1772; Percent complete: 44.3%; Average loss: 3.3592
Iteration: 1773; Percent complete: 44.3%; Average loss: 2.9543
Iteration: 1774; Percent complete: 44.4%; Average loss: 3.0701
Iteration: 1775; Percent complete: 44.4%; Average loss: 3.0800
Iteration: 1776; Percent complete: 44.4%; Average loss: 3.2833
Iteration: 1777; Percent complete: 44.4%; Average loss: 3.1472
Iteration: 1778; Percent complete: 44.5%; Average loss: 3.2839
Iteration: 1779; Percent complete: 44.5%; Average loss: 3.2495
Iteration: 1780; Percent complete: 44.5%; Average loss: 3.2565
Iteration: 1781; Percent complete: 44.5%; Average loss: 3.1706
Iteration: 1782; Percent complete: 44.5%; Average loss: 3.0180
Iteration: 1783; Percent complete: 44.6%; Average loss: 3.0823
Iteration: 1784; Percent complete: 44.6%; Average loss: 3.2956
Iteration: 1785; Percent complete: 44.6%; Average loss: 3.2177
Iteration: 1786; Percent complete: 44.6%; Average loss: 3.0428
Iteration: 1787; Percent complete: 44.7%; Average loss: 3.1996
Iteration: 1788; Percent complete: 44.7%; Average loss: 3.4823
Iteration: 1789; Percent complete: 44.7%; Average loss: 3.0724
Iteration: 1790; Percent complete: 44.8%; Average loss: 3.2440
Iteration: 1791; Percent complete: 44.8%; Average loss: 3.3914
Iteration: 1792; Percent complete: 44.8%; Average loss: 3.2210
Iteration: 1793; Percent complete: 44.8%; Average loss: 3.2801
Iteration: 1794; Percent complete: 44.9%; Average loss: 3.2590
Iteration: 1795; Percent complete: 44.9%; Average loss: 3.0524
Iteration: 1796; Percent complete: 44.9%; Average loss: 3.2375
Iteration: 1797; Percent complete: 44.9%; Average loss: 3.1936
Iteration: 1798; Percent complete: 45.0%; Average loss: 3.0389
Iteration: 1799; Percent complete: 45.0%; Average loss: 2.8344
Iteration: 1800; Percent complete: 45.0%; Average loss: 3.3621
Iteration: 1801; Percent complete: 45.0%; Average loss: 3.2494
Iteration: 1802; Percent complete: 45.1%; Average loss: 3.1905
Iteration: 1803; Percent complete: 45.1%; Average loss: 3.0799
Iteration: 1804; Percent complete: 45.1%; Average loss: 3.3151
Iteration: 1805; Percent complete: 45.1%; Average loss: 3.3339
Iteration: 1806; Percent complete: 45.1%; Average loss: 3.0715
Iteration: 1807; Percent complete: 45.2%; Average loss: 3.5780
Iteration: 1808; Percent complete: 45.2%; Average loss: 2.9671
Iteration: 1809; Percent complete: 45.2%; Average loss: 3.2179
Iteration: 1810; Percent complete: 45.2%; Average loss: 3.1662
Iteration: 1811; Percent complete: 45.3%; Average loss: 3.0826
Iteration: 1812; Percent complete: 45.3%; Average loss: 2.9593
Iteration: 1813; Percent complete: 45.3%; Average loss: 3.0304
Iteration: 1814; Percent complete: 45.4%; Average loss: 3.2954
Iteration: 1815; Percent complete: 45.4%; Average loss: 3.4758
Iteration: 1816; Percent complete: 45.4%; Average loss: 3.0209
Iteration: 1817; Percent complete: 45.4%; Average loss: 3.1794
Iteration: 1818; Percent complete: 45.5%; Average loss: 3.1049
Iteration: 1819; Percent complete: 45.5%; Average loss: 3.0555
Iteration: 1820; Percent complete: 45.5%; Average loss: 3.3290
Iteration: 1821; Percent complete: 45.5%; Average loss: 3.2030
Iteration: 1822; Percent complete: 45.6%; Average loss: 3.1189
Iteration: 1823; Percent complete: 45.6%; Average loss: 2.9595
Iteration: 1824; Percent complete: 45.6%; Average loss: 3.4061
Iteration: 1825; Percent complete: 45.6%; Average loss: 3.1822
Iteration: 1826; Percent complete: 45.6%; Average loss: 3.0387
Iteration: 1827; Percent complete: 45.7%; Average loss: 3.2958
Iteration: 1828; Percent complete: 45.7%; Average loss: 3.2009
Iteration: 1829; Percent complete: 45.7%; Average loss: 2.9460
Iteration: 1830; Percent complete: 45.8%; Average loss: 3.2716
Iteration: 1831; Percent complete: 45.8%; Average loss: 3.1371
Iteration: 1832; Percent complete: 45.8%; Average loss: 3.3361
Iteration: 1833; Percent complete: 45.8%; Average loss: 2.9976
Iteration: 1834; Percent complete: 45.9%; Average loss: 3.2388
Iteration: 1835; Percent complete: 45.9%; Average loss: 3.2804
Iteration: 1836; Percent complete: 45.9%; Average loss: 3.1088
Iteration: 1837; Percent complete: 45.9%; Average loss: 3.1241
Iteration: 1838; Percent complete: 46.0%; Average loss: 3.3470
Iteration: 1839; Percent complete: 46.0%; Average loss: 3.2113
Iteration: 1840; Percent complete: 46.0%; Average loss: 3.4969
Iteration: 1841; Percent complete: 46.0%; Average loss: 3.3969
Iteration: 1842; Percent complete: 46.1%; Average loss: 3.4338
Iteration: 1843; Percent complete: 46.1%; Average loss: 3.3065
Iteration: 1844; Percent complete: 46.1%; Average loss: 3.3107
Iteration: 1845; Percent complete: 46.1%; Average loss: 3.1160
Iteration: 1846; Percent complete: 46.2%; Average loss: 2.9637
Iteration: 1847; Percent complete: 46.2%; Average loss: 3.2659
Iteration: 1848; Percent complete: 46.2%; Average loss: 2.9947
Iteration: 1849; Percent complete: 46.2%; Average loss: 3.0844
Iteration: 1850; Percent complete: 46.2%; Average loss: 3.2718
Iteration: 1851; Percent complete: 46.3%; Average loss: 3.3186
Iteration: 1852; Percent complete: 46.3%; Average loss: 3.1501
Iteration: 1853; Percent complete: 46.3%; Average loss: 3.0647
Iteration: 1854; Percent complete: 46.4%; Average loss: 3.0948
Iteration: 1855; Percent complete: 46.4%; Average loss: 3.4209
Iteration: 1856; Percent complete: 46.4%; Average loss: 3.1897
Iteration: 1857; Percent complete: 46.4%; Average loss: 3.2008
Iteration: 1858; Percent complete: 46.5%; Average loss: 3.1977
Iteration: 1859; Percent complete: 46.5%; Average loss: 3.2897
Iteration: 1860; Percent complete: 46.5%; Average loss: 3.2065
Iteration: 1861; Percent complete: 46.5%; Average loss: 3.0001
Iteration: 1862; Percent complete: 46.6%; Average loss: 3.1619
Iteration: 1863; Percent complete: 46.6%; Average loss: 3.1100
Iteration: 1864; Percent complete: 46.6%; Average loss: 3.3255
Iteration: 1865; Percent complete: 46.6%; Average loss: 3.0933
Iteration: 1866; Percent complete: 46.7%; Average loss: 3.2137
Iteration: 1867; Percent complete: 46.7%; Average loss: 3.0476
Iteration: 1868; Percent complete: 46.7%; Average loss: 3.1885
Iteration: 1869; Percent complete: 46.7%; Average loss: 3.3539
Iteration: 1870; Percent complete: 46.8%; Average loss: 3.1534
Iteration: 1871; Percent complete: 46.8%; Average loss: 3.0549
Iteration: 1872; Percent complete: 46.8%; Average loss: 3.4745
Iteration: 1873; Percent complete: 46.8%; Average loss: 3.1982
Iteration: 1874; Percent complete: 46.9%; Average loss: 3.1865
Iteration: 1875; Percent complete: 46.9%; Average loss: 3.0821
Iteration: 1876; Percent complete: 46.9%; Average loss: 3.0325
Iteration: 1877; Percent complete: 46.9%; Average loss: 3.1551
Iteration: 1878; Percent complete: 46.9%; Average loss: 3.3386
Iteration: 1879; Percent complete: 47.0%; Average loss: 3.1301
Iteration: 1880; Percent complete: 47.0%; Average loss: 3.1544
Iteration: 1881; Percent complete: 47.0%; Average loss: 3.1592
Iteration: 1882; Percent complete: 47.0%; Average loss: 3.3610
Iteration: 1883; Percent complete: 47.1%; Average loss: 2.9657
Iteration: 1884; Percent complete: 47.1%; Average loss: 3.0473
Iteration: 1885; Percent complete: 47.1%; Average loss: 3.1443
Iteration: 1886; Percent complete: 47.1%; Average loss: 3.1272
Iteration: 1887; Percent complete: 47.2%; Average loss: 2.9122
Iteration: 1888; Percent complete: 47.2%; Average loss: 3.2478
Iteration: 1889; Percent complete: 47.2%; Average loss: 3.3735
Iteration: 1890; Percent complete: 47.2%; Average loss: 3.4388
Iteration: 1891; Percent complete: 47.3%; Average loss: 3.1898
Iteration: 1892; Percent complete: 47.3%; Average loss: 3.1076
Iteration: 1893; Percent complete: 47.3%; Average loss: 3.3526
Iteration: 1894; Percent complete: 47.3%; Average loss: 3.3305
Iteration: 1895; Percent complete: 47.4%; Average loss: 3.1717
Iteration: 1896; Percent complete: 47.4%; Average loss: 3.2282
Iteration: 1897; Percent complete: 47.4%; Average loss: 3.3156
Iteration: 1898; Percent complete: 47.4%; Average loss: 3.1989
Iteration: 1899; Percent complete: 47.5%; Average loss: 3.3152
Iteration: 1900; Percent complete: 47.5%; Average loss: 3.1872
Iteration: 1901; Percent complete: 47.5%; Average loss: 3.3060
Iteration: 1902; Percent complete: 47.5%; Average loss: 2.9969
Iteration: 1903; Percent complete: 47.6%; Average loss: 3.2324
Iteration: 1904; Percent complete: 47.6%; Average loss: 3.0432
Iteration: 1905; Percent complete: 47.6%; Average loss: 3.0689
Iteration: 1906; Percent complete: 47.6%; Average loss: 3.1358
Iteration: 1907; Percent complete: 47.7%; Average loss: 3.3332
Iteration: 1908; Percent complete: 47.7%; Average loss: 3.3300
Iteration: 1909; Percent complete: 47.7%; Average loss: 2.9927
Iteration: 1910; Percent complete: 47.8%; Average loss: 3.0372
Iteration: 1911; Percent complete: 47.8%; Average loss: 3.3692
Iteration: 1912; Percent complete: 47.8%; Average loss: 3.0803
Iteration: 1913; Percent complete: 47.8%; Average loss: 3.2164
Iteration: 1914; Percent complete: 47.9%; Average loss: 3.1889
Iteration: 1915; Percent complete: 47.9%; Average loss: 3.0030
Iteration: 1916; Percent complete: 47.9%; Average loss: 3.0893
Iteration: 1917; Percent complete: 47.9%; Average loss: 2.9163
Iteration: 1918; Percent complete: 47.9%; Average loss: 3.2378
Iteration: 1919; Percent complete: 48.0%; Average loss: 3.1695
Iteration: 1920; Percent complete: 48.0%; Average loss: 3.1100
Iteration: 1921; Percent complete: 48.0%; Average loss: 3.0396
Iteration: 1922; Percent complete: 48.0%; Average loss: 3.2274
Iteration: 1923; Percent complete: 48.1%; Average loss: 3.2848
Iteration: 1924; Percent complete: 48.1%; Average loss: 3.1593
Iteration: 1925; Percent complete: 48.1%; Average loss: 3.1546
Iteration: 1926; Percent complete: 48.1%; Average loss: 3.1511
Iteration: 1927; Percent complete: 48.2%; Average loss: 3.0504
Iteration: 1928; Percent complete: 48.2%; Average loss: 3.1688
Iteration: 1929; Percent complete: 48.2%; Average loss: 3.1331
Iteration: 1930; Percent complete: 48.2%; Average loss: 2.8913
Iteration: 1931; Percent complete: 48.3%; Average loss: 3.2352
Iteration: 1932; Percent complete: 48.3%; Average loss: 3.0166
Iteration: 1933; Percent complete: 48.3%; Average loss: 3.3071
Iteration: 1934; Percent complete: 48.4%; Average loss: 3.1024
Iteration: 1935; Percent complete: 48.4%; Average loss: 3.3004
Iteration: 1936; Percent complete: 48.4%; Average loss: 3.1355
Iteration: 1937; Percent complete: 48.4%; Average loss: 3.0512
Iteration: 1938; Percent complete: 48.4%; Average loss: 3.2763
Iteration: 1939; Percent complete: 48.5%; Average loss: 3.0554
Iteration: 1940; Percent complete: 48.5%; Average loss: 3.2103
Iteration: 1941; Percent complete: 48.5%; Average loss: 3.0530
Iteration: 1942; Percent complete: 48.5%; Average loss: 3.2550
Iteration: 1943; Percent complete: 48.6%; Average loss: 3.1360
Iteration: 1944; Percent complete: 48.6%; Average loss: 2.9908
Iteration: 1945; Percent complete: 48.6%; Average loss: 3.1422
Iteration: 1946; Percent complete: 48.6%; Average loss: 3.3050
Iteration: 1947; Percent complete: 48.7%; Average loss: 3.2231
Iteration: 1948; Percent complete: 48.7%; Average loss: 3.1694
Iteration: 1949; Percent complete: 48.7%; Average loss: 3.3265
Iteration: 1950; Percent complete: 48.8%; Average loss: 3.2561
Iteration: 1951; Percent complete: 48.8%; Average loss: 3.0156
Iteration: 1952; Percent complete: 48.8%; Average loss: 3.2502
Iteration: 1953; Percent complete: 48.8%; Average loss: 3.1242
Iteration: 1954; Percent complete: 48.9%; Average loss: 3.0776
Iteration: 1955; Percent complete: 48.9%; Average loss: 2.9028
Iteration: 1956; Percent complete: 48.9%; Average loss: 3.1181
Iteration: 1957; Percent complete: 48.9%; Average loss: 2.9267
Iteration: 1958; Percent complete: 48.9%; Average loss: 3.3861
Iteration: 1959; Percent complete: 49.0%; Average loss: 3.2271
Iteration: 1960; Percent complete: 49.0%; Average loss: 3.3744
Iteration: 1961; Percent complete: 49.0%; Average loss: 2.8958
Iteration: 1962; Percent complete: 49.0%; Average loss: 3.1574
Iteration: 1963; Percent complete: 49.1%; Average loss: 3.3019
Iteration: 1964; Percent complete: 49.1%; Average loss: 3.0279
Iteration: 1965; Percent complete: 49.1%; Average loss: 3.0946
Iteration: 1966; Percent complete: 49.1%; Average loss: 2.9150
Iteration: 1967; Percent complete: 49.2%; Average loss: 3.2326
Iteration: 1968; Percent complete: 49.2%; Average loss: 2.6713
Iteration: 1969; Percent complete: 49.2%; Average loss: 2.7983
Iteration: 1970; Percent complete: 49.2%; Average loss: 3.0975
Iteration: 1971; Percent complete: 49.3%; Average loss: 3.2136
Iteration: 1972; Percent complete: 49.3%; Average loss: 2.8199
Iteration: 1973; Percent complete: 49.3%; Average loss: 2.9988
Iteration: 1974; Percent complete: 49.4%; Average loss: 3.3098
Iteration: 1975; Percent complete: 49.4%; Average loss: 2.8068
Iteration: 1976; Percent complete: 49.4%; Average loss: 3.3087
Iteration: 1977; Percent complete: 49.4%; Average loss: 2.9995
Iteration: 1978; Percent complete: 49.5%; Average loss: 2.9864
Iteration: 1979; Percent complete: 49.5%; Average loss: 3.1514
Iteration: 1980; Percent complete: 49.5%; Average loss: 3.1583
Iteration: 1981; Percent complete: 49.5%; Average loss: 3.3179
Iteration: 1982; Percent complete: 49.5%; Average loss: 3.1712
Iteration: 1983; Percent complete: 49.6%; Average loss: 3.3341
Iteration: 1984; Percent complete: 49.6%; Average loss: 3.0698
Iteration: 1985; Percent complete: 49.6%; Average loss: 3.2002
Iteration: 1986; Percent complete: 49.6%; Average loss: 3.3794
Iteration: 1987; Percent complete: 49.7%; Average loss: 3.0442
Iteration: 1988; Percent complete: 49.7%; Average loss: 3.3650
Iteration: 1989; Percent complete: 49.7%; Average loss: 3.1290
Iteration: 1990; Percent complete: 49.8%; Average loss: 3.1087
Iteration: 1991; Percent complete: 49.8%; Average loss: 3.2650
Iteration: 1992; Percent complete: 49.8%; Average loss: 3.0630
Iteration: 1993; Percent complete: 49.8%; Average loss: 3.3359
Iteration: 1994; Percent complete: 49.9%; Average loss: 3.3008
Iteration: 1995; Percent complete: 49.9%; Average loss: 3.1250
Iteration: 1996; Percent complete: 49.9%; Average loss: 2.9477
Iteration: 1997; Percent complete: 49.9%; Average loss: 3.2557
Iteration: 1998; Percent complete: 50.0%; Average loss: 2.9821
Iteration: 1999; Percent complete: 50.0%; Average loss: 2.9346
Iteration: 2000; Percent complete: 50.0%; Average loss: 3.1813
Iteration: 2001; Percent complete: 50.0%; Average loss: 3.1475
Iteration: 2002; Percent complete: 50.0%; Average loss: 3.2343
Iteration: 2003; Percent complete: 50.1%; Average loss: 3.1121
Iteration: 2004; Percent complete: 50.1%; Average loss: 3.1441
Iteration: 2005; Percent complete: 50.1%; Average loss: 2.8602
Iteration: 2006; Percent complete: 50.1%; Average loss: 2.9809
Iteration: 2007; Percent complete: 50.2%; Average loss: 3.1863
Iteration: 2008; Percent complete: 50.2%; Average loss: 3.2618
Iteration: 2009; Percent complete: 50.2%; Average loss: 3.0975
Iteration: 2010; Percent complete: 50.2%; Average loss: 2.8648
Iteration: 2011; Percent complete: 50.3%; Average loss: 2.9709
Iteration: 2012; Percent complete: 50.3%; Average loss: 3.2975
Iteration: 2013; Percent complete: 50.3%; Average loss: 3.0317
Iteration: 2014; Percent complete: 50.3%; Average loss: 3.1547
Iteration: 2015; Percent complete: 50.4%; Average loss: 3.0395
Iteration: 2016; Percent complete: 50.4%; Average loss: 3.2104
Iteration: 2017; Percent complete: 50.4%; Average loss: 3.2869
Iteration: 2018; Percent complete: 50.4%; Average loss: 3.0310
Iteration: 2019; Percent complete: 50.5%; Average loss: 3.2656
Iteration: 2020; Percent complete: 50.5%; Average loss: 3.0645
Iteration: 2021; Percent complete: 50.5%; Average loss: 3.1543
Iteration: 2022; Percent complete: 50.5%; Average loss: 3.1652
Iteration: 2023; Percent complete: 50.6%; Average loss: 3.0937
Iteration: 2024; Percent complete: 50.6%; Average loss: 3.2748
Iteration: 2025; Percent complete: 50.6%; Average loss: 2.9852
Iteration: 2026; Percent complete: 50.6%; Average loss: 3.2910
Iteration: 2027; Percent complete: 50.7%; Average loss: 2.9202
Iteration: 2028; Percent complete: 50.7%; Average loss: 3.2265
Iteration: 2029; Percent complete: 50.7%; Average loss: 3.3703
Iteration: 2030; Percent complete: 50.7%; Average loss: 3.5504
Iteration: 2031; Percent complete: 50.8%; Average loss: 3.0551
Iteration: 2032; Percent complete: 50.8%; Average loss: 3.4202
Iteration: 2033; Percent complete: 50.8%; Average loss: 3.1914
Iteration: 2034; Percent complete: 50.8%; Average loss: 2.9370
Iteration: 2035; Percent complete: 50.9%; Average loss: 3.2164
Iteration: 2036; Percent complete: 50.9%; Average loss: 3.3444
Iteration: 2037; Percent complete: 50.9%; Average loss: 3.1733
Iteration: 2038; Percent complete: 50.9%; Average loss: 3.8169
Iteration: 2039; Percent complete: 51.0%; Average loss: 3.0858
Iteration: 2040; Percent complete: 51.0%; Average loss: 3.2333
Iteration: 2041; Percent complete: 51.0%; Average loss: 2.9921
Iteration: 2042; Percent complete: 51.0%; Average loss: 3.2858
Iteration: 2043; Percent complete: 51.1%; Average loss: 3.2972
Iteration: 2044; Percent complete: 51.1%; Average loss: 3.1635
Iteration: 2045; Percent complete: 51.1%; Average loss: 3.1324
Iteration: 2046; Percent complete: 51.1%; Average loss: 3.3338
Iteration: 2047; Percent complete: 51.2%; Average loss: 3.1319
Iteration: 2048; Percent complete: 51.2%; Average loss: 3.0370
Iteration: 2049; Percent complete: 51.2%; Average loss: 3.1743
Iteration: 2050; Percent complete: 51.2%; Average loss: 3.6472
Iteration: 2051; Percent complete: 51.3%; Average loss: 3.1968
Iteration: 2052; Percent complete: 51.3%; Average loss: 2.8309
Iteration: 2053; Percent complete: 51.3%; Average loss: 3.1774
Iteration: 2054; Percent complete: 51.3%; Average loss: 3.2557
Iteration: 2055; Percent complete: 51.4%; Average loss: 3.1757
Iteration: 2056; Percent complete: 51.4%; Average loss: 3.2700
Iteration: 2057; Percent complete: 51.4%; Average loss: 2.8235
Iteration: 2058; Percent complete: 51.4%; Average loss: 3.0344
Iteration: 2059; Percent complete: 51.5%; Average loss: 3.2823
Iteration: 2060; Percent complete: 51.5%; Average loss: 3.1004
Iteration: 2061; Percent complete: 51.5%; Average loss: 3.1516
Iteration: 2062; Percent complete: 51.5%; Average loss: 3.0340
Iteration: 2063; Percent complete: 51.6%; Average loss: 3.2997
Iteration: 2064; Percent complete: 51.6%; Average loss: 3.0677
Iteration: 2065; Percent complete: 51.6%; Average loss: 3.0617
Iteration: 2066; Percent complete: 51.6%; Average loss: 3.1099
Iteration: 2067; Percent complete: 51.7%; Average loss: 3.2164
Iteration: 2068; Percent complete: 51.7%; Average loss: 3.4755
Iteration: 2069; Percent complete: 51.7%; Average loss: 3.0304
Iteration: 2070; Percent complete: 51.7%; Average loss: 3.0600
Iteration: 2071; Percent complete: 51.8%; Average loss: 3.1038
Iteration: 2072; Percent complete: 51.8%; Average loss: 3.2130
Iteration: 2073; Percent complete: 51.8%; Average loss: 3.0369
Iteration: 2074; Percent complete: 51.8%; Average loss: 3.3695
Iteration: 2075; Percent complete: 51.9%; Average loss: 3.4212
Iteration: 2076; Percent complete: 51.9%; Average loss: 3.1886
Iteration: 2077; Percent complete: 51.9%; Average loss: 3.1430
Iteration: 2078; Percent complete: 51.9%; Average loss: 3.2065
Iteration: 2079; Percent complete: 52.0%; Average loss: 3.0040
Iteration: 2080; Percent complete: 52.0%; Average loss: 3.4803
Iteration: 2081; Percent complete: 52.0%; Average loss: 3.2463
Iteration: 2082; Percent complete: 52.0%; Average loss: 3.0446
Iteration: 2083; Percent complete: 52.1%; Average loss: 3.1476
Iteration: 2084; Percent complete: 52.1%; Average loss: 3.0866
Iteration: 2085; Percent complete: 52.1%; Average loss: 3.1609
Iteration: 2086; Percent complete: 52.1%; Average loss: 3.0339
Iteration: 2087; Percent complete: 52.2%; Average loss: 3.1609
Iteration: 2088; Percent complete: 52.2%; Average loss: 3.0276
Iteration: 2089; Percent complete: 52.2%; Average loss: 2.9975
Iteration: 2090; Percent complete: 52.2%; Average loss: 3.0599
Iteration: 2091; Percent complete: 52.3%; Average loss: 3.1130
Iteration: 2092; Percent complete: 52.3%; Average loss: 3.3770
Iteration: 2093; Percent complete: 52.3%; Average loss: 3.0876
Iteration: 2094; Percent complete: 52.3%; Average loss: 3.0386
Iteration: 2095; Percent complete: 52.4%; Average loss: 3.1395
Iteration: 2096; Percent complete: 52.4%; Average loss: 3.2155
Iteration: 2097; Percent complete: 52.4%; Average loss: 3.0455
Iteration: 2098; Percent complete: 52.4%; Average loss: 3.1432
Iteration: 2099; Percent complete: 52.5%; Average loss: 3.2066
Iteration: 2100; Percent complete: 52.5%; Average loss: 3.1299
Iteration: 2101; Percent complete: 52.5%; Average loss: 3.1169
Iteration: 2102; Percent complete: 52.5%; Average loss: 3.3719
Iteration: 2103; Percent complete: 52.6%; Average loss: 3.0875
Iteration: 2104; Percent complete: 52.6%; Average loss: 3.0900
Iteration: 2105; Percent complete: 52.6%; Average loss: 3.1238
Iteration: 2106; Percent complete: 52.6%; Average loss: 2.9290
Iteration: 2107; Percent complete: 52.7%; Average loss: 3.1894
Iteration: 2108; Percent complete: 52.7%; Average loss: 3.1093
Iteration: 2109; Percent complete: 52.7%; Average loss: 3.2037
Iteration: 2110; Percent complete: 52.8%; Average loss: 3.1924
Iteration: 2111; Percent complete: 52.8%; Average loss: 3.0342
Iteration: 2112; Percent complete: 52.8%; Average loss: 3.1341
Iteration: 2113; Percent complete: 52.8%; Average loss: 2.8243
Iteration: 2114; Percent complete: 52.8%; Average loss: 3.1220
Iteration: 2115; Percent complete: 52.9%; Average loss: 3.3688
Iteration: 2116; Percent complete: 52.9%; Average loss: 3.0083
Iteration: 2117; Percent complete: 52.9%; Average loss: 3.0820
Iteration: 2118; Percent complete: 52.9%; Average loss: 3.0383
Iteration: 2119; Percent complete: 53.0%; Average loss: 3.2956
Iteration: 2120; Percent complete: 53.0%; Average loss: 2.9442
Iteration: 2121; Percent complete: 53.0%; Average loss: 3.1099
Iteration: 2122; Percent complete: 53.0%; Average loss: 3.0593
Iteration: 2123; Percent complete: 53.1%; Average loss: 3.1823
Iteration: 2124; Percent complete: 53.1%; Average loss: 3.0421
Iteration: 2125; Percent complete: 53.1%; Average loss: 3.1470
Iteration: 2126; Percent complete: 53.1%; Average loss: 3.1309
Iteration: 2127; Percent complete: 53.2%; Average loss: 3.1036
Iteration: 2128; Percent complete: 53.2%; Average loss: 2.9611
Iteration: 2129; Percent complete: 53.2%; Average loss: 3.0652
Iteration: 2130; Percent complete: 53.2%; Average loss: 3.2040
Iteration: 2131; Percent complete: 53.3%; Average loss: 3.1567
Iteration: 2132; Percent complete: 53.3%; Average loss: 3.1334
Iteration: 2133; Percent complete: 53.3%; Average loss: 3.3188
Iteration: 2134; Percent complete: 53.3%; Average loss: 3.0605
Iteration: 2135; Percent complete: 53.4%; Average loss: 3.1177
Iteration: 2136; Percent complete: 53.4%; Average loss: 2.8930
Iteration: 2137; Percent complete: 53.4%; Average loss: 2.9453
Iteration: 2138; Percent complete: 53.4%; Average loss: 3.0177
Iteration: 2139; Percent complete: 53.5%; Average loss: 3.0614
Iteration: 2140; Percent complete: 53.5%; Average loss: 2.9399
Iteration: 2141; Percent complete: 53.5%; Average loss: 3.2739
Iteration: 2142; Percent complete: 53.5%; Average loss: 3.1069
Iteration: 2143; Percent complete: 53.6%; Average loss: 3.3438
Iteration: 2144; Percent complete: 53.6%; Average loss: 2.9856
Iteration: 2145; Percent complete: 53.6%; Average loss: 3.0009
Iteration: 2146; Percent complete: 53.6%; Average loss: 3.0645
Iteration: 2147; Percent complete: 53.7%; Average loss: 3.2624
Iteration: 2148; Percent complete: 53.7%; Average loss: 3.3300
Iteration: 2149; Percent complete: 53.7%; Average loss: 3.2074
Iteration: 2150; Percent complete: 53.8%; Average loss: 2.7445
Iteration: 2151; Percent complete: 53.8%; Average loss: 3.0694
Iteration: 2152; Percent complete: 53.8%; Average loss: 2.9826
Iteration: 2153; Percent complete: 53.8%; Average loss: 3.0965
Iteration: 2154; Percent complete: 53.8%; Average loss: 2.8599
Iteration: 2155; Percent complete: 53.9%; Average loss: 3.2938
Iteration: 2156; Percent complete: 53.9%; Average loss: 3.1980
Iteration: 2157; Percent complete: 53.9%; Average loss: 3.1336
Iteration: 2158; Percent complete: 53.9%; Average loss: 3.4318
Iteration: 2159; Percent complete: 54.0%; Average loss: 3.0707
Iteration: 2160; Percent complete: 54.0%; Average loss: 2.9642
Iteration: 2161; Percent complete: 54.0%; Average loss: 3.3021
Iteration: 2162; Percent complete: 54.0%; Average loss: 3.1535
Iteration: 2163; Percent complete: 54.1%; Average loss: 2.9975
Iteration: 2164; Percent complete: 54.1%; Average loss: 2.9110
Iteration: 2165; Percent complete: 54.1%; Average loss: 3.0378
Iteration: 2166; Percent complete: 54.1%; Average loss: 3.3520
Iteration: 2167; Percent complete: 54.2%; Average loss: 3.1600
Iteration: 2168; Percent complete: 54.2%; Average loss: 3.0805
Iteration: 2169; Percent complete: 54.2%; Average loss: 2.9637
Iteration: 2170; Percent complete: 54.2%; Average loss: 3.0738
Iteration: 2171; Percent complete: 54.3%; Average loss: 3.2978
Iteration: 2172; Percent complete: 54.3%; Average loss: 3.1923
Iteration: 2173; Percent complete: 54.3%; Average loss: 3.1148
Iteration: 2174; Percent complete: 54.4%; Average loss: 3.1870
Iteration: 2175; Percent complete: 54.4%; Average loss: 2.9133
Iteration: 2176; Percent complete: 54.4%; Average loss: 3.0286
Iteration: 2177; Percent complete: 54.4%; Average loss: 3.3070
Iteration: 2178; Percent complete: 54.4%; Average loss: 3.0740
Iteration: 2179; Percent complete: 54.5%; Average loss: 3.2147
Iteration: 2180; Percent complete: 54.5%; Average loss: 3.0348
Iteration: 2181; Percent complete: 54.5%; Average loss: 3.2399
Iteration: 2182; Percent complete: 54.5%; Average loss: 3.1020
Iteration: 2183; Percent complete: 54.6%; Average loss: 3.1017
Iteration: 2184; Percent complete: 54.6%; Average loss: 3.2629
Iteration: 2185; Percent complete: 54.6%; Average loss: 3.2930
Iteration: 2186; Percent complete: 54.6%; Average loss: 3.1091
Iteration: 2187; Percent complete: 54.7%; Average loss: 3.0081
Iteration: 2188; Percent complete: 54.7%; Average loss: 2.9237
Iteration: 2189; Percent complete: 54.7%; Average loss: 3.3645
Iteration: 2190; Percent complete: 54.8%; Average loss: 3.1014
Iteration: 2191; Percent complete: 54.8%; Average loss: 3.2780
Iteration: 2192; Percent complete: 54.8%; Average loss: 3.0768
Iteration: 2193; Percent complete: 54.8%; Average loss: 3.1018
Iteration: 2194; Percent complete: 54.9%; Average loss: 3.3537
Iteration: 2195; Percent complete: 54.9%; Average loss: 3.0785
Iteration: 2196; Percent complete: 54.9%; Average loss: 2.9488
Iteration: 2197; Percent complete: 54.9%; Average loss: 3.1202
Iteration: 2198; Percent complete: 54.9%; Average loss: 2.8679
Iteration: 2199; Percent complete: 55.0%; Average loss: 3.1388
Iteration: 2200; Percent complete: 55.0%; Average loss: 3.0005
Iteration: 2201; Percent complete: 55.0%; Average loss: 3.3011
Iteration: 2202; Percent complete: 55.0%; Average loss: 3.1734
Iteration: 2203; Percent complete: 55.1%; Average loss: 3.2128
Iteration: 2204; Percent complete: 55.1%; Average loss: 3.1434
Iteration: 2205; Percent complete: 55.1%; Average loss: 3.0864
Iteration: 2206; Percent complete: 55.1%; Average loss: 3.3262
Iteration: 2207; Percent complete: 55.2%; Average loss: 3.2159
Iteration: 2208; Percent complete: 55.2%; Average loss: 3.0292
Iteration: 2209; Percent complete: 55.2%; Average loss: 3.1982
Iteration: 2210; Percent complete: 55.2%; Average loss: 3.4010
Iteration: 2211; Percent complete: 55.3%; Average loss: 3.2263
Iteration: 2212; Percent complete: 55.3%; Average loss: 3.0017
Iteration: 2213; Percent complete: 55.3%; Average loss: 3.1004
Iteration: 2214; Percent complete: 55.4%; Average loss: 3.2078
Iteration: 2215; Percent complete: 55.4%; Average loss: 3.3354
Iteration: 2216; Percent complete: 55.4%; Average loss: 3.1285
Iteration: 2217; Percent complete: 55.4%; Average loss: 3.2564
Iteration: 2218; Percent complete: 55.5%; Average loss: 3.3035
Iteration: 2219; Percent complete: 55.5%; Average loss: 3.4079
Iteration: 2220; Percent complete: 55.5%; Average loss: 3.0544
Iteration: 2221; Percent complete: 55.5%; Average loss: 3.2701
Iteration: 2222; Percent complete: 55.5%; Average loss: 3.1974
Iteration: 2223; Percent complete: 55.6%; Average loss: 3.1396
Iteration: 2224; Percent complete: 55.6%; Average loss: 2.9782
Iteration: 2225; Percent complete: 55.6%; Average loss: 2.8853
Iteration: 2226; Percent complete: 55.6%; Average loss: 3.0045
Iteration: 2227; Percent complete: 55.7%; Average loss: 3.3025
Iteration: 2228; Percent complete: 55.7%; Average loss: 3.3157
Iteration: 2229; Percent complete: 55.7%; Average loss: 3.2005
Iteration: 2230; Percent complete: 55.8%; Average loss: 3.2122
Iteration: 2231; Percent complete: 55.8%; Average loss: 2.9437
Iteration: 2232; Percent complete: 55.8%; Average loss: 3.0209
Iteration: 2233; Percent complete: 55.8%; Average loss: 3.2632
Iteration: 2234; Percent complete: 55.9%; Average loss: 3.1353
Iteration: 2235; Percent complete: 55.9%; Average loss: 2.9669
Iteration: 2236; Percent complete: 55.9%; Average loss: 3.0427
Iteration: 2237; Percent complete: 55.9%; Average loss: 3.0453
Iteration: 2238; Percent complete: 56.0%; Average loss: 3.0238
Iteration: 2239; Percent complete: 56.0%; Average loss: 3.0327
Iteration: 2240; Percent complete: 56.0%; Average loss: 2.9858
Iteration: 2241; Percent complete: 56.0%; Average loss: 3.0507
Iteration: 2242; Percent complete: 56.0%; Average loss: 3.0321
Iteration: 2243; Percent complete: 56.1%; Average loss: 2.9986
Iteration: 2244; Percent complete: 56.1%; Average loss: 3.0765
Iteration: 2245; Percent complete: 56.1%; Average loss: 3.2777
Iteration: 2246; Percent complete: 56.1%; Average loss: 3.0901
Iteration: 2247; Percent complete: 56.2%; Average loss: 3.4724
Iteration: 2248; Percent complete: 56.2%; Average loss: 2.9829
Iteration: 2249; Percent complete: 56.2%; Average loss: 3.1272
Iteration: 2250; Percent complete: 56.2%; Average loss: 2.9402
Iteration: 2251; Percent complete: 56.3%; Average loss: 3.1554
Iteration: 2252; Percent complete: 56.3%; Average loss: 3.0994
Iteration: 2253; Percent complete: 56.3%; Average loss: 3.0655
Iteration: 2254; Percent complete: 56.4%; Average loss: 3.1600
Iteration: 2255; Percent complete: 56.4%; Average loss: 2.9469
Iteration: 2256; Percent complete: 56.4%; Average loss: 3.3004
Iteration: 2257; Percent complete: 56.4%; Average loss: 2.9893
Iteration: 2258; Percent complete: 56.5%; Average loss: 3.3306
Iteration: 2259; Percent complete: 56.5%; Average loss: 3.1550
Iteration: 2260; Percent complete: 56.5%; Average loss: 2.9485
Iteration: 2261; Percent complete: 56.5%; Average loss: 3.0657
Iteration: 2262; Percent complete: 56.5%; Average loss: 2.9529
Iteration: 2263; Percent complete: 56.6%; Average loss: 2.8067
Iteration: 2264; Percent complete: 56.6%; Average loss: 2.8875
Iteration: 2265; Percent complete: 56.6%; Average loss: 2.7577
Iteration: 2266; Percent complete: 56.6%; Average loss: 3.1396
Iteration: 2267; Percent complete: 56.7%; Average loss: 3.0551
Iteration: 2268; Percent complete: 56.7%; Average loss: 2.8371
Iteration: 2269; Percent complete: 56.7%; Average loss: 3.1672
Iteration: 2270; Percent complete: 56.8%; Average loss: 2.7546
Iteration: 2271; Percent complete: 56.8%; Average loss: 3.2824
Iteration: 2272; Percent complete: 56.8%; Average loss: 2.8875
Iteration: 2273; Percent complete: 56.8%; Average loss: 3.0945
Iteration: 2274; Percent complete: 56.9%; Average loss: 2.9042
Iteration: 2275; Percent complete: 56.9%; Average loss: 3.0260
Iteration: 2276; Percent complete: 56.9%; Average loss: 3.1075
Iteration: 2277; Percent complete: 56.9%; Average loss: 2.9884
Iteration: 2278; Percent complete: 57.0%; Average loss: 3.0911
Iteration: 2279; Percent complete: 57.0%; Average loss: 3.2201
Iteration: 2280; Percent complete: 57.0%; Average loss: 3.1462
Iteration: 2281; Percent complete: 57.0%; Average loss: 3.0280
Iteration: 2282; Percent complete: 57.0%; Average loss: 3.2981
Iteration: 2283; Percent complete: 57.1%; Average loss: 3.1970
Iteration: 2284; Percent complete: 57.1%; Average loss: 3.1961
Iteration: 2285; Percent complete: 57.1%; Average loss: 3.0491
Iteration: 2286; Percent complete: 57.1%; Average loss: 3.1367
Iteration: 2287; Percent complete: 57.2%; Average loss: 3.0118
Iteration: 2288; Percent complete: 57.2%; Average loss: 2.9669
Iteration: 2289; Percent complete: 57.2%; Average loss: 2.9276
Iteration: 2290; Percent complete: 57.2%; Average loss: 2.9916
Iteration: 2291; Percent complete: 57.3%; Average loss: 2.8422
Iteration: 2292; Percent complete: 57.3%; Average loss: 3.0177
Iteration: 2293; Percent complete: 57.3%; Average loss: 3.1425
Iteration: 2294; Percent complete: 57.4%; Average loss: 3.0965
Iteration: 2295; Percent complete: 57.4%; Average loss: 2.9676
Iteration: 2296; Percent complete: 57.4%; Average loss: 3.0381
Iteration: 2297; Percent complete: 57.4%; Average loss: 2.9624
Iteration: 2298; Percent complete: 57.5%; Average loss: 3.1283
Iteration: 2299; Percent complete: 57.5%; Average loss: 2.8518
Iteration: 2300; Percent complete: 57.5%; Average loss: 2.8693
Iteration: 2301; Percent complete: 57.5%; Average loss: 3.1559
Iteration: 2302; Percent complete: 57.6%; Average loss: 3.0744
Iteration: 2303; Percent complete: 57.6%; Average loss: 3.5840
Iteration: 2304; Percent complete: 57.6%; Average loss: 3.1481
Iteration: 2305; Percent complete: 57.6%; Average loss: 3.0606
Iteration: 2306; Percent complete: 57.6%; Average loss: 3.3495
Iteration: 2307; Percent complete: 57.7%; Average loss: 2.8560
Iteration: 2308; Percent complete: 57.7%; Average loss: 3.1087
Iteration: 2309; Percent complete: 57.7%; Average loss: 2.9871
Iteration: 2310; Percent complete: 57.8%; Average loss: 3.0565
Iteration: 2311; Percent complete: 57.8%; Average loss: 3.0440
Iteration: 2312; Percent complete: 57.8%; Average loss: 3.0977
Iteration: 2313; Percent complete: 57.8%; Average loss: 2.9603
Iteration: 2314; Percent complete: 57.9%; Average loss: 2.8540
Iteration: 2315; Percent complete: 57.9%; Average loss: 3.0491
Iteration: 2316; Percent complete: 57.9%; Average loss: 3.0249
Iteration: 2317; Percent complete: 57.9%; Average loss: 3.2601
Iteration: 2318; Percent complete: 58.0%; Average loss: 3.0521
Iteration: 2319; Percent complete: 58.0%; Average loss: 3.0214
Iteration: 2320; Percent complete: 58.0%; Average loss: 3.0129
Iteration: 2321; Percent complete: 58.0%; Average loss: 3.1648
Iteration: 2322; Percent complete: 58.1%; Average loss: 3.0367
Iteration: 2323; Percent complete: 58.1%; Average loss: 3.1871
Iteration: 2324; Percent complete: 58.1%; Average loss: 2.9711
Iteration: 2325; Percent complete: 58.1%; Average loss: 3.1409
Iteration: 2326; Percent complete: 58.1%; Average loss: 2.9978
Iteration: 2327; Percent complete: 58.2%; Average loss: 3.0263
Iteration: 2328; Percent complete: 58.2%; Average loss: 3.0475
Iteration: 2329; Percent complete: 58.2%; Average loss: 2.9264
Iteration: 2330; Percent complete: 58.2%; Average loss: 3.0390
Iteration: 2331; Percent complete: 58.3%; Average loss: 3.3543
Iteration: 2332; Percent complete: 58.3%; Average loss: 3.1628
Iteration: 2333; Percent complete: 58.3%; Average loss: 3.0674
Iteration: 2334; Percent complete: 58.4%; Average loss: 2.8974
Iteration: 2335; Percent complete: 58.4%; Average loss: 3.1183
Iteration: 2336; Percent complete: 58.4%; Average loss: 3.1210
Iteration: 2337; Percent complete: 58.4%; Average loss: 3.0941
Iteration: 2338; Percent complete: 58.5%; Average loss: 3.0673
Iteration: 2339; Percent complete: 58.5%; Average loss: 3.1776
Iteration: 2340; Percent complete: 58.5%; Average loss: 3.0430
Iteration: 2341; Percent complete: 58.5%; Average loss: 3.0147
Iteration: 2342; Percent complete: 58.6%; Average loss: 3.1374
Iteration: 2343; Percent complete: 58.6%; Average loss: 3.0963
Iteration: 2344; Percent complete: 58.6%; Average loss: 2.9072
Iteration: 2345; Percent complete: 58.6%; Average loss: 3.0712
Iteration: 2346; Percent complete: 58.7%; Average loss: 3.2709
Iteration: 2347; Percent complete: 58.7%; Average loss: 3.0919
Iteration: 2348; Percent complete: 58.7%; Average loss: 2.9601
Iteration: 2349; Percent complete: 58.7%; Average loss: 2.9953
Iteration: 2350; Percent complete: 58.8%; Average loss: 3.2328
Iteration: 2351; Percent complete: 58.8%; Average loss: 2.9388
Iteration: 2352; Percent complete: 58.8%; Average loss: 2.9755
Iteration: 2353; Percent complete: 58.8%; Average loss: 2.9686
Iteration: 2354; Percent complete: 58.9%; Average loss: 3.0631
Iteration: 2355; Percent complete: 58.9%; Average loss: 3.1811
Iteration: 2356; Percent complete: 58.9%; Average loss: 3.1079
Iteration: 2357; Percent complete: 58.9%; Average loss: 3.1047
Iteration: 2358; Percent complete: 59.0%; Average loss: 3.3455
Iteration: 2359; Percent complete: 59.0%; Average loss: 3.1228
Iteration: 2360; Percent complete: 59.0%; Average loss: 2.8534
Iteration: 2361; Percent complete: 59.0%; Average loss: 2.9343
Iteration: 2362; Percent complete: 59.1%; Average loss: 3.3347
Iteration: 2363; Percent complete: 59.1%; Average loss: 3.0743
Iteration: 2364; Percent complete: 59.1%; Average loss: 3.2456
Iteration: 2365; Percent complete: 59.1%; Average loss: 3.2557
Iteration: 2366; Percent complete: 59.2%; Average loss: 3.2765
Iteration: 2367; Percent complete: 59.2%; Average loss: 3.0285
Iteration: 2368; Percent complete: 59.2%; Average loss: 3.0135
Iteration: 2369; Percent complete: 59.2%; Average loss: 3.0921
Iteration: 2370; Percent complete: 59.2%; Average loss: 3.0613
Iteration: 2371; Percent complete: 59.3%; Average loss: 3.0797
Iteration: 2372; Percent complete: 59.3%; Average loss: 2.9207
Iteration: 2373; Percent complete: 59.3%; Average loss: 2.9138
Iteration: 2374; Percent complete: 59.4%; Average loss: 2.9570
Iteration: 2375; Percent complete: 59.4%; Average loss: 3.1796
Iteration: 2376; Percent complete: 59.4%; Average loss: 2.9961
Iteration: 2377; Percent complete: 59.4%; Average loss: 3.1264
Iteration: 2378; Percent complete: 59.5%; Average loss: 3.0517
Iteration: 2379; Percent complete: 59.5%; Average loss: 2.9126
Iteration: 2380; Percent complete: 59.5%; Average loss: 3.1177
Iteration: 2381; Percent complete: 59.5%; Average loss: 3.0937
Iteration: 2382; Percent complete: 59.6%; Average loss: 3.3794
Iteration: 2383; Percent complete: 59.6%; Average loss: 3.1702
Iteration: 2384; Percent complete: 59.6%; Average loss: 2.8897
Iteration: 2385; Percent complete: 59.6%; Average loss: 3.2160
Iteration: 2386; Percent complete: 59.7%; Average loss: 3.1787
Iteration: 2387; Percent complete: 59.7%; Average loss: 2.8632
Iteration: 2388; Percent complete: 59.7%; Average loss: 2.9499
Iteration: 2389; Percent complete: 59.7%; Average loss: 2.8470
Iteration: 2390; Percent complete: 59.8%; Average loss: 2.9747
Iteration: 2391; Percent complete: 59.8%; Average loss: 3.2598
Iteration: 2392; Percent complete: 59.8%; Average loss: 3.1489
Iteration: 2393; Percent complete: 59.8%; Average loss: 3.2288
Iteration: 2394; Percent complete: 59.9%; Average loss: 2.9331
Iteration: 2395; Percent complete: 59.9%; Average loss: 3.0579
Iteration: 2396; Percent complete: 59.9%; Average loss: 3.1110
Iteration: 2397; Percent complete: 59.9%; Average loss: 2.8063
Iteration: 2398; Percent complete: 60.0%; Average loss: 3.2140
Iteration: 2399; Percent complete: 60.0%; Average loss: 2.8330
Iteration: 2400; Percent complete: 60.0%; Average loss: 2.6276
Iteration: 2401; Percent complete: 60.0%; Average loss: 2.9270
Iteration: 2402; Percent complete: 60.1%; Average loss: 2.8858
Iteration: 2403; Percent complete: 60.1%; Average loss: 2.8122
Iteration: 2404; Percent complete: 60.1%; Average loss: 2.7633
Iteration: 2405; Percent complete: 60.1%; Average loss: 3.2093
Iteration: 2406; Percent complete: 60.2%; Average loss: 3.1593
Iteration: 2407; Percent complete: 60.2%; Average loss: 3.1181
Iteration: 2408; Percent complete: 60.2%; Average loss: 3.0190
Iteration: 2409; Percent complete: 60.2%; Average loss: 3.1849
Iteration: 2410; Percent complete: 60.2%; Average loss: 2.9970
Iteration: 2411; Percent complete: 60.3%; Average loss: 3.0036
Iteration: 2412; Percent complete: 60.3%; Average loss: 3.2381
Iteration: 2413; Percent complete: 60.3%; Average loss: 3.2872
Iteration: 2414; Percent complete: 60.4%; Average loss: 3.3101
Iteration: 2415; Percent complete: 60.4%; Average loss: 3.1739
Iteration: 2416; Percent complete: 60.4%; Average loss: 3.1755
Iteration: 2417; Percent complete: 60.4%; Average loss: 3.1347
Iteration: 2418; Percent complete: 60.5%; Average loss: 3.2006
Iteration: 2419; Percent complete: 60.5%; Average loss: 3.2018
Iteration: 2420; Percent complete: 60.5%; Average loss: 3.1839
Iteration: 2421; Percent complete: 60.5%; Average loss: 3.1486
Iteration: 2422; Percent complete: 60.6%; Average loss: 2.9655
Iteration: 2423; Percent complete: 60.6%; Average loss: 3.0758
Iteration: 2424; Percent complete: 60.6%; Average loss: 2.7798
Iteration: 2425; Percent complete: 60.6%; Average loss: 2.9359
Iteration: 2426; Percent complete: 60.7%; Average loss: 2.9993
Iteration: 2427; Percent complete: 60.7%; Average loss: 2.9335
Iteration: 2428; Percent complete: 60.7%; Average loss: 2.8439
Iteration: 2429; Percent complete: 60.7%; Average loss: 3.1883
Iteration: 2430; Percent complete: 60.8%; Average loss: 3.0873
Iteration: 2431; Percent complete: 60.8%; Average loss: 2.8946
Iteration: 2432; Percent complete: 60.8%; Average loss: 3.0565
Iteration: 2433; Percent complete: 60.8%; Average loss: 2.9284
Iteration: 2434; Percent complete: 60.9%; Average loss: 3.0506
Iteration: 2435; Percent complete: 60.9%; Average loss: 3.0819
Iteration: 2436; Percent complete: 60.9%; Average loss: 2.9589
Iteration: 2437; Percent complete: 60.9%; Average loss: 3.1483
Iteration: 2438; Percent complete: 61.0%; Average loss: 2.8091
Iteration: 2439; Percent complete: 61.0%; Average loss: 2.8599
Iteration: 2440; Percent complete: 61.0%; Average loss: 2.8702
Iteration: 2441; Percent complete: 61.0%; Average loss: 2.8782
Iteration: 2442; Percent complete: 61.1%; Average loss: 2.9520
Iteration: 2443; Percent complete: 61.1%; Average loss: 3.0145
Iteration: 2444; Percent complete: 61.1%; Average loss: 3.0503
Iteration: 2445; Percent complete: 61.1%; Average loss: 2.8946
Iteration: 2446; Percent complete: 61.2%; Average loss: 3.0827
Iteration: 2447; Percent complete: 61.2%; Average loss: 3.0129
Iteration: 2448; Percent complete: 61.2%; Average loss: 2.8630
Iteration: 2449; Percent complete: 61.2%; Average loss: 2.7709
Iteration: 2450; Percent complete: 61.3%; Average loss: 2.9828
Iteration: 2451; Percent complete: 61.3%; Average loss: 2.8671
Iteration: 2452; Percent complete: 61.3%; Average loss: 2.9595
Iteration: 2453; Percent complete: 61.3%; Average loss: 3.0525
Iteration: 2454; Percent complete: 61.4%; Average loss: 3.1900
Iteration: 2455; Percent complete: 61.4%; Average loss: 2.9481
Iteration: 2456; Percent complete: 61.4%; Average loss: 2.9968
Iteration: 2457; Percent complete: 61.4%; Average loss: 3.0558
Iteration: 2458; Percent complete: 61.5%; Average loss: 3.2430
Iteration: 2459; Percent complete: 61.5%; Average loss: 3.1863
Iteration: 2460; Percent complete: 61.5%; Average loss: 3.0906
Iteration: 2461; Percent complete: 61.5%; Average loss: 3.0319
Iteration: 2462; Percent complete: 61.6%; Average loss: 2.8962
Iteration: 2463; Percent complete: 61.6%; Average loss: 2.9671
Iteration: 2464; Percent complete: 61.6%; Average loss: 2.8474
Iteration: 2465; Percent complete: 61.6%; Average loss: 2.9620
Iteration: 2466; Percent complete: 61.7%; Average loss: 3.1780
Iteration: 2467; Percent complete: 61.7%; Average loss: 2.7869
Iteration: 2468; Percent complete: 61.7%; Average loss: 2.9581
Iteration: 2469; Percent complete: 61.7%; Average loss: 2.9532
Iteration: 2470; Percent complete: 61.8%; Average loss: 2.8665
Iteration: 2471; Percent complete: 61.8%; Average loss: 3.2206
Iteration: 2472; Percent complete: 61.8%; Average loss: 2.9327
Iteration: 2473; Percent complete: 61.8%; Average loss: 3.1918
Iteration: 2474; Percent complete: 61.9%; Average loss: 3.0657
Iteration: 2475; Percent complete: 61.9%; Average loss: 2.7956
Iteration: 2476; Percent complete: 61.9%; Average loss: 3.3250
Iteration: 2477; Percent complete: 61.9%; Average loss: 2.7548
Iteration: 2478; Percent complete: 62.0%; Average loss: 3.0801
Iteration: 2479; Percent complete: 62.0%; Average loss: 3.3079
Iteration: 2480; Percent complete: 62.0%; Average loss: 3.1212
Iteration: 2481; Percent complete: 62.0%; Average loss: 3.2734
Iteration: 2482; Percent complete: 62.1%; Average loss: 3.2004
Iteration: 2483; Percent complete: 62.1%; Average loss: 2.9610
Iteration: 2484; Percent complete: 62.1%; Average loss: 2.9961
Iteration: 2485; Percent complete: 62.1%; Average loss: 3.0607
Iteration: 2486; Percent complete: 62.2%; Average loss: 2.9582
Iteration: 2487; Percent complete: 62.2%; Average loss: 3.1343
Iteration: 2488; Percent complete: 62.2%; Average loss: 2.7305
Iteration: 2489; Percent complete: 62.2%; Average loss: 2.9155
Iteration: 2490; Percent complete: 62.3%; Average loss: 3.0202
Iteration: 2491; Percent complete: 62.3%; Average loss: 3.0771
Iteration: 2492; Percent complete: 62.3%; Average loss: 3.1420
Iteration: 2493; Percent complete: 62.3%; Average loss: 3.0193
Iteration: 2494; Percent complete: 62.4%; Average loss: 3.4035
Iteration: 2495; Percent complete: 62.4%; Average loss: 3.1947
Iteration: 2496; Percent complete: 62.4%; Average loss: 2.9818
Iteration: 2497; Percent complete: 62.4%; Average loss: 3.1323
Iteration: 2498; Percent complete: 62.5%; Average loss: 3.0116
Iteration: 2499; Percent complete: 62.5%; Average loss: 3.0547
Iteration: 2500; Percent complete: 62.5%; Average loss: 3.1208
Iteration: 2501; Percent complete: 62.5%; Average loss: 2.9272
Iteration: 2502; Percent complete: 62.5%; Average loss: 3.0132
Iteration: 2503; Percent complete: 62.6%; Average loss: 3.1009
Iteration: 2504; Percent complete: 62.6%; Average loss: 2.9200
Iteration: 2505; Percent complete: 62.6%; Average loss: 3.0357
Iteration: 2506; Percent complete: 62.6%; Average loss: 2.9920
Iteration: 2507; Percent complete: 62.7%; Average loss: 3.1509
Iteration: 2508; Percent complete: 62.7%; Average loss: 3.0554
Iteration: 2509; Percent complete: 62.7%; Average loss: 2.9264
Iteration: 2510; Percent complete: 62.7%; Average loss: 2.8918
Iteration: 2511; Percent complete: 62.8%; Average loss: 2.8787
Iteration: 2512; Percent complete: 62.8%; Average loss: 3.0643
Iteration: 2513; Percent complete: 62.8%; Average loss: 3.0849
Iteration: 2514; Percent complete: 62.8%; Average loss: 2.7627
Iteration: 2515; Percent complete: 62.9%; Average loss: 2.8769
Iteration: 2516; Percent complete: 62.9%; Average loss: 2.9891
Iteration: 2517; Percent complete: 62.9%; Average loss: 3.2234
Iteration: 2518; Percent complete: 62.9%; Average loss: 2.9998
Iteration: 2519; Percent complete: 63.0%; Average loss: 3.2389
Iteration: 2520; Percent complete: 63.0%; Average loss: 2.7432
Iteration: 2521; Percent complete: 63.0%; Average loss: 3.1679
Iteration: 2522; Percent complete: 63.0%; Average loss: 2.9294
Iteration: 2523; Percent complete: 63.1%; Average loss: 3.1141
Iteration: 2524; Percent complete: 63.1%; Average loss: 2.8740
Iteration: 2525; Percent complete: 63.1%; Average loss: 3.0579
Iteration: 2526; Percent complete: 63.1%; Average loss: 2.9340
Iteration: 2527; Percent complete: 63.2%; Average loss: 3.2002
Iteration: 2528; Percent complete: 63.2%; Average loss: 2.9268
Iteration: 2529; Percent complete: 63.2%; Average loss: 3.0641
Iteration: 2530; Percent complete: 63.2%; Average loss: 3.1626
Iteration: 2531; Percent complete: 63.3%; Average loss: 2.9727
Iteration: 2532; Percent complete: 63.3%; Average loss: 2.9524
Iteration: 2533; Percent complete: 63.3%; Average loss: 3.1508
Iteration: 2534; Percent complete: 63.3%; Average loss: 2.8703
Iteration: 2535; Percent complete: 63.4%; Average loss: 3.1149
Iteration: 2536; Percent complete: 63.4%; Average loss: 3.0004
Iteration: 2537; Percent complete: 63.4%; Average loss: 2.7679
Iteration: 2538; Percent complete: 63.4%; Average loss: 3.1417
Iteration: 2539; Percent complete: 63.5%; Average loss: 3.1795
Iteration: 2540; Percent complete: 63.5%; Average loss: 3.0486
Iteration: 2541; Percent complete: 63.5%; Average loss: 3.0379
Iteration: 2542; Percent complete: 63.5%; Average loss: 2.9293
Iteration: 2543; Percent complete: 63.6%; Average loss: 3.1080
Iteration: 2544; Percent complete: 63.6%; Average loss: 2.9414
Iteration: 2545; Percent complete: 63.6%; Average loss: 3.0494
Iteration: 2546; Percent complete: 63.6%; Average loss: 2.8406
Iteration: 2547; Percent complete: 63.7%; Average loss: 3.1494
Iteration: 2548; Percent complete: 63.7%; Average loss: 3.3226
Iteration: 2549; Percent complete: 63.7%; Average loss: 3.0570
Iteration: 2550; Percent complete: 63.7%; Average loss: 2.7335
Iteration: 2551; Percent complete: 63.8%; Average loss: 2.8703
Iteration: 2552; Percent complete: 63.8%; Average loss: 2.7747
Iteration: 2553; Percent complete: 63.8%; Average loss: 2.9505
Iteration: 2554; Percent complete: 63.8%; Average loss: 2.9247
Iteration: 2555; Percent complete: 63.9%; Average loss: 3.1361
Iteration: 2556; Percent complete: 63.9%; Average loss: 3.0360
Iteration: 2557; Percent complete: 63.9%; Average loss: 3.0888
Iteration: 2558; Percent complete: 63.9%; Average loss: 2.9720
Iteration: 2559; Percent complete: 64.0%; Average loss: 2.9590
Iteration: 2560; Percent complete: 64.0%; Average loss: 2.9623
Iteration: 2561; Percent complete: 64.0%; Average loss: 3.0323
Iteration: 2562; Percent complete: 64.0%; Average loss: 3.1154
Iteration: 2563; Percent complete: 64.1%; Average loss: 2.8849
Iteration: 2564; Percent complete: 64.1%; Average loss: 3.0606
Iteration: 2565; Percent complete: 64.1%; Average loss: 2.9294
Iteration: 2566; Percent complete: 64.1%; Average loss: 2.8491
Iteration: 2567; Percent complete: 64.2%; Average loss: 3.0578
Iteration: 2568; Percent complete: 64.2%; Average loss: 3.1109
Iteration: 2569; Percent complete: 64.2%; Average loss: 3.0345
Iteration: 2570; Percent complete: 64.2%; Average loss: 3.0716
Iteration: 2571; Percent complete: 64.3%; Average loss: 2.9402
Iteration: 2572; Percent complete: 64.3%; Average loss: 3.0223
Iteration: 2573; Percent complete: 64.3%; Average loss: 2.9336
Iteration: 2574; Percent complete: 64.3%; Average loss: 3.0507
Iteration: 2575; Percent complete: 64.4%; Average loss: 2.8489
Iteration: 2576; Percent complete: 64.4%; Average loss: 2.8677
Iteration: 2577; Percent complete: 64.4%; Average loss: 2.8614
Iteration: 2578; Percent complete: 64.5%; Average loss: 2.9007
Iteration: 2579; Percent complete: 64.5%; Average loss: 2.9934
Iteration: 2580; Percent complete: 64.5%; Average loss: 3.0952
Iteration: 2581; Percent complete: 64.5%; Average loss: 3.1043
Iteration: 2582; Percent complete: 64.5%; Average loss: 2.9951
Iteration: 2583; Percent complete: 64.6%; Average loss: 2.9833
Iteration: 2584; Percent complete: 64.6%; Average loss: 3.0538
Iteration: 2585; Percent complete: 64.6%; Average loss: 2.9989
Iteration: 2586; Percent complete: 64.6%; Average loss: 3.0041
Iteration: 2587; Percent complete: 64.7%; Average loss: 3.2070
Iteration: 2588; Percent complete: 64.7%; Average loss: 3.0560
Iteration: 2589; Percent complete: 64.7%; Average loss: 2.7698
Iteration: 2590; Percent complete: 64.8%; Average loss: 3.0419
Iteration: 2591; Percent complete: 64.8%; Average loss: 3.1482
Iteration: 2592; Percent complete: 64.8%; Average loss: 3.1031
Iteration: 2593; Percent complete: 64.8%; Average loss: 2.9887
Iteration: 2594; Percent complete: 64.8%; Average loss: 3.1984
Iteration: 2595; Percent complete: 64.9%; Average loss: 3.0237
Iteration: 2596; Percent complete: 64.9%; Average loss: 2.9036
Iteration: 2597; Percent complete: 64.9%; Average loss: 3.0277
Iteration: 2598; Percent complete: 65.0%; Average loss: 2.8764
Iteration: 2599; Percent complete: 65.0%; Average loss: 2.9566
Iteration: 2600; Percent complete: 65.0%; Average loss: 3.1089
Iteration: 2601; Percent complete: 65.0%; Average loss: 2.7900
Iteration: 2602; Percent complete: 65.0%; Average loss: 2.7458
Iteration: 2603; Percent complete: 65.1%; Average loss: 2.6738
Iteration: 2604; Percent complete: 65.1%; Average loss: 2.8989
Iteration: 2605; Percent complete: 65.1%; Average loss: 3.0168
Iteration: 2606; Percent complete: 65.1%; Average loss: 2.8470
Iteration: 2607; Percent complete: 65.2%; Average loss: 2.9829
Iteration: 2608; Percent complete: 65.2%; Average loss: 3.0253
Iteration: 2609; Percent complete: 65.2%; Average loss: 2.9534
Iteration: 2610; Percent complete: 65.2%; Average loss: 2.9634
Iteration: 2611; Percent complete: 65.3%; Average loss: 3.0043
Iteration: 2612; Percent complete: 65.3%; Average loss: 3.2132
Iteration: 2613; Percent complete: 65.3%; Average loss: 2.9449
Iteration: 2614; Percent complete: 65.3%; Average loss: 2.9361
Iteration: 2615; Percent complete: 65.4%; Average loss: 3.0048
Iteration: 2616; Percent complete: 65.4%; Average loss: 2.9494
Iteration: 2617; Percent complete: 65.4%; Average loss: 2.9781
Iteration: 2618; Percent complete: 65.5%; Average loss: 3.0246
Iteration: 2619; Percent complete: 65.5%; Average loss: 2.9185
Iteration: 2620; Percent complete: 65.5%; Average loss: 3.1942
Iteration: 2621; Percent complete: 65.5%; Average loss: 2.8708
Iteration: 2622; Percent complete: 65.5%; Average loss: 2.8498
Iteration: 2623; Percent complete: 65.6%; Average loss: 2.9054
Iteration: 2624; Percent complete: 65.6%; Average loss: 2.8807
Iteration: 2625; Percent complete: 65.6%; Average loss: 3.1079
Iteration: 2626; Percent complete: 65.6%; Average loss: 2.9385
Iteration: 2627; Percent complete: 65.7%; Average loss: 2.9598
Iteration: 2628; Percent complete: 65.7%; Average loss: 3.0057
Iteration: 2629; Percent complete: 65.7%; Average loss: 2.7460
Iteration: 2630; Percent complete: 65.8%; Average loss: 2.9569
Iteration: 2631; Percent complete: 65.8%; Average loss: 3.2183
Iteration: 2632; Percent complete: 65.8%; Average loss: 2.8805
Iteration: 2633; Percent complete: 65.8%; Average loss: 2.9737
Iteration: 2634; Percent complete: 65.8%; Average loss: 2.9696
Iteration: 2635; Percent complete: 65.9%; Average loss: 3.0761
Iteration: 2636; Percent complete: 65.9%; Average loss: 2.8527
Iteration: 2637; Percent complete: 65.9%; Average loss: 2.9134
Iteration: 2638; Percent complete: 66.0%; Average loss: 2.7805
Iteration: 2639; Percent complete: 66.0%; Average loss: 2.8107
Iteration: 2640; Percent complete: 66.0%; Average loss: 2.8765
Iteration: 2641; Percent complete: 66.0%; Average loss: 2.9266
Iteration: 2642; Percent complete: 66.0%; Average loss: 3.0979
Iteration: 2643; Percent complete: 66.1%; Average loss: 3.0825
Iteration: 2644; Percent complete: 66.1%; Average loss: 2.8690
Iteration: 2645; Percent complete: 66.1%; Average loss: 3.0581
Iteration: 2646; Percent complete: 66.1%; Average loss: 3.3303
Iteration: 2647; Percent complete: 66.2%; Average loss: 2.9708
Iteration: 2648; Percent complete: 66.2%; Average loss: 2.9205
Iteration: 2649; Percent complete: 66.2%; Average loss: 2.8475
Iteration: 2650; Percent complete: 66.2%; Average loss: 2.8464
Iteration: 2651; Percent complete: 66.3%; Average loss: 2.9109
Iteration: 2652; Percent complete: 66.3%; Average loss: 3.1002
Iteration: 2653; Percent complete: 66.3%; Average loss: 2.9051
Iteration: 2654; Percent complete: 66.3%; Average loss: 2.7124
Iteration: 2655; Percent complete: 66.4%; Average loss: 2.9598
Iteration: 2656; Percent complete: 66.4%; Average loss: 3.1238
Iteration: 2657; Percent complete: 66.4%; Average loss: 2.9042
Iteration: 2658; Percent complete: 66.5%; Average loss: 2.7146
Iteration: 2659; Percent complete: 66.5%; Average loss: 3.1985
Iteration: 2660; Percent complete: 66.5%; Average loss: 3.0106
Iteration: 2661; Percent complete: 66.5%; Average loss: 2.9800
Iteration: 2662; Percent complete: 66.5%; Average loss: 2.8487
Iteration: 2663; Percent complete: 66.6%; Average loss: 3.2439
Iteration: 2664; Percent complete: 66.6%; Average loss: 2.9203
Iteration: 2665; Percent complete: 66.6%; Average loss: 3.0507
Iteration: 2666; Percent complete: 66.6%; Average loss: 2.8152
Iteration: 2667; Percent complete: 66.7%; Average loss: 2.9897
Iteration: 2668; Percent complete: 66.7%; Average loss: 2.9201
Iteration: 2669; Percent complete: 66.7%; Average loss: 3.1326
Iteration: 2670; Percent complete: 66.8%; Average loss: 3.1321
Iteration: 2671; Percent complete: 66.8%; Average loss: 2.8922
Iteration: 2672; Percent complete: 66.8%; Average loss: 3.1120
Iteration: 2673; Percent complete: 66.8%; Average loss: 3.0737
Iteration: 2674; Percent complete: 66.8%; Average loss: 2.8217
Iteration: 2675; Percent complete: 66.9%; Average loss: 2.9388
Iteration: 2676; Percent complete: 66.9%; Average loss: 2.9427
Iteration: 2677; Percent complete: 66.9%; Average loss: 2.8654
Iteration: 2678; Percent complete: 67.0%; Average loss: 2.9572
Iteration: 2679; Percent complete: 67.0%; Average loss: 2.7805
Iteration: 2680; Percent complete: 67.0%; Average loss: 3.0924
Iteration: 2681; Percent complete: 67.0%; Average loss: 2.7122
Iteration: 2682; Percent complete: 67.0%; Average loss: 2.9333
Iteration: 2683; Percent complete: 67.1%; Average loss: 2.8752
Iteration: 2684; Percent complete: 67.1%; Average loss: 2.8858
Iteration: 2685; Percent complete: 67.1%; Average loss: 2.8488
Iteration: 2686; Percent complete: 67.2%; Average loss: 2.8947
Iteration: 2687; Percent complete: 67.2%; Average loss: 3.0614
Iteration: 2688; Percent complete: 67.2%; Average loss: 2.8792
Iteration: 2689; Percent complete: 67.2%; Average loss: 2.8583
Iteration: 2690; Percent complete: 67.2%; Average loss: 3.0570
Iteration: 2691; Percent complete: 67.3%; Average loss: 2.7072
Iteration: 2692; Percent complete: 67.3%; Average loss: 3.0465
Iteration: 2693; Percent complete: 67.3%; Average loss: 3.3506
Iteration: 2694; Percent complete: 67.3%; Average loss: 3.1131
Iteration: 2695; Percent complete: 67.4%; Average loss: 3.0464
Iteration: 2696; Percent complete: 67.4%; Average loss: 2.8742
Iteration: 2697; Percent complete: 67.4%; Average loss: 2.9434
Iteration: 2698; Percent complete: 67.5%; Average loss: 3.0800
Iteration: 2699; Percent complete: 67.5%; Average loss: 2.7331
Iteration: 2700; Percent complete: 67.5%; Average loss: 2.8734
Iteration: 2701; Percent complete: 67.5%; Average loss: 3.0558
Iteration: 2702; Percent complete: 67.5%; Average loss: 2.8178
Iteration: 2703; Percent complete: 67.6%; Average loss: 2.8020
Iteration: 2704; Percent complete: 67.6%; Average loss: 3.2916
Iteration: 2705; Percent complete: 67.6%; Average loss: 2.7407
Iteration: 2706; Percent complete: 67.7%; Average loss: 2.7595
Iteration: 2707; Percent complete: 67.7%; Average loss: 2.7492
Iteration: 2708; Percent complete: 67.7%; Average loss: 2.9225
Iteration: 2709; Percent complete: 67.7%; Average loss: 3.1440
Iteration: 2710; Percent complete: 67.8%; Average loss: 2.9234
Iteration: 2711; Percent complete: 67.8%; Average loss: 2.9843
Iteration: 2712; Percent complete: 67.8%; Average loss: 3.0214
Iteration: 2713; Percent complete: 67.8%; Average loss: 3.0157
Iteration: 2714; Percent complete: 67.8%; Average loss: 3.0435
Iteration: 2715; Percent complete: 67.9%; Average loss: 3.0555
Iteration: 2716; Percent complete: 67.9%; Average loss: 2.9009
Iteration: 2717; Percent complete: 67.9%; Average loss: 2.6602
Iteration: 2718; Percent complete: 68.0%; Average loss: 2.7884
Iteration: 2719; Percent complete: 68.0%; Average loss: 2.9220
Iteration: 2720; Percent complete: 68.0%; Average loss: 2.8660
Iteration: 2721; Percent complete: 68.0%; Average loss: 2.9431
Iteration: 2722; Percent complete: 68.0%; Average loss: 2.9566
Iteration: 2723; Percent complete: 68.1%; Average loss: 3.1285
Iteration: 2724; Percent complete: 68.1%; Average loss: 3.0617
Iteration: 2725; Percent complete: 68.1%; Average loss: 3.1707
Iteration: 2726; Percent complete: 68.2%; Average loss: 2.7747
Iteration: 2727; Percent complete: 68.2%; Average loss: 3.0770
Iteration: 2728; Percent complete: 68.2%; Average loss: 2.7956
Iteration: 2729; Percent complete: 68.2%; Average loss: 2.8039
Iteration: 2730; Percent complete: 68.2%; Average loss: 3.0310
Iteration: 2731; Percent complete: 68.3%; Average loss: 2.8912
Iteration: 2732; Percent complete: 68.3%; Average loss: 3.0607
Iteration: 2733; Percent complete: 68.3%; Average loss: 2.9436
Iteration: 2734; Percent complete: 68.3%; Average loss: 3.1030
Iteration: 2735; Percent complete: 68.4%; Average loss: 2.7918
Iteration: 2736; Percent complete: 68.4%; Average loss: 3.0495
Iteration: 2737; Percent complete: 68.4%; Average loss: 2.8687
Iteration: 2738; Percent complete: 68.5%; Average loss: 2.8783
Iteration: 2739; Percent complete: 68.5%; Average loss: 2.9401
Iteration: 2740; Percent complete: 68.5%; Average loss: 3.0822
Iteration: 2741; Percent complete: 68.5%; Average loss: 2.7003
Iteration: 2742; Percent complete: 68.5%; Average loss: 3.0849
Iteration: 2743; Percent complete: 68.6%; Average loss: 2.8432
Iteration: 2744; Percent complete: 68.6%; Average loss: 3.0613
Iteration: 2745; Percent complete: 68.6%; Average loss: 3.2078
Iteration: 2746; Percent complete: 68.7%; Average loss: 2.8391
Iteration: 2747; Percent complete: 68.7%; Average loss: 2.6509
Iteration: 2748; Percent complete: 68.7%; Average loss: 2.6794
Iteration: 2749; Percent complete: 68.7%; Average loss: 2.9220
Iteration: 2750; Percent complete: 68.8%; Average loss: 2.9493
Iteration: 2751; Percent complete: 68.8%; Average loss: 2.8599
Iteration: 2752; Percent complete: 68.8%; Average loss: 3.0130
Iteration: 2753; Percent complete: 68.8%; Average loss: 2.8766
Iteration: 2754; Percent complete: 68.8%; Average loss: 2.8618
Iteration: 2755; Percent complete: 68.9%; Average loss: 3.1393
Iteration: 2756; Percent complete: 68.9%; Average loss: 2.8032
Iteration: 2757; Percent complete: 68.9%; Average loss: 3.0473
Iteration: 2758; Percent complete: 69.0%; Average loss: 3.2338
Iteration: 2759; Percent complete: 69.0%; Average loss: 2.8036
Iteration: 2760; Percent complete: 69.0%; Average loss: 2.9282
Iteration: 2761; Percent complete: 69.0%; Average loss: 2.9594
Iteration: 2762; Percent complete: 69.0%; Average loss: 2.8012
Iteration: 2763; Percent complete: 69.1%; Average loss: 2.9509
Iteration: 2764; Percent complete: 69.1%; Average loss: 2.9350
Iteration: 2765; Percent complete: 69.1%; Average loss: 2.8643
Iteration: 2766; Percent complete: 69.2%; Average loss: 3.0158
Iteration: 2767; Percent complete: 69.2%; Average loss: 2.9344
Iteration: 2768; Percent complete: 69.2%; Average loss: 2.8203
Iteration: 2769; Percent complete: 69.2%; Average loss: 3.1942
Iteration: 2770; Percent complete: 69.2%; Average loss: 3.0070
Iteration: 2771; Percent complete: 69.3%; Average loss: 2.9381
Iteration: 2772; Percent complete: 69.3%; Average loss: 3.0409
Iteration: 2773; Percent complete: 69.3%; Average loss: 2.7463
Iteration: 2774; Percent complete: 69.3%; Average loss: 3.0827
Iteration: 2775; Percent complete: 69.4%; Average loss: 2.8442
Iteration: 2776; Percent complete: 69.4%; Average loss: 3.0141
Iteration: 2777; Percent complete: 69.4%; Average loss: 3.2356
Iteration: 2778; Percent complete: 69.5%; Average loss: 2.8445
Iteration: 2779; Percent complete: 69.5%; Average loss: 3.0121
Iteration: 2780; Percent complete: 69.5%; Average loss: 3.0454
Iteration: 2781; Percent complete: 69.5%; Average loss: 2.8974
Iteration: 2782; Percent complete: 69.5%; Average loss: 3.0758
Iteration: 2783; Percent complete: 69.6%; Average loss: 2.9280
Iteration: 2784; Percent complete: 69.6%; Average loss: 2.6616
Iteration: 2785; Percent complete: 69.6%; Average loss: 2.9185
Iteration: 2786; Percent complete: 69.7%; Average loss: 3.0811
Iteration: 2787; Percent complete: 69.7%; Average loss: 3.0269
Iteration: 2788; Percent complete: 69.7%; Average loss: 2.8774
Iteration: 2789; Percent complete: 69.7%; Average loss: 2.9482
Iteration: 2790; Percent complete: 69.8%; Average loss: 2.9628
Iteration: 2791; Percent complete: 69.8%; Average loss: 2.9328
Iteration: 2792; Percent complete: 69.8%; Average loss: 3.0841
Iteration: 2793; Percent complete: 69.8%; Average loss: 2.9237
Iteration: 2794; Percent complete: 69.8%; Average loss: 2.9656
Iteration: 2795; Percent complete: 69.9%; Average loss: 2.8365
Iteration: 2796; Percent complete: 69.9%; Average loss: 2.9331
Iteration: 2797; Percent complete: 69.9%; Average loss: 3.1752
Iteration: 2798; Percent complete: 70.0%; Average loss: 2.7641
Iteration: 2799; Percent complete: 70.0%; Average loss: 3.0632
Iteration: 2800; Percent complete: 70.0%; Average loss: 3.0819
Iteration: 2801; Percent complete: 70.0%; Average loss: 2.9706
Iteration: 2802; Percent complete: 70.0%; Average loss: 2.9242
Iteration: 2803; Percent complete: 70.1%; Average loss: 2.8088
Iteration: 2804; Percent complete: 70.1%; Average loss: 2.7531
Iteration: 2805; Percent complete: 70.1%; Average loss: 2.8253
Iteration: 2806; Percent complete: 70.2%; Average loss: 3.0027
Iteration: 2807; Percent complete: 70.2%; Average loss: 2.9430
Iteration: 2808; Percent complete: 70.2%; Average loss: 3.0763
Iteration: 2809; Percent complete: 70.2%; Average loss: 2.8889
Iteration: 2810; Percent complete: 70.2%; Average loss: 2.7613
Iteration: 2811; Percent complete: 70.3%; Average loss: 3.2227
Iteration: 2812; Percent complete: 70.3%; Average loss: 2.5932
Iteration: 2813; Percent complete: 70.3%; Average loss: 2.7558
Iteration: 2814; Percent complete: 70.3%; Average loss: 2.8189
Iteration: 2815; Percent complete: 70.4%; Average loss: 2.9784
Iteration: 2816; Percent complete: 70.4%; Average loss: 2.9589
Iteration: 2817; Percent complete: 70.4%; Average loss: 3.0670
Iteration: 2818; Percent complete: 70.5%; Average loss: 2.8677
Iteration: 2819; Percent complete: 70.5%; Average loss: 2.8173
Iteration: 2820; Percent complete: 70.5%; Average loss: 2.9135
Iteration: 2821; Percent complete: 70.5%; Average loss: 2.8151
Iteration: 2822; Percent complete: 70.5%; Average loss: 2.9716
Iteration: 2823; Percent complete: 70.6%; Average loss: 3.0680
Iteration: 2824; Percent complete: 70.6%; Average loss: 3.0947
Iteration: 2825; Percent complete: 70.6%; Average loss: 2.7318
Iteration: 2826; Percent complete: 70.7%; Average loss: 2.9403
Iteration: 2827; Percent complete: 70.7%; Average loss: 2.7785
Iteration: 2828; Percent complete: 70.7%; Average loss: 2.8467
Iteration: 2829; Percent complete: 70.7%; Average loss: 2.7763
Iteration: 2830; Percent complete: 70.8%; Average loss: 2.8120
Iteration: 2831; Percent complete: 70.8%; Average loss: 2.6759
Iteration: 2832; Percent complete: 70.8%; Average loss: 2.6231
Iteration: 2833; Percent complete: 70.8%; Average loss: 2.9721
Iteration: 2834; Percent complete: 70.9%; Average loss: 2.9431
Iteration: 2835; Percent complete: 70.9%; Average loss: 2.8166
Iteration: 2836; Percent complete: 70.9%; Average loss: 3.0912
Iteration: 2837; Percent complete: 70.9%; Average loss: 2.7830
Iteration: 2838; Percent complete: 71.0%; Average loss: 2.7182
Iteration: 2839; Percent complete: 71.0%; Average loss: 2.8689
Iteration: 2840; Percent complete: 71.0%; Average loss: 2.8863
Iteration: 2841; Percent complete: 71.0%; Average loss: 2.8918
Iteration: 2842; Percent complete: 71.0%; Average loss: 2.8485
Iteration: 2843; Percent complete: 71.1%; Average loss: 2.9031
Iteration: 2844; Percent complete: 71.1%; Average loss: 3.1673
Iteration: 2845; Percent complete: 71.1%; Average loss: 2.9412
Iteration: 2846; Percent complete: 71.2%; Average loss: 2.9003
Iteration: 2847; Percent complete: 71.2%; Average loss: 3.0651
Iteration: 2848; Percent complete: 71.2%; Average loss: 3.3035
Iteration: 2849; Percent complete: 71.2%; Average loss: 3.0778
Iteration: 2850; Percent complete: 71.2%; Average loss: 2.8299
Iteration: 2851; Percent complete: 71.3%; Average loss: 3.0880
Iteration: 2852; Percent complete: 71.3%; Average loss: 2.8543
Iteration: 2853; Percent complete: 71.3%; Average loss: 2.9759
Iteration: 2854; Percent complete: 71.4%; Average loss: 2.9948
Iteration: 2855; Percent complete: 71.4%; Average loss: 2.9255
Iteration: 2856; Percent complete: 71.4%; Average loss: 2.6577
Iteration: 2857; Percent complete: 71.4%; Average loss: 3.0969
Iteration: 2858; Percent complete: 71.5%; Average loss: 2.9127
Iteration: 2859; Percent complete: 71.5%; Average loss: 3.0904
Iteration: 2860; Percent complete: 71.5%; Average loss: 3.0594
Iteration: 2861; Percent complete: 71.5%; Average loss: 2.8319
Iteration: 2862; Percent complete: 71.5%; Average loss: 2.9565
Iteration: 2863; Percent complete: 71.6%; Average loss: 2.6427
Iteration: 2864; Percent complete: 71.6%; Average loss: 2.9436
Iteration: 2865; Percent complete: 71.6%; Average loss: 2.9872
Iteration: 2866; Percent complete: 71.7%; Average loss: 3.1768
Iteration: 2867; Percent complete: 71.7%; Average loss: 2.6414
Iteration: 2868; Percent complete: 71.7%; Average loss: 2.9805
Iteration: 2869; Percent complete: 71.7%; Average loss: 2.6962
Iteration: 2870; Percent complete: 71.8%; Average loss: 2.8833
Iteration: 2871; Percent complete: 71.8%; Average loss: 2.8438
Iteration: 2872; Percent complete: 71.8%; Average loss: 2.6726
Iteration: 2873; Percent complete: 71.8%; Average loss: 2.9369
Iteration: 2874; Percent complete: 71.9%; Average loss: 2.9936
Iteration: 2875; Percent complete: 71.9%; Average loss: 2.9046
Iteration: 2876; Percent complete: 71.9%; Average loss: 2.9971
Iteration: 2877; Percent complete: 71.9%; Average loss: 2.7360
Iteration: 2878; Percent complete: 72.0%; Average loss: 3.1189
Iteration: 2879; Percent complete: 72.0%; Average loss: 2.8965
Iteration: 2880; Percent complete: 72.0%; Average loss: 3.0444
Iteration: 2881; Percent complete: 72.0%; Average loss: 2.7687
Iteration: 2882; Percent complete: 72.0%; Average loss: 2.8867
Iteration: 2883; Percent complete: 72.1%; Average loss: 2.9289
Iteration: 2884; Percent complete: 72.1%; Average loss: 2.7020
Iteration: 2885; Percent complete: 72.1%; Average loss: 2.9859
Iteration: 2886; Percent complete: 72.2%; Average loss: 3.1801
Iteration: 2887; Percent complete: 72.2%; Average loss: 2.7313
Iteration: 2888; Percent complete: 72.2%; Average loss: 2.6717
Iteration: 2889; Percent complete: 72.2%; Average loss: 3.0081
Iteration: 2890; Percent complete: 72.2%; Average loss: 2.8106
Iteration: 2891; Percent complete: 72.3%; Average loss: 2.9287
Iteration: 2892; Percent complete: 72.3%; Average loss: 2.8350
Iteration: 2893; Percent complete: 72.3%; Average loss: 3.0611
Iteration: 2894; Percent complete: 72.4%; Average loss: 2.9588
Iteration: 2895; Percent complete: 72.4%; Average loss: 3.0682
Iteration: 2896; Percent complete: 72.4%; Average loss: 3.0256
Iteration: 2897; Percent complete: 72.4%; Average loss: 3.0679
Iteration: 2898; Percent complete: 72.5%; Average loss: 2.9078
Iteration: 2899; Percent complete: 72.5%; Average loss: 2.8517
Iteration: 2900; Percent complete: 72.5%; Average loss: 2.6352
Iteration: 2901; Percent complete: 72.5%; Average loss: 2.9865
Iteration: 2902; Percent complete: 72.5%; Average loss: 2.8514
Iteration: 2903; Percent complete: 72.6%; Average loss: 3.0534
Iteration: 2904; Percent complete: 72.6%; Average loss: 2.8716
Iteration: 2905; Percent complete: 72.6%; Average loss: 2.8220
Iteration: 2906; Percent complete: 72.7%; Average loss: 2.8883
Iteration: 2907; Percent complete: 72.7%; Average loss: 2.8780
Iteration: 2908; Percent complete: 72.7%; Average loss: 2.7046
Iteration: 2909; Percent complete: 72.7%; Average loss: 3.0089
Iteration: 2910; Percent complete: 72.8%; Average loss: 3.0452
Iteration: 2911; Percent complete: 72.8%; Average loss: 2.9386
Iteration: 2912; Percent complete: 72.8%; Average loss: 2.7918
Iteration: 2913; Percent complete: 72.8%; Average loss: 2.9946
Iteration: 2914; Percent complete: 72.9%; Average loss: 2.9328
Iteration: 2915; Percent complete: 72.9%; Average loss: 2.8748
Iteration: 2916; Percent complete: 72.9%; Average loss: 2.7918
Iteration: 2917; Percent complete: 72.9%; Average loss: 2.7235
Iteration: 2918; Percent complete: 73.0%; Average loss: 2.8356
Iteration: 2919; Percent complete: 73.0%; Average loss: 2.9148
Iteration: 2920; Percent complete: 73.0%; Average loss: 2.8983
Iteration: 2921; Percent complete: 73.0%; Average loss: 2.6429
Iteration: 2922; Percent complete: 73.0%; Average loss: 2.6313
Iteration: 2923; Percent complete: 73.1%; Average loss: 3.0211
Iteration: 2924; Percent complete: 73.1%; Average loss: 2.8429
Iteration: 2925; Percent complete: 73.1%; Average loss: 3.1007
Iteration: 2926; Percent complete: 73.2%; Average loss: 2.9678
Iteration: 2927; Percent complete: 73.2%; Average loss: 2.9266
Iteration: 2928; Percent complete: 73.2%; Average loss: 2.9993
Iteration: 2929; Percent complete: 73.2%; Average loss: 2.8836
Iteration: 2930; Percent complete: 73.2%; Average loss: 2.7586
Iteration: 2931; Percent complete: 73.3%; Average loss: 2.9192
Iteration: 2932; Percent complete: 73.3%; Average loss: 2.7213
Iteration: 2933; Percent complete: 73.3%; Average loss: 2.7638
Iteration: 2934; Percent complete: 73.4%; Average loss: 2.9432
Iteration: 2935; Percent complete: 73.4%; Average loss: 2.9714
Iteration: 2936; Percent complete: 73.4%; Average loss: 2.8404
Iteration: 2937; Percent complete: 73.4%; Average loss: 2.7766
Iteration: 2938; Percent complete: 73.5%; Average loss: 2.9330
Iteration: 2939; Percent complete: 73.5%; Average loss: 2.9222
Iteration: 2940; Percent complete: 73.5%; Average loss: 2.8148
Iteration: 2941; Percent complete: 73.5%; Average loss: 2.7697
Iteration: 2942; Percent complete: 73.6%; Average loss: 2.7128
Iteration: 2943; Percent complete: 73.6%; Average loss: 2.9312
Iteration: 2944; Percent complete: 73.6%; Average loss: 2.7968
Iteration: 2945; Percent complete: 73.6%; Average loss: 2.6992
Iteration: 2946; Percent complete: 73.7%; Average loss: 2.8884
Iteration: 2947; Percent complete: 73.7%; Average loss: 2.8413
Iteration: 2948; Percent complete: 73.7%; Average loss: 3.0453
Iteration: 2949; Percent complete: 73.7%; Average loss: 2.8239
Iteration: 2950; Percent complete: 73.8%; Average loss: 2.8382
Iteration: 2951; Percent complete: 73.8%; Average loss: 2.8630
Iteration: 2952; Percent complete: 73.8%; Average loss: 2.8599
Iteration: 2953; Percent complete: 73.8%; Average loss: 2.9015
Iteration: 2954; Percent complete: 73.9%; Average loss: 2.7042
Iteration: 2955; Percent complete: 73.9%; Average loss: 2.8568
Iteration: 2956; Percent complete: 73.9%; Average loss: 2.9037
Iteration: 2957; Percent complete: 73.9%; Average loss: 2.8384
Iteration: 2958; Percent complete: 74.0%; Average loss: 2.7465
Iteration: 2959; Percent complete: 74.0%; Average loss: 2.7712
Iteration: 2960; Percent complete: 74.0%; Average loss: 3.0023
Iteration: 2961; Percent complete: 74.0%; Average loss: 2.7576
Iteration: 2962; Percent complete: 74.1%; Average loss: 2.8271
Iteration: 2963; Percent complete: 74.1%; Average loss: 2.8618
Iteration: 2964; Percent complete: 74.1%; Average loss: 2.8559
Iteration: 2965; Percent complete: 74.1%; Average loss: 2.9354
Iteration: 2966; Percent complete: 74.2%; Average loss: 3.0062
Iteration: 2967; Percent complete: 74.2%; Average loss: 2.9835
Iteration: 2968; Percent complete: 74.2%; Average loss: 2.8867
Iteration: 2969; Percent complete: 74.2%; Average loss: 2.7094
Iteration: 2970; Percent complete: 74.2%; Average loss: 2.7304
Iteration: 2971; Percent complete: 74.3%; Average loss: 2.6626
Iteration: 2972; Percent complete: 74.3%; Average loss: 2.7568
Iteration: 2973; Percent complete: 74.3%; Average loss: 2.7110
Iteration: 2974; Percent complete: 74.4%; Average loss: 2.9368
Iteration: 2975; Percent complete: 74.4%; Average loss: 2.7589
Iteration: 2976; Percent complete: 74.4%; Average loss: 3.0386
Iteration: 2977; Percent complete: 74.4%; Average loss: 2.7655
Iteration: 2978; Percent complete: 74.5%; Average loss: 2.8056
Iteration: 2979; Percent complete: 74.5%; Average loss: 2.9610
Iteration: 2980; Percent complete: 74.5%; Average loss: 2.9284
Iteration: 2981; Percent complete: 74.5%; Average loss: 2.6354
Iteration: 2982; Percent complete: 74.6%; Average loss: 2.9493
Iteration: 2983; Percent complete: 74.6%; Average loss: 3.0044
Iteration: 2984; Percent complete: 74.6%; Average loss: 2.9814
Iteration: 2985; Percent complete: 74.6%; Average loss: 2.8239
Iteration: 2986; Percent complete: 74.7%; Average loss: 2.9033
Iteration: 2987; Percent complete: 74.7%; Average loss: 2.7374
Iteration: 2988; Percent complete: 74.7%; Average loss: 2.8227
Iteration: 2989; Percent complete: 74.7%; Average loss: 2.7802
Iteration: 2990; Percent complete: 74.8%; Average loss: 3.0992
Iteration: 2991; Percent complete: 74.8%; Average loss: 3.1458
Iteration: 2992; Percent complete: 74.8%; Average loss: 2.7283
Iteration: 2993; Percent complete: 74.8%; Average loss: 2.9385
Iteration: 2994; Percent complete: 74.9%; Average loss: 2.9148
Iteration: 2995; Percent complete: 74.9%; Average loss: 2.7577
Iteration: 2996; Percent complete: 74.9%; Average loss: 3.0144
Iteration: 2997; Percent complete: 74.9%; Average loss: 2.7879
Iteration: 2998; Percent complete: 75.0%; Average loss: 2.8962
Iteration: 2999; Percent complete: 75.0%; Average loss: 2.9533
Iteration: 3000; Percent complete: 75.0%; Average loss: 2.7649
Iteration: 3001; Percent complete: 75.0%; Average loss: 3.1234
Iteration: 3002; Percent complete: 75.0%; Average loss: 2.8810
Iteration: 3003; Percent complete: 75.1%; Average loss: 2.8531
Iteration: 3004; Percent complete: 75.1%; Average loss: 2.9274
Iteration: 3005; Percent complete: 75.1%; Average loss: 3.0255
Iteration: 3006; Percent complete: 75.1%; Average loss: 3.1106
Iteration: 3007; Percent complete: 75.2%; Average loss: 2.7965
Iteration: 3008; Percent complete: 75.2%; Average loss: 2.7921
Iteration: 3009; Percent complete: 75.2%; Average loss: 2.9918
Iteration: 3010; Percent complete: 75.2%; Average loss: 2.6828
Iteration: 3011; Percent complete: 75.3%; Average loss: 2.9174
Iteration: 3012; Percent complete: 75.3%; Average loss: 2.9853
Iteration: 3013; Percent complete: 75.3%; Average loss: 2.8277
Iteration: 3014; Percent complete: 75.3%; Average loss: 2.8702
Iteration: 3015; Percent complete: 75.4%; Average loss: 2.8930
Iteration: 3016; Percent complete: 75.4%; Average loss: 2.8959
Iteration: 3017; Percent complete: 75.4%; Average loss: 2.9706
Iteration: 3018; Percent complete: 75.4%; Average loss: 3.1190
Iteration: 3019; Percent complete: 75.5%; Average loss: 2.7280
Iteration: 3020; Percent complete: 75.5%; Average loss: 2.6583
Iteration: 3021; Percent complete: 75.5%; Average loss: 2.9079
Iteration: 3022; Percent complete: 75.5%; Average loss: 2.8317
Iteration: 3023; Percent complete: 75.6%; Average loss: 3.0108
Iteration: 3024; Percent complete: 75.6%; Average loss: 3.0968
Iteration: 3025; Percent complete: 75.6%; Average loss: 2.8549
Iteration: 3026; Percent complete: 75.6%; Average loss: 2.9425
Iteration: 3027; Percent complete: 75.7%; Average loss: 2.9209
Iteration: 3028; Percent complete: 75.7%; Average loss: 2.7472
Iteration: 3029; Percent complete: 75.7%; Average loss: 2.8500
Iteration: 3030; Percent complete: 75.8%; Average loss: 2.7146
Iteration: 3031; Percent complete: 75.8%; Average loss: 2.7995
Iteration: 3032; Percent complete: 75.8%; Average loss: 2.9801
Iteration: 3033; Percent complete: 75.8%; Average loss: 2.7764
Iteration: 3034; Percent complete: 75.8%; Average loss: 2.9251
Iteration: 3035; Percent complete: 75.9%; Average loss: 2.7050
Iteration: 3036; Percent complete: 75.9%; Average loss: 2.6465
Iteration: 3037; Percent complete: 75.9%; Average loss: 3.0059
Iteration: 3038; Percent complete: 75.9%; Average loss: 2.5441
Iteration: 3039; Percent complete: 76.0%; Average loss: 2.9330
Iteration: 3040; Percent complete: 76.0%; Average loss: 2.7263
Iteration: 3041; Percent complete: 76.0%; Average loss: 2.8928
Iteration: 3042; Percent complete: 76.0%; Average loss: 2.7641
Iteration: 3043; Percent complete: 76.1%; Average loss: 2.7620
Iteration: 3044; Percent complete: 76.1%; Average loss: 3.0987
Iteration: 3045; Percent complete: 76.1%; Average loss: 3.0335
Iteration: 3046; Percent complete: 76.1%; Average loss: 3.1407
Iteration: 3047; Percent complete: 76.2%; Average loss: 2.7664
Iteration: 3048; Percent complete: 76.2%; Average loss: 2.5986
Iteration: 3049; Percent complete: 76.2%; Average loss: 3.1426
Iteration: 3050; Percent complete: 76.2%; Average loss: 3.0746
Iteration: 3051; Percent complete: 76.3%; Average loss: 3.1142
Iteration: 3052; Percent complete: 76.3%; Average loss: 2.7600
Iteration: 3053; Percent complete: 76.3%; Average loss: 2.9727
Iteration: 3054; Percent complete: 76.3%; Average loss: 2.8641
Iteration: 3055; Percent complete: 76.4%; Average loss: 2.7927
Iteration: 3056; Percent complete: 76.4%; Average loss: 3.1077
Iteration: 3057; Percent complete: 76.4%; Average loss: 2.9872
Iteration: 3058; Percent complete: 76.4%; Average loss: 2.8404
Iteration: 3059; Percent complete: 76.5%; Average loss: 2.8024
Iteration: 3060; Percent complete: 76.5%; Average loss: 2.6718
Iteration: 3061; Percent complete: 76.5%; Average loss: 3.0057
Iteration: 3062; Percent complete: 76.5%; Average loss: 2.8620
Iteration: 3063; Percent complete: 76.6%; Average loss: 2.8365
Iteration: 3064; Percent complete: 76.6%; Average loss: 2.8264
Iteration: 3065; Percent complete: 76.6%; Average loss: 2.8181
Iteration: 3066; Percent complete: 76.6%; Average loss: 2.8484
Iteration: 3067; Percent complete: 76.7%; Average loss: 2.8804
Iteration: 3068; Percent complete: 76.7%; Average loss: 2.8627
Iteration: 3069; Percent complete: 76.7%; Average loss: 2.7562
Iteration: 3070; Percent complete: 76.8%; Average loss: 2.8148
Iteration: 3071; Percent complete: 76.8%; Average loss: 2.7640
Iteration: 3072; Percent complete: 76.8%; Average loss: 3.1099
Iteration: 3073; Percent complete: 76.8%; Average loss: 3.0060
Iteration: 3074; Percent complete: 76.8%; Average loss: 2.7516
Iteration: 3075; Percent complete: 76.9%; Average loss: 2.9093
Iteration: 3076; Percent complete: 76.9%; Average loss: 2.7393
Iteration: 3077; Percent complete: 76.9%; Average loss: 2.7853
Iteration: 3078; Percent complete: 77.0%; Average loss: 2.8812
Iteration: 3079; Percent complete: 77.0%; Average loss: 2.9951
Iteration: 3080; Percent complete: 77.0%; Average loss: 2.8363
Iteration: 3081; Percent complete: 77.0%; Average loss: 3.0091
Iteration: 3082; Percent complete: 77.0%; Average loss: 2.6011
Iteration: 3083; Percent complete: 77.1%; Average loss: 3.0179
Iteration: 3084; Percent complete: 77.1%; Average loss: 3.0152
Iteration: 3085; Percent complete: 77.1%; Average loss: 2.9442
Iteration: 3086; Percent complete: 77.1%; Average loss: 2.8225
Iteration: 3087; Percent complete: 77.2%; Average loss: 2.8828
Iteration: 3088; Percent complete: 77.2%; Average loss: 2.8883
Iteration: 3089; Percent complete: 77.2%; Average loss: 2.7517
Iteration: 3090; Percent complete: 77.2%; Average loss: 2.7943
Iteration: 3091; Percent complete: 77.3%; Average loss: 2.7993
Iteration: 3092; Percent complete: 77.3%; Average loss: 2.6965
Iteration: 3093; Percent complete: 77.3%; Average loss: 2.9222
Iteration: 3094; Percent complete: 77.3%; Average loss: 2.6321
Iteration: 3095; Percent complete: 77.4%; Average loss: 2.8029
Iteration: 3096; Percent complete: 77.4%; Average loss: 2.7811
Iteration: 3097; Percent complete: 77.4%; Average loss: 2.7555
Iteration: 3098; Percent complete: 77.5%; Average loss: 2.9072
Iteration: 3099; Percent complete: 77.5%; Average loss: 2.6939
Iteration: 3100; Percent complete: 77.5%; Average loss: 2.9542
Iteration: 3101; Percent complete: 77.5%; Average loss: 2.6258
Iteration: 3102; Percent complete: 77.5%; Average loss: 2.8355
Iteration: 3103; Percent complete: 77.6%; Average loss: 2.7703
Iteration: 3104; Percent complete: 77.6%; Average loss: 2.8207
Iteration: 3105; Percent complete: 77.6%; Average loss: 3.0199
Iteration: 3106; Percent complete: 77.6%; Average loss: 3.1022
Iteration: 3107; Percent complete: 77.7%; Average loss: 2.8323
Iteration: 3108; Percent complete: 77.7%; Average loss: 2.6988
Iteration: 3109; Percent complete: 77.7%; Average loss: 3.0627
Iteration: 3110; Percent complete: 77.8%; Average loss: 2.7438
Iteration: 3111; Percent complete: 77.8%; Average loss: 2.7882
Iteration: 3112; Percent complete: 77.8%; Average loss: 3.0288
Iteration: 3113; Percent complete: 77.8%; Average loss: 3.0389
Iteration: 3114; Percent complete: 77.8%; Average loss: 2.8933
Iteration: 3115; Percent complete: 77.9%; Average loss: 2.9403
Iteration: 3116; Percent complete: 77.9%; Average loss: 2.8903
Iteration: 3117; Percent complete: 77.9%; Average loss: 2.8931
Iteration: 3118; Percent complete: 78.0%; Average loss: 2.8295
Iteration: 3119; Percent complete: 78.0%; Average loss: 2.8142
Iteration: 3120; Percent complete: 78.0%; Average loss: 3.1177
Iteration: 3121; Percent complete: 78.0%; Average loss: 2.9038
Iteration: 3122; Percent complete: 78.0%; Average loss: 2.9016
Iteration: 3123; Percent complete: 78.1%; Average loss: 2.6159
Iteration: 3124; Percent complete: 78.1%; Average loss: 2.9701
Iteration: 3125; Percent complete: 78.1%; Average loss: 2.9096
Iteration: 3126; Percent complete: 78.1%; Average loss: 2.9453
Iteration: 3127; Percent complete: 78.2%; Average loss: 2.5911
Iteration: 3128; Percent complete: 78.2%; Average loss: 2.8974
Iteration: 3129; Percent complete: 78.2%; Average loss: 2.7675
Iteration: 3130; Percent complete: 78.2%; Average loss: 3.0036
Iteration: 3131; Percent complete: 78.3%; Average loss: 2.8504
Iteration: 3132; Percent complete: 78.3%; Average loss: 2.7229
Iteration: 3133; Percent complete: 78.3%; Average loss: 2.6590
Iteration: 3134; Percent complete: 78.3%; Average loss: 2.8910
Iteration: 3135; Percent complete: 78.4%; Average loss: 2.6893
Iteration: 3136; Percent complete: 78.4%; Average loss: 2.5640
Iteration: 3137; Percent complete: 78.4%; Average loss: 2.8659
Iteration: 3138; Percent complete: 78.5%; Average loss: 2.9104
Iteration: 3139; Percent complete: 78.5%; Average loss: 2.8004
Iteration: 3140; Percent complete: 78.5%; Average loss: 2.9165
Iteration: 3141; Percent complete: 78.5%; Average loss: 2.7353
Iteration: 3142; Percent complete: 78.5%; Average loss: 2.6800
Iteration: 3143; Percent complete: 78.6%; Average loss: 2.7219
Iteration: 3144; Percent complete: 78.6%; Average loss: 2.9591
Iteration: 3145; Percent complete: 78.6%; Average loss: 2.8603
Iteration: 3146; Percent complete: 78.6%; Average loss: 3.0224
Iteration: 3147; Percent complete: 78.7%; Average loss: 2.8053
Iteration: 3148; Percent complete: 78.7%; Average loss: 2.8767
Iteration: 3149; Percent complete: 78.7%; Average loss: 2.7098
Iteration: 3150; Percent complete: 78.8%; Average loss: 2.8971
Iteration: 3151; Percent complete: 78.8%; Average loss: 2.9215
Iteration: 3152; Percent complete: 78.8%; Average loss: 2.9266
Iteration: 3153; Percent complete: 78.8%; Average loss: 2.8404
Iteration: 3154; Percent complete: 78.8%; Average loss: 2.9506
Iteration: 3155; Percent complete: 78.9%; Average loss: 2.7518
Iteration: 3156; Percent complete: 78.9%; Average loss: 2.7396
Iteration: 3157; Percent complete: 78.9%; Average loss: 3.1016
Iteration: 3158; Percent complete: 79.0%; Average loss: 2.5426
Iteration: 3159; Percent complete: 79.0%; Average loss: 2.9394
Iteration: 3160; Percent complete: 79.0%; Average loss: 2.7314
Iteration: 3161; Percent complete: 79.0%; Average loss: 2.8191
Iteration: 3162; Percent complete: 79.0%; Average loss: 3.3064
Iteration: 3163; Percent complete: 79.1%; Average loss: 2.9101
Iteration: 3164; Percent complete: 79.1%; Average loss: 2.6968
Iteration: 3165; Percent complete: 79.1%; Average loss: 2.7107
Iteration: 3166; Percent complete: 79.1%; Average loss: 2.9214
Iteration: 3167; Percent complete: 79.2%; Average loss: 2.7449
Iteration: 3168; Percent complete: 79.2%; Average loss: 2.5854
Iteration: 3169; Percent complete: 79.2%; Average loss: 2.7822
Iteration: 3170; Percent complete: 79.2%; Average loss: 2.8382
Iteration: 3171; Percent complete: 79.3%; Average loss: 2.8617
Iteration: 3172; Percent complete: 79.3%; Average loss: 2.8009
Iteration: 3173; Percent complete: 79.3%; Average loss: 2.7498
Iteration: 3174; Percent complete: 79.3%; Average loss: 2.5740
Iteration: 3175; Percent complete: 79.4%; Average loss: 2.7993
Iteration: 3176; Percent complete: 79.4%; Average loss: 2.9701
Iteration: 3177; Percent complete: 79.4%; Average loss: 2.7760
Iteration: 3178; Percent complete: 79.5%; Average loss: 2.8316
Iteration: 3179; Percent complete: 79.5%; Average loss: 2.7745
Iteration: 3180; Percent complete: 79.5%; Average loss: 3.0121
Iteration: 3181; Percent complete: 79.5%; Average loss: 2.6680
Iteration: 3182; Percent complete: 79.5%; Average loss: 2.8994
Iteration: 3183; Percent complete: 79.6%; Average loss: 3.0193
Iteration: 3184; Percent complete: 79.6%; Average loss: 2.7518
Iteration: 3185; Percent complete: 79.6%; Average loss: 2.8548
Iteration: 3186; Percent complete: 79.7%; Average loss: 3.0379
Iteration: 3187; Percent complete: 79.7%; Average loss: 2.8878
Iteration: 3188; Percent complete: 79.7%; Average loss: 2.7285
Iteration: 3189; Percent complete: 79.7%; Average loss: 2.9408
Iteration: 3190; Percent complete: 79.8%; Average loss: 2.8778
Iteration: 3191; Percent complete: 79.8%; Average loss: 2.7097
Iteration: 3192; Percent complete: 79.8%; Average loss: 2.9021
Iteration: 3193; Percent complete: 79.8%; Average loss: 2.6743
Iteration: 3194; Percent complete: 79.8%; Average loss: 2.8463
Iteration: 3195; Percent complete: 79.9%; Average loss: 2.8095
Iteration: 3196; Percent complete: 79.9%; Average loss: 2.8497
Iteration: 3197; Percent complete: 79.9%; Average loss: 2.9991
Iteration: 3198; Percent complete: 80.0%; Average loss: 2.7953
Iteration: 3199; Percent complete: 80.0%; Average loss: 2.6491
Iteration: 3200; Percent complete: 80.0%; Average loss: 2.6459
Iteration: 3201; Percent complete: 80.0%; Average loss: 2.9211
Iteration: 3202; Percent complete: 80.0%; Average loss: 2.9348
Iteration: 3203; Percent complete: 80.1%; Average loss: 2.7201
Iteration: 3204; Percent complete: 80.1%; Average loss: 3.1622
Iteration: 3205; Percent complete: 80.1%; Average loss: 2.7457
Iteration: 3206; Percent complete: 80.2%; Average loss: 2.8959
Iteration: 3207; Percent complete: 80.2%; Average loss: 2.8990
Iteration: 3208; Percent complete: 80.2%; Average loss: 2.6221
Iteration: 3209; Percent complete: 80.2%; Average loss: 2.8573
Iteration: 3210; Percent complete: 80.2%; Average loss: 2.7068
Iteration: 3211; Percent complete: 80.3%; Average loss: 2.8311
Iteration: 3212; Percent complete: 80.3%; Average loss: 2.5822
Iteration: 3213; Percent complete: 80.3%; Average loss: 2.9463
Iteration: 3214; Percent complete: 80.3%; Average loss: 2.5307
Iteration: 3215; Percent complete: 80.4%; Average loss: 2.8870
Iteration: 3216; Percent complete: 80.4%; Average loss: 2.7281
Iteration: 3217; Percent complete: 80.4%; Average loss: 2.6097
Iteration: 3218; Percent complete: 80.5%; Average loss: 2.8158
Iteration: 3219; Percent complete: 80.5%; Average loss: 2.8780
Iteration: 3220; Percent complete: 80.5%; Average loss: 2.4754
Iteration: 3221; Percent complete: 80.5%; Average loss: 2.7519
Iteration: 3222; Percent complete: 80.5%; Average loss: 2.9663
Iteration: 3223; Percent complete: 80.6%; Average loss: 2.7549
Iteration: 3224; Percent complete: 80.6%; Average loss: 2.7535
Iteration: 3225; Percent complete: 80.6%; Average loss: 2.5724
Iteration: 3226; Percent complete: 80.7%; Average loss: 2.7303
Iteration: 3227; Percent complete: 80.7%; Average loss: 2.6351
Iteration: 3228; Percent complete: 80.7%; Average loss: 2.9577
Iteration: 3229; Percent complete: 80.7%; Average loss: 2.6565
Iteration: 3230; Percent complete: 80.8%; Average loss: 2.8309
Iteration: 3231; Percent complete: 80.8%; Average loss: 2.8662
Iteration: 3232; Percent complete: 80.8%; Average loss: 2.9646
Iteration: 3233; Percent complete: 80.8%; Average loss: 3.0701
Iteration: 3234; Percent complete: 80.8%; Average loss: 2.8108
Iteration: 3235; Percent complete: 80.9%; Average loss: 3.1464
Iteration: 3236; Percent complete: 80.9%; Average loss: 2.8162
Iteration: 3237; Percent complete: 80.9%; Average loss: 2.8089
Iteration: 3238; Percent complete: 81.0%; Average loss: 2.9906
Iteration: 3239; Percent complete: 81.0%; Average loss: 2.9472
Iteration: 3240; Percent complete: 81.0%; Average loss: 2.7888
Iteration: 3241; Percent complete: 81.0%; Average loss: 2.8156
Iteration: 3242; Percent complete: 81.0%; Average loss: 2.8915
Iteration: 3243; Percent complete: 81.1%; Average loss: 2.9195
Iteration: 3244; Percent complete: 81.1%; Average loss: 2.7711
Iteration: 3245; Percent complete: 81.1%; Average loss: 2.7468
Iteration: 3246; Percent complete: 81.2%; Average loss: 2.6339
Iteration: 3247; Percent complete: 81.2%; Average loss: 3.0075
Iteration: 3248; Percent complete: 81.2%; Average loss: 2.6950
Iteration: 3249; Percent complete: 81.2%; Average loss: 2.8205
Iteration: 3250; Percent complete: 81.2%; Average loss: 2.8571
Iteration: 3251; Percent complete: 81.3%; Average loss: 2.5403
Iteration: 3252; Percent complete: 81.3%; Average loss: 2.7048
Iteration: 3253; Percent complete: 81.3%; Average loss: 2.9637
Iteration: 3254; Percent complete: 81.3%; Average loss: 2.8883
Iteration: 3255; Percent complete: 81.4%; Average loss: 2.7152
Iteration: 3256; Percent complete: 81.4%; Average loss: 2.6304
Iteration: 3257; Percent complete: 81.4%; Average loss: 2.7526
Iteration: 3258; Percent complete: 81.5%; Average loss: 2.8955
Iteration: 3259; Percent complete: 81.5%; Average loss: 2.9132
Iteration: 3260; Percent complete: 81.5%; Average loss: 2.6679
Iteration: 3261; Percent complete: 81.5%; Average loss: 2.7017
Iteration: 3262; Percent complete: 81.5%; Average loss: 3.1152
Iteration: 3263; Percent complete: 81.6%; Average loss: 2.7892
Iteration: 3264; Percent complete: 81.6%; Average loss: 2.7845
Iteration: 3265; Percent complete: 81.6%; Average loss: 2.8792
Iteration: 3266; Percent complete: 81.7%; Average loss: 2.7737
Iteration: 3267; Percent complete: 81.7%; Average loss: 2.6896
Iteration: 3268; Percent complete: 81.7%; Average loss: 2.6371
Iteration: 3269; Percent complete: 81.7%; Average loss: 2.8589
Iteration: 3270; Percent complete: 81.8%; Average loss: 2.9549
Iteration: 3271; Percent complete: 81.8%; Average loss: 3.1036
Iteration: 3272; Percent complete: 81.8%; Average loss: 2.6430
Iteration: 3273; Percent complete: 81.8%; Average loss: 2.7658
Iteration: 3274; Percent complete: 81.8%; Average loss: 2.7043
Iteration: 3275; Percent complete: 81.9%; Average loss: 2.7454
Iteration: 3276; Percent complete: 81.9%; Average loss: 2.8132
Iteration: 3277; Percent complete: 81.9%; Average loss: 2.7993
Iteration: 3278; Percent complete: 82.0%; Average loss: 2.8330
Iteration: 3279; Percent complete: 82.0%; Average loss: 3.0938
Iteration: 3280; Percent complete: 82.0%; Average loss: 2.8563
Iteration: 3281; Percent complete: 82.0%; Average loss: 2.7569
Iteration: 3282; Percent complete: 82.0%; Average loss: 2.6975
Iteration: 3283; Percent complete: 82.1%; Average loss: 2.6856
Iteration: 3284; Percent complete: 82.1%; Average loss: 2.7037
Iteration: 3285; Percent complete: 82.1%; Average loss: 2.7571
Iteration: 3286; Percent complete: 82.2%; Average loss: 2.8480
Iteration: 3287; Percent complete: 82.2%; Average loss: 2.9901
Iteration: 3288; Percent complete: 82.2%; Average loss: 2.9056
Iteration: 3289; Percent complete: 82.2%; Average loss: 2.8657
Iteration: 3290; Percent complete: 82.2%; Average loss: 2.7261
Iteration: 3291; Percent complete: 82.3%; Average loss: 2.7198
Iteration: 3292; Percent complete: 82.3%; Average loss: 2.7939
Iteration: 3293; Percent complete: 82.3%; Average loss: 2.8440
Iteration: 3294; Percent complete: 82.3%; Average loss: 2.7509
Iteration: 3295; Percent complete: 82.4%; Average loss: 2.6429
Iteration: 3296; Percent complete: 82.4%; Average loss: 2.6369
Iteration: 3297; Percent complete: 82.4%; Average loss: 2.7131
Iteration: 3298; Percent complete: 82.5%; Average loss: 2.8859
Iteration: 3299; Percent complete: 82.5%; Average loss: 2.7440
Iteration: 3300; Percent complete: 82.5%; Average loss: 2.7228
Iteration: 3301; Percent complete: 82.5%; Average loss: 2.6256
Iteration: 3302; Percent complete: 82.5%; Average loss: 2.9388
Iteration: 3303; Percent complete: 82.6%; Average loss: 2.5489
Iteration: 3304; Percent complete: 82.6%; Average loss: 2.9164
Iteration: 3305; Percent complete: 82.6%; Average loss: 3.0635
Iteration: 3306; Percent complete: 82.7%; Average loss: 2.9431
Iteration: 3307; Percent complete: 82.7%; Average loss: 2.8945
Iteration: 3308; Percent complete: 82.7%; Average loss: 2.6491
Iteration: 3309; Percent complete: 82.7%; Average loss: 2.8680
Iteration: 3310; Percent complete: 82.8%; Average loss: 2.5462
Iteration: 3311; Percent complete: 82.8%; Average loss: 2.7202
Iteration: 3312; Percent complete: 82.8%; Average loss: 2.8828
Iteration: 3313; Percent complete: 82.8%; Average loss: 2.7953
Iteration: 3314; Percent complete: 82.8%; Average loss: 2.7665
Iteration: 3315; Percent complete: 82.9%; Average loss: 2.7617
Iteration: 3316; Percent complete: 82.9%; Average loss: 2.8865
Iteration: 3317; Percent complete: 82.9%; Average loss: 2.7883
Iteration: 3318; Percent complete: 83.0%; Average loss: 2.8164
Iteration: 3319; Percent complete: 83.0%; Average loss: 2.6106
Iteration: 3320; Percent complete: 83.0%; Average loss: 2.6027
Iteration: 3321; Percent complete: 83.0%; Average loss: 2.9996
Iteration: 3322; Percent complete: 83.0%; Average loss: 2.8621
Iteration: 3323; Percent complete: 83.1%; Average loss: 2.9844
Iteration: 3324; Percent complete: 83.1%; Average loss: 2.8555
Iteration: 3325; Percent complete: 83.1%; Average loss: 2.6969
Iteration: 3326; Percent complete: 83.2%; Average loss: 2.7708
Iteration: 3327; Percent complete: 83.2%; Average loss: 2.7832
Iteration: 3328; Percent complete: 83.2%; Average loss: 2.7835
Iteration: 3329; Percent complete: 83.2%; Average loss: 2.6768
Iteration: 3330; Percent complete: 83.2%; Average loss: 2.9622
Iteration: 3331; Percent complete: 83.3%; Average loss: 2.9145
Iteration: 3332; Percent complete: 83.3%; Average loss: 2.7083
Iteration: 3333; Percent complete: 83.3%; Average loss: 2.9200
Iteration: 3334; Percent complete: 83.4%; Average loss: 3.0020
Iteration: 3335; Percent complete: 83.4%; Average loss: 2.5735
Iteration: 3336; Percent complete: 83.4%; Average loss: 2.7433
Iteration: 3337; Percent complete: 83.4%; Average loss: 2.9919
Iteration: 3338; Percent complete: 83.5%; Average loss: 2.9810
Iteration: 3339; Percent complete: 83.5%; Average loss: 2.9674
Iteration: 3340; Percent complete: 83.5%; Average loss: 2.5871
Iteration: 3341; Percent complete: 83.5%; Average loss: 2.6148
Iteration: 3342; Percent complete: 83.5%; Average loss: 2.8367
Iteration: 3343; Percent complete: 83.6%; Average loss: 2.9278
Iteration: 3344; Percent complete: 83.6%; Average loss: 2.7144
Iteration: 3345; Percent complete: 83.6%; Average loss: 2.4664
Iteration: 3346; Percent complete: 83.7%; Average loss: 2.6303
Iteration: 3347; Percent complete: 83.7%; Average loss: 2.8614
Iteration: 3348; Percent complete: 83.7%; Average loss: 2.8409
Iteration: 3349; Percent complete: 83.7%; Average loss: 2.6849
Iteration: 3350; Percent complete: 83.8%; Average loss: 2.7360
Iteration: 3351; Percent complete: 83.8%; Average loss: 2.8718
Iteration: 3352; Percent complete: 83.8%; Average loss: 2.6270
Iteration: 3353; Percent complete: 83.8%; Average loss: 2.9169
Iteration: 3354; Percent complete: 83.9%; Average loss: 2.8562
Iteration: 3355; Percent complete: 83.9%; Average loss: 2.9913
Iteration: 3356; Percent complete: 83.9%; Average loss: 2.6984
Iteration: 3357; Percent complete: 83.9%; Average loss: 2.5645
Iteration: 3358; Percent complete: 84.0%; Average loss: 2.4640
Iteration: 3359; Percent complete: 84.0%; Average loss: 2.7948
Iteration: 3360; Percent complete: 84.0%; Average loss: 2.6935
Iteration: 3361; Percent complete: 84.0%; Average loss: 2.9523
Iteration: 3362; Percent complete: 84.0%; Average loss: 2.6901
Iteration: 3363; Percent complete: 84.1%; Average loss: 2.8983
Iteration: 3364; Percent complete: 84.1%; Average loss: 2.9151
Iteration: 3365; Percent complete: 84.1%; Average loss: 2.7127
Iteration: 3366; Percent complete: 84.2%; Average loss: 2.5539
Iteration: 3367; Percent complete: 84.2%; Average loss: 2.8117
Iteration: 3368; Percent complete: 84.2%; Average loss: 2.6772
Iteration: 3369; Percent complete: 84.2%; Average loss: 2.8103
Iteration: 3370; Percent complete: 84.2%; Average loss: 2.7682
Iteration: 3371; Percent complete: 84.3%; Average loss: 2.7107
Iteration: 3372; Percent complete: 84.3%; Average loss: 2.5872
Iteration: 3373; Percent complete: 84.3%; Average loss: 2.4477
Iteration: 3374; Percent complete: 84.4%; Average loss: 3.0086
Iteration: 3375; Percent complete: 84.4%; Average loss: 2.9303
Iteration: 3376; Percent complete: 84.4%; Average loss: 2.7460
Iteration: 3377; Percent complete: 84.4%; Average loss: 2.8339
Iteration: 3378; Percent complete: 84.5%; Average loss: 2.8284
Iteration: 3379; Percent complete: 84.5%; Average loss: 3.0126
Iteration: 3380; Percent complete: 84.5%; Average loss: 2.9134
Iteration: 3381; Percent complete: 84.5%; Average loss: 2.6646
Iteration: 3382; Percent complete: 84.5%; Average loss: 2.7073
Iteration: 3383; Percent complete: 84.6%; Average loss: 2.6459
Iteration: 3384; Percent complete: 84.6%; Average loss: 2.6721
Iteration: 3385; Percent complete: 84.6%; Average loss: 2.7974
Iteration: 3386; Percent complete: 84.7%; Average loss: 2.6945
Iteration: 3387; Percent complete: 84.7%; Average loss: 2.8126
Iteration: 3388; Percent complete: 84.7%; Average loss: 2.7901
Iteration: 3389; Percent complete: 84.7%; Average loss: 2.7238
Iteration: 3390; Percent complete: 84.8%; Average loss: 2.7153
Iteration: 3391; Percent complete: 84.8%; Average loss: 2.8125
Iteration: 3392; Percent complete: 84.8%; Average loss: 2.7568
Iteration: 3393; Percent complete: 84.8%; Average loss: 2.7086
Iteration: 3394; Percent complete: 84.9%; Average loss: 2.8056
Iteration: 3395; Percent complete: 84.9%; Average loss: 2.7405
Iteration: 3396; Percent complete: 84.9%; Average loss: 2.7341
Iteration: 3397; Percent complete: 84.9%; Average loss: 2.8117
Iteration: 3398; Percent complete: 85.0%; Average loss: 2.8281
Iteration: 3399; Percent complete: 85.0%; Average loss: 2.9725
Iteration: 3400; Percent complete: 85.0%; Average loss: 2.6458
Iteration: 3401; Percent complete: 85.0%; Average loss: 2.7611
Iteration: 3402; Percent complete: 85.0%; Average loss: 2.7750
Iteration: 3403; Percent complete: 85.1%; Average loss: 2.5853
Iteration: 3404; Percent complete: 85.1%; Average loss: 3.0115
Iteration: 3405; Percent complete: 85.1%; Average loss: 2.7234
Iteration: 3406; Percent complete: 85.2%; Average loss: 2.7864
Iteration: 3407; Percent complete: 85.2%; Average loss: 2.7801
Iteration: 3408; Percent complete: 85.2%; Average loss: 2.6163
Iteration: 3409; Percent complete: 85.2%; Average loss: 2.8795
Iteration: 3410; Percent complete: 85.2%; Average loss: 2.9822
Iteration: 3411; Percent complete: 85.3%; Average loss: 2.8024
Iteration: 3412; Percent complete: 85.3%; Average loss: 2.8320
Iteration: 3413; Percent complete: 85.3%; Average loss: 2.7244
Iteration: 3414; Percent complete: 85.4%; Average loss: 2.9327
Iteration: 3415; Percent complete: 85.4%; Average loss: 2.6785
Iteration: 3416; Percent complete: 85.4%; Average loss: 2.9065
Iteration: 3417; Percent complete: 85.4%; Average loss: 2.5430
Iteration: 3418; Percent complete: 85.5%; Average loss: 3.0277
Iteration: 3419; Percent complete: 85.5%; Average loss: 2.9656
Iteration: 3420; Percent complete: 85.5%; Average loss: 2.7496
Iteration: 3421; Percent complete: 85.5%; Average loss: 2.6343
Iteration: 3422; Percent complete: 85.5%; Average loss: 2.4798
Iteration: 3423; Percent complete: 85.6%; Average loss: 2.7917
Iteration: 3424; Percent complete: 85.6%; Average loss: 2.8555
Iteration: 3425; Percent complete: 85.6%; Average loss: 2.8387
Iteration: 3426; Percent complete: 85.7%; Average loss: 3.0093
Iteration: 3427; Percent complete: 85.7%; Average loss: 2.7599
Iteration: 3428; Percent complete: 85.7%; Average loss: 2.7805
Iteration: 3429; Percent complete: 85.7%; Average loss: 2.7520
Iteration: 3430; Percent complete: 85.8%; Average loss: 2.8370
Iteration: 3431; Percent complete: 85.8%; Average loss: 2.6719
Iteration: 3432; Percent complete: 85.8%; Average loss: 2.7961
Iteration: 3433; Percent complete: 85.8%; Average loss: 2.7422
Iteration: 3434; Percent complete: 85.9%; Average loss: 2.8228
Iteration: 3435; Percent complete: 85.9%; Average loss: 2.7984
Iteration: 3436; Percent complete: 85.9%; Average loss: 2.7695
Iteration: 3437; Percent complete: 85.9%; Average loss: 2.8301
Iteration: 3438; Percent complete: 86.0%; Average loss: 2.7368
Iteration: 3439; Percent complete: 86.0%; Average loss: 2.6599
Iteration: 3440; Percent complete: 86.0%; Average loss: 2.7192
Iteration: 3441; Percent complete: 86.0%; Average loss: 2.9623
Iteration: 3442; Percent complete: 86.1%; Average loss: 2.8548
Iteration: 3443; Percent complete: 86.1%; Average loss: 2.8564
Iteration: 3444; Percent complete: 86.1%; Average loss: 2.8484
Iteration: 3445; Percent complete: 86.1%; Average loss: 2.7975
Iteration: 3446; Percent complete: 86.2%; Average loss: 2.7821
Iteration: 3447; Percent complete: 86.2%; Average loss: 2.7717
Iteration: 3448; Percent complete: 86.2%; Average loss: 2.6787
Iteration: 3449; Percent complete: 86.2%; Average loss: 2.6148
Iteration: 3450; Percent complete: 86.2%; Average loss: 2.5830
Iteration: 3451; Percent complete: 86.3%; Average loss: 3.0221
Iteration: 3452; Percent complete: 86.3%; Average loss: 2.7488
Iteration: 3453; Percent complete: 86.3%; Average loss: 2.7812
Iteration: 3454; Percent complete: 86.4%; Average loss: 2.6550
Iteration: 3455; Percent complete: 86.4%; Average loss: 2.7687
Iteration: 3456; Percent complete: 86.4%; Average loss: 2.7975
Iteration: 3457; Percent complete: 86.4%; Average loss: 2.8281
Iteration: 3458; Percent complete: 86.5%; Average loss: 2.6566
Iteration: 3459; Percent complete: 86.5%; Average loss: 2.8056
Iteration: 3460; Percent complete: 86.5%; Average loss: 2.6966
Iteration: 3461; Percent complete: 86.5%; Average loss: 2.8280
Iteration: 3462; Percent complete: 86.6%; Average loss: 2.9112
Iteration: 3463; Percent complete: 86.6%; Average loss: 2.6817
Iteration: 3464; Percent complete: 86.6%; Average loss: 2.5980
Iteration: 3465; Percent complete: 86.6%; Average loss: 2.9519
Iteration: 3466; Percent complete: 86.7%; Average loss: 2.7652
Iteration: 3467; Percent complete: 86.7%; Average loss: 2.7725
Iteration: 3468; Percent complete: 86.7%; Average loss: 2.4903
Iteration: 3469; Percent complete: 86.7%; Average loss: 2.7039
Iteration: 3470; Percent complete: 86.8%; Average loss: 2.5737
Iteration: 3471; Percent complete: 86.8%; Average loss: 3.0750
Iteration: 3472; Percent complete: 86.8%; Average loss: 2.8395
Iteration: 3473; Percent complete: 86.8%; Average loss: 2.4583
Iteration: 3474; Percent complete: 86.9%; Average loss: 2.6078
Iteration: 3475; Percent complete: 86.9%; Average loss: 2.7626
Iteration: 3476; Percent complete: 86.9%; Average loss: 2.7914
Iteration: 3477; Percent complete: 86.9%; Average loss: 2.7449
Iteration: 3478; Percent complete: 87.0%; Average loss: 2.7260
Iteration: 3479; Percent complete: 87.0%; Average loss: 2.7610
Iteration: 3480; Percent complete: 87.0%; Average loss: 2.7820
Iteration: 3481; Percent complete: 87.0%; Average loss: 2.6741
Iteration: 3482; Percent complete: 87.1%; Average loss: 2.8793
Iteration: 3483; Percent complete: 87.1%; Average loss: 2.7187
Iteration: 3484; Percent complete: 87.1%; Average loss: 2.8274
Iteration: 3485; Percent complete: 87.1%; Average loss: 2.7589
Iteration: 3486; Percent complete: 87.2%; Average loss: 2.7743
Iteration: 3487; Percent complete: 87.2%; Average loss: 2.8468
Iteration: 3488; Percent complete: 87.2%; Average loss: 3.0577
Iteration: 3489; Percent complete: 87.2%; Average loss: 2.6461
Iteration: 3490; Percent complete: 87.2%; Average loss: 2.4035
Iteration: 3491; Percent complete: 87.3%; Average loss: 2.7092
Iteration: 3492; Percent complete: 87.3%; Average loss: 2.6582
Iteration: 3493; Percent complete: 87.3%; Average loss: 2.7201
Iteration: 3494; Percent complete: 87.4%; Average loss: 2.6617
Iteration: 3495; Percent complete: 87.4%; Average loss: 2.5891
Iteration: 3496; Percent complete: 87.4%; Average loss: 2.5559
Iteration: 3497; Percent complete: 87.4%; Average loss: 2.6327
Iteration: 3498; Percent complete: 87.5%; Average loss: 2.5145
Iteration: 3499; Percent complete: 87.5%; Average loss: 2.6842
Iteration: 3500; Percent complete: 87.5%; Average loss: 2.6937
Iteration: 3501; Percent complete: 87.5%; Average loss: 2.7252
Iteration: 3502; Percent complete: 87.5%; Average loss: 2.7797
Iteration: 3503; Percent complete: 87.6%; Average loss: 2.7554
Iteration: 3504; Percent complete: 87.6%; Average loss: 2.7512
Iteration: 3505; Percent complete: 87.6%; Average loss: 2.8482
Iteration: 3506; Percent complete: 87.6%; Average loss: 2.8150
Iteration: 3507; Percent complete: 87.7%; Average loss: 2.9427
Iteration: 3508; Percent complete: 87.7%; Average loss: 2.7252
Iteration: 3509; Percent complete: 87.7%; Average loss: 2.6817
Iteration: 3510; Percent complete: 87.8%; Average loss: 2.8717
Iteration: 3511; Percent complete: 87.8%; Average loss: 2.8778
Iteration: 3512; Percent complete: 87.8%; Average loss: 2.5102
Iteration: 3513; Percent complete: 87.8%; Average loss: 2.8076
Iteration: 3514; Percent complete: 87.8%; Average loss: 2.6109
Iteration: 3515; Percent complete: 87.9%; Average loss: 2.6423
Iteration: 3516; Percent complete: 87.9%; Average loss: 2.5854
Iteration: 3517; Percent complete: 87.9%; Average loss: 2.7383
Iteration: 3518; Percent complete: 87.9%; Average loss: 2.8768
Iteration: 3519; Percent complete: 88.0%; Average loss: 2.8846
Iteration: 3520; Percent complete: 88.0%; Average loss: 2.9357
Iteration: 3521; Percent complete: 88.0%; Average loss: 2.8547
Iteration: 3522; Percent complete: 88.0%; Average loss: 3.0670
Iteration: 3523; Percent complete: 88.1%; Average loss: 2.7114
Iteration: 3524; Percent complete: 88.1%; Average loss: 2.8484
Iteration: 3525; Percent complete: 88.1%; Average loss: 2.6815
Iteration: 3526; Percent complete: 88.1%; Average loss: 2.8040
Iteration: 3527; Percent complete: 88.2%; Average loss: 2.7355
Iteration: 3528; Percent complete: 88.2%; Average loss: 2.7022
Iteration: 3529; Percent complete: 88.2%; Average loss: 2.7677
Iteration: 3530; Percent complete: 88.2%; Average loss: 2.9055
Iteration: 3531; Percent complete: 88.3%; Average loss: 2.7678
Iteration: 3532; Percent complete: 88.3%; Average loss: 2.5909
Iteration: 3533; Percent complete: 88.3%; Average loss: 2.8371
Iteration: 3534; Percent complete: 88.3%; Average loss: 2.7569
Iteration: 3535; Percent complete: 88.4%; Average loss: 2.7473
Iteration: 3536; Percent complete: 88.4%; Average loss: 2.9360
Iteration: 3537; Percent complete: 88.4%; Average loss: 2.5389
Iteration: 3538; Percent complete: 88.4%; Average loss: 2.6071
Iteration: 3539; Percent complete: 88.5%; Average loss: 2.8174
Iteration: 3540; Percent complete: 88.5%; Average loss: 2.6913
Iteration: 3541; Percent complete: 88.5%; Average loss: 2.8436
Iteration: 3542; Percent complete: 88.5%; Average loss: 2.5853
Iteration: 3543; Percent complete: 88.6%; Average loss: 2.9336
Iteration: 3544; Percent complete: 88.6%; Average loss: 2.6054
Iteration: 3545; Percent complete: 88.6%; Average loss: 2.8058
Iteration: 3546; Percent complete: 88.6%; Average loss: 2.7299
Iteration: 3547; Percent complete: 88.7%; Average loss: 2.8479
Iteration: 3548; Percent complete: 88.7%; Average loss: 2.9639
Iteration: 3549; Percent complete: 88.7%; Average loss: 2.7946
Iteration: 3550; Percent complete: 88.8%; Average loss: 2.8181
Iteration: 3551; Percent complete: 88.8%; Average loss: 2.8461
Iteration: 3552; Percent complete: 88.8%; Average loss: 2.8302
Iteration: 3553; Percent complete: 88.8%; Average loss: 2.8507
Iteration: 3554; Percent complete: 88.8%; Average loss: 2.8372
Iteration: 3555; Percent complete: 88.9%; Average loss: 2.8896
Iteration: 3556; Percent complete: 88.9%; Average loss: 2.6663
Iteration: 3557; Percent complete: 88.9%; Average loss: 2.6368
Iteration: 3558; Percent complete: 88.9%; Average loss: 2.6175
Iteration: 3559; Percent complete: 89.0%; Average loss: 3.0256
Iteration: 3560; Percent complete: 89.0%; Average loss: 2.7266
Iteration: 3561; Percent complete: 89.0%; Average loss: 2.8076
Iteration: 3562; Percent complete: 89.0%; Average loss: 2.8335
Iteration: 3563; Percent complete: 89.1%; Average loss: 2.8120
Iteration: 3564; Percent complete: 89.1%; Average loss: 2.6551
Iteration: 3565; Percent complete: 89.1%; Average loss: 2.8174
Iteration: 3566; Percent complete: 89.1%; Average loss: 2.7453
Iteration: 3567; Percent complete: 89.2%; Average loss: 2.9482
Iteration: 3568; Percent complete: 89.2%; Average loss: 2.6242
Iteration: 3569; Percent complete: 89.2%; Average loss: 2.7144
Iteration: 3570; Percent complete: 89.2%; Average loss: 2.8574
Iteration: 3571; Percent complete: 89.3%; Average loss: 2.8598
Iteration: 3572; Percent complete: 89.3%; Average loss: 2.7961
Iteration: 3573; Percent complete: 89.3%; Average loss: 3.0146
Iteration: 3574; Percent complete: 89.3%; Average loss: 2.9181
Iteration: 3575; Percent complete: 89.4%; Average loss: 2.7019
Iteration: 3576; Percent complete: 89.4%; Average loss: 2.9525
Iteration: 3577; Percent complete: 89.4%; Average loss: 2.6771
Iteration: 3578; Percent complete: 89.5%; Average loss: 2.7064
Iteration: 3579; Percent complete: 89.5%; Average loss: 2.7057
Iteration: 3580; Percent complete: 89.5%; Average loss: 3.0394
Iteration: 3581; Percent complete: 89.5%; Average loss: 2.7066
Iteration: 3582; Percent complete: 89.5%; Average loss: 2.7936
Iteration: 3583; Percent complete: 89.6%; Average loss: 2.6373
Iteration: 3584; Percent complete: 89.6%; Average loss: 2.7588
Iteration: 3585; Percent complete: 89.6%; Average loss: 2.7752
Iteration: 3586; Percent complete: 89.6%; Average loss: 2.3963
Iteration: 3587; Percent complete: 89.7%; Average loss: 2.7263
Iteration: 3588; Percent complete: 89.7%; Average loss: 2.7067
Iteration: 3589; Percent complete: 89.7%; Average loss: 2.6536
Iteration: 3590; Percent complete: 89.8%; Average loss: 2.6994
Iteration: 3591; Percent complete: 89.8%; Average loss: 2.7088
Iteration: 3592; Percent complete: 89.8%; Average loss: 2.7255
Iteration: 3593; Percent complete: 89.8%; Average loss: 2.7630
Iteration: 3594; Percent complete: 89.8%; Average loss: 2.9216
Iteration: 3595; Percent complete: 89.9%; Average loss: 2.7723
Iteration: 3596; Percent complete: 89.9%; Average loss: 2.9982
Iteration: 3597; Percent complete: 89.9%; Average loss: 2.6163
Iteration: 3598; Percent complete: 90.0%; Average loss: 2.8000
Iteration: 3599; Percent complete: 90.0%; Average loss: 2.7049
Iteration: 3600; Percent complete: 90.0%; Average loss: 2.7661
Iteration: 3601; Percent complete: 90.0%; Average loss: 2.5578
Iteration: 3602; Percent complete: 90.0%; Average loss: 2.5831
Iteration: 3603; Percent complete: 90.1%; Average loss: 2.8103
Iteration: 3604; Percent complete: 90.1%; Average loss: 2.7558
Iteration: 3605; Percent complete: 90.1%; Average loss: 2.7339
Iteration: 3606; Percent complete: 90.1%; Average loss: 2.5987
Iteration: 3607; Percent complete: 90.2%; Average loss: 2.5344
Iteration: 3608; Percent complete: 90.2%; Average loss: 2.5897
Iteration: 3609; Percent complete: 90.2%; Average loss: 2.7184
Iteration: 3610; Percent complete: 90.2%; Average loss: 2.8214
Iteration: 3611; Percent complete: 90.3%; Average loss: 2.9225
Iteration: 3612; Percent complete: 90.3%; Average loss: 2.5892
Iteration: 3613; Percent complete: 90.3%; Average loss: 2.6937
Iteration: 3614; Percent complete: 90.3%; Average loss: 2.6212
Iteration: 3615; Percent complete: 90.4%; Average loss: 2.8098
Iteration: 3616; Percent complete: 90.4%; Average loss: 2.8597
Iteration: 3617; Percent complete: 90.4%; Average loss: 2.8493
Iteration: 3618; Percent complete: 90.5%; Average loss: 2.6951
Iteration: 3619; Percent complete: 90.5%; Average loss: 2.7612
Iteration: 3620; Percent complete: 90.5%; Average loss: 2.6676
Iteration: 3621; Percent complete: 90.5%; Average loss: 2.6652
Iteration: 3622; Percent complete: 90.5%; Average loss: 2.6617
Iteration: 3623; Percent complete: 90.6%; Average loss: 2.6743
Iteration: 3624; Percent complete: 90.6%; Average loss: 2.9828
Iteration: 3625; Percent complete: 90.6%; Average loss: 2.6892
Iteration: 3626; Percent complete: 90.6%; Average loss: 2.5996
Iteration: 3627; Percent complete: 90.7%; Average loss: 2.8204
Iteration: 3628; Percent complete: 90.7%; Average loss: 2.6394
Iteration: 3629; Percent complete: 90.7%; Average loss: 2.7015
Iteration: 3630; Percent complete: 90.8%; Average loss: 2.6034
Iteration: 3631; Percent complete: 90.8%; Average loss: 2.6851
Iteration: 3632; Percent complete: 90.8%; Average loss: 2.6222
Iteration: 3633; Percent complete: 90.8%; Average loss: 2.4610
Iteration: 3634; Percent complete: 90.8%; Average loss: 2.8211
Iteration: 3635; Percent complete: 90.9%; Average loss: 2.8777
Iteration: 3636; Percent complete: 90.9%; Average loss: 2.6856
Iteration: 3637; Percent complete: 90.9%; Average loss: 2.6526
Iteration: 3638; Percent complete: 91.0%; Average loss: 2.8967
Iteration: 3639; Percent complete: 91.0%; Average loss: 2.8170
Iteration: 3640; Percent complete: 91.0%; Average loss: 2.7540
Iteration: 3641; Percent complete: 91.0%; Average loss: 2.6387
Iteration: 3642; Percent complete: 91.0%; Average loss: 2.6843
Iteration: 3643; Percent complete: 91.1%; Average loss: 2.7913
Iteration: 3644; Percent complete: 91.1%; Average loss: 2.6292
Iteration: 3645; Percent complete: 91.1%; Average loss: 2.8574
Iteration: 3646; Percent complete: 91.1%; Average loss: 2.5092
Iteration: 3647; Percent complete: 91.2%; Average loss: 2.6092
Iteration: 3648; Percent complete: 91.2%; Average loss: 2.7760
Iteration: 3649; Percent complete: 91.2%; Average loss: 2.8272
Iteration: 3650; Percent complete: 91.2%; Average loss: 2.5230
Iteration: 3651; Percent complete: 91.3%; Average loss: 2.9044
Iteration: 3652; Percent complete: 91.3%; Average loss: 2.8707
Iteration: 3653; Percent complete: 91.3%; Average loss: 2.7707
Iteration: 3654; Percent complete: 91.3%; Average loss: 2.5273
Iteration: 3655; Percent complete: 91.4%; Average loss: 2.5943
Iteration: 3656; Percent complete: 91.4%; Average loss: 2.7156
Iteration: 3657; Percent complete: 91.4%; Average loss: 2.4324
Iteration: 3658; Percent complete: 91.5%; Average loss: 2.8833
Iteration: 3659; Percent complete: 91.5%; Average loss: 2.5700
Iteration: 3660; Percent complete: 91.5%; Average loss: 2.5888
Iteration: 3661; Percent complete: 91.5%; Average loss: 2.8127
Iteration: 3662; Percent complete: 91.5%; Average loss: 2.5522
Iteration: 3663; Percent complete: 91.6%; Average loss: 2.6647
Iteration: 3664; Percent complete: 91.6%; Average loss: 2.7204
Iteration: 3665; Percent complete: 91.6%; Average loss: 2.7960
Iteration: 3666; Percent complete: 91.6%; Average loss: 2.8768
Iteration: 3667; Percent complete: 91.7%; Average loss: 2.7416
Iteration: 3668; Percent complete: 91.7%; Average loss: 2.5861
Iteration: 3669; Percent complete: 91.7%; Average loss: 2.6399
Iteration: 3670; Percent complete: 91.8%; Average loss: 2.5586
Iteration: 3671; Percent complete: 91.8%; Average loss: 2.6799
Iteration: 3672; Percent complete: 91.8%; Average loss: 2.6976
Iteration: 3673; Percent complete: 91.8%; Average loss: 2.8845
Iteration: 3674; Percent complete: 91.8%; Average loss: 2.7324
Iteration: 3675; Percent complete: 91.9%; Average loss: 2.8760
Iteration: 3676; Percent complete: 91.9%; Average loss: 2.6366
Iteration: 3677; Percent complete: 91.9%; Average loss: 2.8472
Iteration: 3678; Percent complete: 92.0%; Average loss: 2.6183
Iteration: 3679; Percent complete: 92.0%; Average loss: 2.6286
Iteration: 3680; Percent complete: 92.0%; Average loss: 2.7831
Iteration: 3681; Percent complete: 92.0%; Average loss: 2.6663
Iteration: 3682; Percent complete: 92.0%; Average loss: 2.8263
Iteration: 3683; Percent complete: 92.1%; Average loss: 2.6867
Iteration: 3684; Percent complete: 92.1%; Average loss: 2.7231
Iteration: 3685; Percent complete: 92.1%; Average loss: 2.8204
Iteration: 3686; Percent complete: 92.2%; Average loss: 2.7456
Iteration: 3687; Percent complete: 92.2%; Average loss: 2.8229
Iteration: 3688; Percent complete: 92.2%; Average loss: 2.7821
Iteration: 3689; Percent complete: 92.2%; Average loss: 2.6971
Iteration: 3690; Percent complete: 92.2%; Average loss: 2.5504
Iteration: 3691; Percent complete: 92.3%; Average loss: 2.8867
Iteration: 3692; Percent complete: 92.3%; Average loss: 2.7255
Iteration: 3693; Percent complete: 92.3%; Average loss: 2.7363
Iteration: 3694; Percent complete: 92.3%; Average loss: 2.6669
Iteration: 3695; Percent complete: 92.4%; Average loss: 2.6874
Iteration: 3696; Percent complete: 92.4%; Average loss: 2.7461
Iteration: 3697; Percent complete: 92.4%; Average loss: 2.5584
Iteration: 3698; Percent complete: 92.5%; Average loss: 2.9733
Iteration: 3699; Percent complete: 92.5%; Average loss: 2.6370
Iteration: 3700; Percent complete: 92.5%; Average loss: 2.4998
Iteration: 3701; Percent complete: 92.5%; Average loss: 2.8413
Iteration: 3702; Percent complete: 92.5%; Average loss: 2.5378
Iteration: 3703; Percent complete: 92.6%; Average loss: 2.6494
Iteration: 3704; Percent complete: 92.6%; Average loss: 2.9082
Iteration: 3705; Percent complete: 92.6%; Average loss: 2.8530
Iteration: 3706; Percent complete: 92.7%; Average loss: 2.7594
Iteration: 3707; Percent complete: 92.7%; Average loss: 2.6966
Iteration: 3708; Percent complete: 92.7%; Average loss: 2.8303
Iteration: 3709; Percent complete: 92.7%; Average loss: 2.4203
Iteration: 3710; Percent complete: 92.8%; Average loss: 2.6433
Iteration: 3711; Percent complete: 92.8%; Average loss: 2.6872
Iteration: 3712; Percent complete: 92.8%; Average loss: 2.6892
Iteration: 3713; Percent complete: 92.8%; Average loss: 2.7012
Iteration: 3714; Percent complete: 92.8%; Average loss: 2.6010
Iteration: 3715; Percent complete: 92.9%; Average loss: 2.7396
Iteration: 3716; Percent complete: 92.9%; Average loss: 2.5166
Iteration: 3717; Percent complete: 92.9%; Average loss: 2.7851
Iteration: 3718; Percent complete: 93.0%; Average loss: 2.6893
Iteration: 3719; Percent complete: 93.0%; Average loss: 2.7553
Iteration: 3720; Percent complete: 93.0%; Average loss: 2.5084
Iteration: 3721; Percent complete: 93.0%; Average loss: 2.7259
Iteration: 3722; Percent complete: 93.0%; Average loss: 2.6782
Iteration: 3723; Percent complete: 93.1%; Average loss: 2.4210
Iteration: 3724; Percent complete: 93.1%; Average loss: 2.5899
Iteration: 3725; Percent complete: 93.1%; Average loss: 2.5027
Iteration: 3726; Percent complete: 93.2%; Average loss: 2.7132
Iteration: 3727; Percent complete: 93.2%; Average loss: 2.6184
Iteration: 3728; Percent complete: 93.2%; Average loss: 2.7063
Iteration: 3729; Percent complete: 93.2%; Average loss: 2.7719
Iteration: 3730; Percent complete: 93.2%; Average loss: 2.7692
Iteration: 3731; Percent complete: 93.3%; Average loss: 2.8248
Iteration: 3732; Percent complete: 93.3%; Average loss: 2.8897
Iteration: 3733; Percent complete: 93.3%; Average loss: 2.9183
Iteration: 3734; Percent complete: 93.3%; Average loss: 2.7507
Iteration: 3735; Percent complete: 93.4%; Average loss: 2.6958
Iteration: 3736; Percent complete: 93.4%; Average loss: 2.6657
Iteration: 3737; Percent complete: 93.4%; Average loss: 2.6662
Iteration: 3738; Percent complete: 93.5%; Average loss: 2.5975
Iteration: 3739; Percent complete: 93.5%; Average loss: 2.6774
Iteration: 3740; Percent complete: 93.5%; Average loss: 2.6525
Iteration: 3741; Percent complete: 93.5%; Average loss: 2.9856
Iteration: 3742; Percent complete: 93.5%; Average loss: 2.8331
Iteration: 3743; Percent complete: 93.6%; Average loss: 2.6998
Iteration: 3744; Percent complete: 93.6%; Average loss: 2.8396
Iteration: 3745; Percent complete: 93.6%; Average loss: 2.8953
Iteration: 3746; Percent complete: 93.7%; Average loss: 3.0537
Iteration: 3747; Percent complete: 93.7%; Average loss: 2.7079
Iteration: 3748; Percent complete: 93.7%; Average loss: 2.7028
Iteration: 3749; Percent complete: 93.7%; Average loss: 2.6947
Iteration: 3750; Percent complete: 93.8%; Average loss: 2.5450
Iteration: 3751; Percent complete: 93.8%; Average loss: 2.6939
Iteration: 3752; Percent complete: 93.8%; Average loss: 2.4647
Iteration: 3753; Percent complete: 93.8%; Average loss: 2.5910
Iteration: 3754; Percent complete: 93.8%; Average loss: 2.7035
Iteration: 3755; Percent complete: 93.9%; Average loss: 2.5973
Iteration: 3756; Percent complete: 93.9%; Average loss: 2.6020
Iteration: 3757; Percent complete: 93.9%; Average loss: 2.6250
Iteration: 3758; Percent complete: 94.0%; Average loss: 2.5198
Iteration: 3759; Percent complete: 94.0%; Average loss: 2.5873
Iteration: 3760; Percent complete: 94.0%; Average loss: 2.6990
Iteration: 3761; Percent complete: 94.0%; Average loss: 2.7470
Iteration: 3762; Percent complete: 94.0%; Average loss: 2.7480
Iteration: 3763; Percent complete: 94.1%; Average loss: 2.6125
Iteration: 3764; Percent complete: 94.1%; Average loss: 2.5601
Iteration: 3765; Percent complete: 94.1%; Average loss: 2.8166
Iteration: 3766; Percent complete: 94.2%; Average loss: 2.6972
Iteration: 3767; Percent complete: 94.2%; Average loss: 2.8961
Iteration: 3768; Percent complete: 94.2%; Average loss: 2.7825
Iteration: 3769; Percent complete: 94.2%; Average loss: 2.5310
Iteration: 3770; Percent complete: 94.2%; Average loss: 2.8818
Iteration: 3771; Percent complete: 94.3%; Average loss: 2.6336
Iteration: 3772; Percent complete: 94.3%; Average loss: 2.7304
Iteration: 3773; Percent complete: 94.3%; Average loss: 2.5962
Iteration: 3774; Percent complete: 94.3%; Average loss: 2.5469
Iteration: 3775; Percent complete: 94.4%; Average loss: 2.5674
Iteration: 3776; Percent complete: 94.4%; Average loss: 2.7029
Iteration: 3777; Percent complete: 94.4%; Average loss: 2.8998
Iteration: 3778; Percent complete: 94.5%; Average loss: 2.5176
Iteration: 3779; Percent complete: 94.5%; Average loss: 2.6521
Iteration: 3780; Percent complete: 94.5%; Average loss: 2.5593
Iteration: 3781; Percent complete: 94.5%; Average loss: 2.6503
Iteration: 3782; Percent complete: 94.5%; Average loss: 2.4736
Iteration: 3783; Percent complete: 94.6%; Average loss: 2.5971
Iteration: 3784; Percent complete: 94.6%; Average loss: 2.7624
Iteration: 3785; Percent complete: 94.6%; Average loss: 2.6752
Iteration: 3786; Percent complete: 94.7%; Average loss: 2.4017
Iteration: 3787; Percent complete: 94.7%; Average loss: 2.6797
Iteration: 3788; Percent complete: 94.7%; Average loss: 2.6742
Iteration: 3789; Percent complete: 94.7%; Average loss: 2.5722
Iteration: 3790; Percent complete: 94.8%; Average loss: 2.6223
Iteration: 3791; Percent complete: 94.8%; Average loss: 2.6715
Iteration: 3792; Percent complete: 94.8%; Average loss: 2.5994
Iteration: 3793; Percent complete: 94.8%; Average loss: 2.8838
Iteration: 3794; Percent complete: 94.8%; Average loss: 2.8467
Iteration: 3795; Percent complete: 94.9%; Average loss: 2.6484
Iteration: 3796; Percent complete: 94.9%; Average loss: 2.4074
Iteration: 3797; Percent complete: 94.9%; Average loss: 2.4788
Iteration: 3798; Percent complete: 95.0%; Average loss: 2.9314
Iteration: 3799; Percent complete: 95.0%; Average loss: 2.5468
Iteration: 3800; Percent complete: 95.0%; Average loss: 2.7148
Iteration: 3801; Percent complete: 95.0%; Average loss: 2.6854
Iteration: 3802; Percent complete: 95.0%; Average loss: 2.6875
Iteration: 3803; Percent complete: 95.1%; Average loss: 2.8216
Iteration: 3804; Percent complete: 95.1%; Average loss: 2.6136
Iteration: 3805; Percent complete: 95.1%; Average loss: 2.5873
Iteration: 3806; Percent complete: 95.2%; Average loss: 2.5796
Iteration: 3807; Percent complete: 95.2%; Average loss: 2.6158
Iteration: 3808; Percent complete: 95.2%; Average loss: 2.5960
Iteration: 3809; Percent complete: 95.2%; Average loss: 2.7143
Iteration: 3810; Percent complete: 95.2%; Average loss: 2.5998
Iteration: 3811; Percent complete: 95.3%; Average loss: 2.5175
Iteration: 3812; Percent complete: 95.3%; Average loss: 2.7244
Iteration: 3813; Percent complete: 95.3%; Average loss: 2.6033
Iteration: 3814; Percent complete: 95.3%; Average loss: 2.7163
Iteration: 3815; Percent complete: 95.4%; Average loss: 2.4727
Iteration: 3816; Percent complete: 95.4%; Average loss: 2.3860
Iteration: 3817; Percent complete: 95.4%; Average loss: 2.8424
Iteration: 3818; Percent complete: 95.5%; Average loss: 2.7467
Iteration: 3819; Percent complete: 95.5%; Average loss: 2.4449
Iteration: 3820; Percent complete: 95.5%; Average loss: 2.6365
Iteration: 3821; Percent complete: 95.5%; Average loss: 2.7260
Iteration: 3822; Percent complete: 95.5%; Average loss: 2.8854
Iteration: 3823; Percent complete: 95.6%; Average loss: 2.8091
Iteration: 3824; Percent complete: 95.6%; Average loss: 2.6497
Iteration: 3825; Percent complete: 95.6%; Average loss: 2.6194
Iteration: 3826; Percent complete: 95.7%; Average loss: 2.6596
Iteration: 3827; Percent complete: 95.7%; Average loss: 2.6622
Iteration: 3828; Percent complete: 95.7%; Average loss: 2.7298
Iteration: 3829; Percent complete: 95.7%; Average loss: 2.5951
Iteration: 3830; Percent complete: 95.8%; Average loss: 2.5278
Iteration: 3831; Percent complete: 95.8%; Average loss: 2.5030
Iteration: 3832; Percent complete: 95.8%; Average loss: 2.5677
Iteration: 3833; Percent complete: 95.8%; Average loss: 2.6887
Iteration: 3834; Percent complete: 95.9%; Average loss: 2.6531
Iteration: 3835; Percent complete: 95.9%; Average loss: 2.6936
Iteration: 3836; Percent complete: 95.9%; Average loss: 2.7403
Iteration: 3837; Percent complete: 95.9%; Average loss: 2.5809
Iteration: 3838; Percent complete: 96.0%; Average loss: 2.5497
Iteration: 3839; Percent complete: 96.0%; Average loss: 2.6738
Iteration: 3840; Percent complete: 96.0%; Average loss: 2.7550
Iteration: 3841; Percent complete: 96.0%; Average loss: 2.6702
Iteration: 3842; Percent complete: 96.0%; Average loss: 2.5783
Iteration: 3843; Percent complete: 96.1%; Average loss: 2.8931
Iteration: 3844; Percent complete: 96.1%; Average loss: 2.7730
Iteration: 3845; Percent complete: 96.1%; Average loss: 2.6961
Iteration: 3846; Percent complete: 96.2%; Average loss: 2.5907
Iteration: 3847; Percent complete: 96.2%; Average loss: 2.5017
Iteration: 3848; Percent complete: 96.2%; Average loss: 2.9108
Iteration: 3849; Percent complete: 96.2%; Average loss: 2.8639
Iteration: 3850; Percent complete: 96.2%; Average loss: 2.5408
Iteration: 3851; Percent complete: 96.3%; Average loss: 2.6491
Iteration: 3852; Percent complete: 96.3%; Average loss: 2.6769
Iteration: 3853; Percent complete: 96.3%; Average loss: 2.4876
Iteration: 3854; Percent complete: 96.4%; Average loss: 2.7811
Iteration: 3855; Percent complete: 96.4%; Average loss: 2.6794
Iteration: 3856; Percent complete: 96.4%; Average loss: 2.6608
Iteration: 3857; Percent complete: 96.4%; Average loss: 2.7207
Iteration: 3858; Percent complete: 96.5%; Average loss: 2.6864
Iteration: 3859; Percent complete: 96.5%; Average loss: 2.5426
Iteration: 3860; Percent complete: 96.5%; Average loss: 2.7114
Iteration: 3861; Percent complete: 96.5%; Average loss: 2.6169
Iteration: 3862; Percent complete: 96.5%; Average loss: 2.5764
Iteration: 3863; Percent complete: 96.6%; Average loss: 2.5227
Iteration: 3864; Percent complete: 96.6%; Average loss: 2.5068
Iteration: 3865; Percent complete: 96.6%; Average loss: 2.5788
Iteration: 3866; Percent complete: 96.7%; Average loss: 2.6561
Iteration: 3867; Percent complete: 96.7%; Average loss: 2.6058
Iteration: 3868; Percent complete: 96.7%; Average loss: 2.9585
Iteration: 3869; Percent complete: 96.7%; Average loss: 2.6924
Iteration: 3870; Percent complete: 96.8%; Average loss: 2.6295
Iteration: 3871; Percent complete: 96.8%; Average loss: 2.7079
Iteration: 3872; Percent complete: 96.8%; Average loss: 2.9232
Iteration: 3873; Percent complete: 96.8%; Average loss: 2.5249
Iteration: 3874; Percent complete: 96.9%; Average loss: 2.5902
Iteration: 3875; Percent complete: 96.9%; Average loss: 2.5693
Iteration: 3876; Percent complete: 96.9%; Average loss: 2.8511
Iteration: 3877; Percent complete: 96.9%; Average loss: 2.5115
Iteration: 3878; Percent complete: 97.0%; Average loss: 2.6811
Iteration: 3879; Percent complete: 97.0%; Average loss: 2.5823
Iteration: 3880; Percent complete: 97.0%; Average loss: 2.5969
Iteration: 3881; Percent complete: 97.0%; Average loss: 2.9334
Iteration: 3882; Percent complete: 97.0%; Average loss: 2.6132
Iteration: 3883; Percent complete: 97.1%; Average loss: 2.6212
Iteration: 3884; Percent complete: 97.1%; Average loss: 2.6246
Iteration: 3885; Percent complete: 97.1%; Average loss: 2.6773
Iteration: 3886; Percent complete: 97.2%; Average loss: 2.7836
Iteration: 3887; Percent complete: 97.2%; Average loss: 2.6191
Iteration: 3888; Percent complete: 97.2%; Average loss: 2.4874
Iteration: 3889; Percent complete: 97.2%; Average loss: 2.6006
Iteration: 3890; Percent complete: 97.2%; Average loss: 2.8118
Iteration: 3891; Percent complete: 97.3%; Average loss: 2.7325
Iteration: 3892; Percent complete: 97.3%; Average loss: 2.7200
Iteration: 3893; Percent complete: 97.3%; Average loss: 2.6919
Iteration: 3894; Percent complete: 97.4%; Average loss: 2.5524
Iteration: 3895; Percent complete: 97.4%; Average loss: 2.6946
Iteration: 3896; Percent complete: 97.4%; Average loss: 2.7621
Iteration: 3897; Percent complete: 97.4%; Average loss: 2.7346
Iteration: 3898; Percent complete: 97.5%; Average loss: 2.7469
Iteration: 3899; Percent complete: 97.5%; Average loss: 2.5846
Iteration: 3900; Percent complete: 97.5%; Average loss: 2.4757
Iteration: 3901; Percent complete: 97.5%; Average loss: 2.8625
Iteration: 3902; Percent complete: 97.5%; Average loss: 2.6366
Iteration: 3903; Percent complete: 97.6%; Average loss: 2.6153
Iteration: 3904; Percent complete: 97.6%; Average loss: 2.4437
Iteration: 3905; Percent complete: 97.6%; Average loss: 2.5991
Iteration: 3906; Percent complete: 97.7%; Average loss: 2.5352
Iteration: 3907; Percent complete: 97.7%; Average loss: 2.6359
Iteration: 3908; Percent complete: 97.7%; Average loss: 2.7867
Iteration: 3909; Percent complete: 97.7%; Average loss: 2.6505
Iteration: 3910; Percent complete: 97.8%; Average loss: 2.4799
Iteration: 3911; Percent complete: 97.8%; Average loss: 2.7178
Iteration: 3912; Percent complete: 97.8%; Average loss: 2.6678
Iteration: 3913; Percent complete: 97.8%; Average loss: 2.7271
Iteration: 3914; Percent complete: 97.9%; Average loss: 2.4463
Iteration: 3915; Percent complete: 97.9%; Average loss: 2.5956
Iteration: 3916; Percent complete: 97.9%; Average loss: 2.3963
Iteration: 3917; Percent complete: 97.9%; Average loss: 2.6470
Iteration: 3918; Percent complete: 98.0%; Average loss: 2.5366
Iteration: 3919; Percent complete: 98.0%; Average loss: 2.6122
Iteration: 3920; Percent complete: 98.0%; Average loss: 2.7600
Iteration: 3921; Percent complete: 98.0%; Average loss: 2.8265
Iteration: 3922; Percent complete: 98.0%; Average loss: 2.5236
Iteration: 3923; Percent complete: 98.1%; Average loss: 2.8251
Iteration: 3924; Percent complete: 98.1%; Average loss: 2.8183
Iteration: 3925; Percent complete: 98.1%; Average loss: 2.4824
Iteration: 3926; Percent complete: 98.2%; Average loss: 2.6572
Iteration: 3927; Percent complete: 98.2%; Average loss: 2.6069
Iteration: 3928; Percent complete: 98.2%; Average loss: 2.5718
Iteration: 3929; Percent complete: 98.2%; Average loss: 2.6386
Iteration: 3930; Percent complete: 98.2%; Average loss: 2.6685
Iteration: 3931; Percent complete: 98.3%; Average loss: 2.7963
Iteration: 3932; Percent complete: 98.3%; Average loss: 2.5427
Iteration: 3933; Percent complete: 98.3%; Average loss: 2.7208
Iteration: 3934; Percent complete: 98.4%; Average loss: 3.1479
Iteration: 3935; Percent complete: 98.4%; Average loss: 2.6268
Iteration: 3936; Percent complete: 98.4%; Average loss: 2.6212
Iteration: 3937; Percent complete: 98.4%; Average loss: 2.5660
Iteration: 3938; Percent complete: 98.5%; Average loss: 2.5752
Iteration: 3939; Percent complete: 98.5%; Average loss: 2.5611
Iteration: 3940; Percent complete: 98.5%; Average loss: 2.7212
Iteration: 3941; Percent complete: 98.5%; Average loss: 2.7245
Iteration: 3942; Percent complete: 98.6%; Average loss: 2.7160
Iteration: 3943; Percent complete: 98.6%; Average loss: 2.5187
Iteration: 3944; Percent complete: 98.6%; Average loss: 2.5629
Iteration: 3945; Percent complete: 98.6%; Average loss: 2.5491
Iteration: 3946; Percent complete: 98.7%; Average loss: 2.5727
Iteration: 3947; Percent complete: 98.7%; Average loss: 2.5268
Iteration: 3948; Percent complete: 98.7%; Average loss: 2.6187
Iteration: 3949; Percent complete: 98.7%; Average loss: 2.6880
Iteration: 3950; Percent complete: 98.8%; Average loss: 2.7497
Iteration: 3951; Percent complete: 98.8%; Average loss: 2.4970
Iteration: 3952; Percent complete: 98.8%; Average loss: 2.7791
Iteration: 3953; Percent complete: 98.8%; Average loss: 2.6909
Iteration: 3954; Percent complete: 98.9%; Average loss: 2.8533
Iteration: 3955; Percent complete: 98.9%; Average loss: 2.5428
Iteration: 3956; Percent complete: 98.9%; Average loss: 2.4846
Iteration: 3957; Percent complete: 98.9%; Average loss: 2.7479
Iteration: 3958; Percent complete: 99.0%; Average loss: 2.4037
Iteration: 3959; Percent complete: 99.0%; Average loss: 2.6158
Iteration: 3960; Percent complete: 99.0%; Average loss: 2.6414
Iteration: 3961; Percent complete: 99.0%; Average loss: 2.6526
Iteration: 3962; Percent complete: 99.1%; Average loss: 2.8256
Iteration: 3963; Percent complete: 99.1%; Average loss: 2.6865
Iteration: 3964; Percent complete: 99.1%; Average loss: 2.5760
Iteration: 3965; Percent complete: 99.1%; Average loss: 2.6795
Iteration: 3966; Percent complete: 99.2%; Average loss: 2.7059
Iteration: 3967; Percent complete: 99.2%; Average loss: 2.7938
Iteration: 3968; Percent complete: 99.2%; Average loss: 2.4644
Iteration: 3969; Percent complete: 99.2%; Average loss: 2.3942
Iteration: 3970; Percent complete: 99.2%; Average loss: 2.4838
Iteration: 3971; Percent complete: 99.3%; Average loss: 2.8357
Iteration: 3972; Percent complete: 99.3%; Average loss: 2.7246
Iteration: 3973; Percent complete: 99.3%; Average loss: 2.7076
Iteration: 3974; Percent complete: 99.4%; Average loss: 2.5237
Iteration: 3975; Percent complete: 99.4%; Average loss: 2.9001
Iteration: 3976; Percent complete: 99.4%; Average loss: 2.7098
Iteration: 3977; Percent complete: 99.4%; Average loss: 2.7858
Iteration: 3978; Percent complete: 99.5%; Average loss: 2.5561
Iteration: 3979; Percent complete: 99.5%; Average loss: 2.5108
Iteration: 3980; Percent complete: 99.5%; Average loss: 2.4073
Iteration: 3981; Percent complete: 99.5%; Average loss: 2.6414
Iteration: 3982; Percent complete: 99.6%; Average loss: 2.3751
Iteration: 3983; Percent complete: 99.6%; Average loss: 2.6773
Iteration: 3984; Percent complete: 99.6%; Average loss: 2.5423
Iteration: 3985; Percent complete: 99.6%; Average loss: 2.5468
Iteration: 3986; Percent complete: 99.7%; Average loss: 2.8059
Iteration: 3987; Percent complete: 99.7%; Average loss: 2.3426
Iteration: 3988; Percent complete: 99.7%; Average loss: 2.7404
Iteration: 3989; Percent complete: 99.7%; Average loss: 2.6151
Iteration: 3990; Percent complete: 99.8%; Average loss: 2.4174
Iteration: 3991; Percent complete: 99.8%; Average loss: 2.6785
Iteration: 3992; Percent complete: 99.8%; Average loss: 2.6684
Iteration: 3993; Percent complete: 99.8%; Average loss: 2.6111
Iteration: 3994; Percent complete: 99.9%; Average loss: 2.7742
Iteration: 3995; Percent complete: 99.9%; Average loss: 2.5143
Iteration: 3996; Percent complete: 99.9%; Average loss: 2.5743
Iteration: 3997; Percent complete: 99.9%; Average loss: 2.4360
Iteration: 3998; Percent complete: 100.0%; Average loss: 2.7762
Iteration: 3999; Percent complete: 100.0%; Average loss: 2.6665
Iteration: 4000; Percent complete: 100.0%; Average loss: 2.8545

평가 수행하기

여러분의 모델과 채팅을 해보고 싶다면 다음 블록을 수행하면 됩니다.

# Dropout 레이어를 평가( ``eval`` ) 모드로 설정합니다
encoder.eval()
decoder.eval()

# 탐색 모듈을 초기화합니다
searcher = GreedySearchDecoder(encoder, decoder)

# 채팅을 시작합니다 (다음 줄의 주석을 제거하면 시작해볼 수 있습니다)
# evaluateInput(encoder, decoder, searcher, voc)

맺음말

이번 튜토리얼을 이것으로 마무리하겠습니다. 축하합니다! 여러분은 이제 생성 챗봇 모델을 만들기 위한 기초 지식을 습득했습니다. 만약 좀 더 관심이 있다면 모델이나 학습 매개변수를 수정해 보면서, 혹은 모델을 학습할 데이터를 바꿔 보면서 챗봇의 행동을 수정해볼 수 있을 것입니다.

그 외에도 딥러닝의 멋진 활용 예에 대한 PyTorch 튜토리얼이 있으니 한 번 확인해 보기 바랍니다!